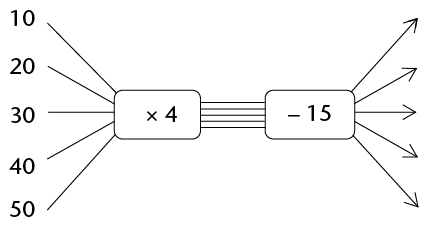
Complete the flow diagram.
5.3 Using flow diagrams and tables
A relationship between two quantities can be shown using a flow diagram such as the one below. Each input number in a flow diagram has a corresponding output number. The first (top) input number corresponds to the first output number. The second input number corresponds to the second output number, and so on.

For example, in the flow diagram above, the output number, \(8\), corresponds to the input number, \(3\), and the input number, \(–1\), corresponds to the output number, \(4\).
\(3 + 5 = 8\) and \(- 1 + 5 = 4\)
We call \(+5\) the \(operator\) (or \(function\)). It tells you what happens to the input number to get to the output number.
Worked Example 5.3: Completing flow diagrams
Complete this flow diagram.
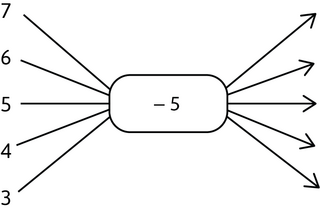
Identify the operator (or the function).
The operator is \(-5\), so we need to subtract \(5\) from the input numbers to get the output numbers.
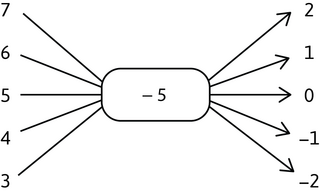
Find the output numbers.
\[\begin{align} 7 - 5 &= 2 \\ 6 - 5 &= 1 \\ 5 - 5 &= 0 \\ 4 - 5 &= - 1 \\ 3 - 5 &= - 2 \end{align}\]Complete the flow diagram.
Sometimes more than one calculation is required to find the output number.
Worked Example 5.4: Completing flow diagrams
Complete this flow diagram.
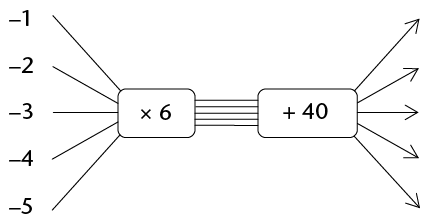
Identify the operator.
In this case, we have two operators that follow each other: \(\times 6\) followed by \(+ 40\), so we need to multiply the input numbers by \(6\) and then add \(40\) to get the output numbers.
Find the output numbers.
\[\begin{align} - 1 \times 6 + 40 &= - 6 + 40 = 34 \\ - 2 \times 6 + 40 &= - 12 + 40 = 28 \\ - 3 \times 6 + 40 &= - 18 + 40 = 22 \\ - 4 \times 6 + 40 &= - 24 + 40 = 16 \\ - 5 \times 6 + 40 &= - 30 + 40 = 10 \end{align}\]Complete the flow diagram.
Complete the flow diagram.
Complete the flow diagram.
Use the flow diagram to complete the table.

| Input number | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
| Output number |
| Input number | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
| Output number | \(200\) | \(250\) | \(300\) | \(350\) | \(400\) | \(450\) |
Use the flow diagram to complete the table.

| Input number | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
| Output number |
| Input number | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |
| Output number | \(65\) | \(115\) | \(165\) | \(215\) | \(265\) | \(315\) |
A completed flow diagram shows two kinds of information:
- the calculations that are done to produce the output numbers
- which output number is connected to which input number.
The flow diagram that you have completed in Worked example 5.4 shows the following information:

Each input number is multiplied by \(6\), then \(40\) is added to produce the output numbers.
The input and output numbers are connected as shown in the table below.
| Input numbers | \(−1\) | \(−2\) | \(−3\) | \(−4\) | \(−5\) |
| Output numbers | \(34\) | \(28\) | \(22\) | \(16\) | \(10\) |
We can say that the rule is: \(\text{input number } \times 6 + 40\)
So, we can describe the output number like this:
\[\text{output number } = \text{ input number } \times 6 + 40\]We call this type of calculation a formula. A formula is also an equation, which shows how the amounts are related to each other.
- formula
- a mathematical relationship or rule expressed in numbers and letters
- equation
- a statement of how two mathematical expressions are equal
Instead of writing “input number” and “output number” in formulas, we can just write a single letter symbol as an abbreviation.
Long ago, mathematicians started to use the convention of using the letter symbol \(x\) as an abbreviation for the input number, and the letter symbol \(y\) as an abbreviation for the output number.
So, for example, we can write the formula above as \(y = x \times 6 + 40\), where \(y\) is the output number and \(x\) is the input number. In a more compact way, we write this as \(y = 6x + 40\).
Letter symbols other than \(x\) and \(y\) can also be used to indicate these quantities.
A table of values lists two groups of numbers: the input values (or \(x\)) in the top row and the output values (or \(y\)) in the bottom row. The numbers that are above and below each other are related to each other by the equation.
Worked Example 5.5: Using tables and formulae
The table below shows input and output values for the equation \(y = 5x + 3\).
| \(x\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y\) | \(18\) | \(23\) | \(28\) | \(33\) |
- What is the output for the input value of \(4\)?
- Which input led to the output value of \(28\)?
- If the input is \(x = 1\), what is the output \(y\) value?
Look at the table of values to find the output value for the input value of \(4\).
Reading the table of values: if \(x = 4\), then \(y = 23\). The number \(23\) (output) is directly below the number \(4\) (input). Check the answer using the given formula:
\[y = 5x + 3\]so
\[\begin{align} y &= 5(4) + 3 \\ &= 20 + 3 \\ &= 23 \end{align}\]Find the input value that led to the output value of \(28\).
Reading the table of values: if \(y = 28\), then \(x = 5\). The number \(5\) (input) is directly above the number \(28\) (output). Check the answer using the given formula:
\[\begin{align} 28 &= 5(x) + 3 \\ 28 &= 5(5) + 3 \\ 28 &= 25 + 3 \\ 28 &= 28 \end{align}\]Find the output value of \(y\) for the input value \(x = 1\).
The input \(x = 1\) is not in the given table. We have a formula, so we can use it to find the output.
\[\begin{align} y &= 5(x) + 3 \\ y &= 5(1) + 3 \\ y &= 5 + 3 = 8 \end{align}\]So, if \(x = 1\), then \(y = 8\).
Note how we simply replace \(x\) and \(y\) in the formula with the given numbers.
Worked Example 5.6: Using flow diagrams and formulae
This flow diagram shows some inputs and outputs for the equation \(y = 5x + 3\).
- What is the output for the input value of \(3\)?
- Which input led to the output value of \(33\)?
- If the input is \(x = 2\), what is the output \(y\) value?
Find the output value for the input value of \(3\).
From the flow diagram, we read left to right to find the output: if the input is \(3\), then the output is \(18\).
Find the input value that led to the output value of \(33\).
From the flow diagram, we read right to left to find the input: if the output is \(33\), then the input is \(6\).
Find the output value of \(y\) for the input value \(x = 2\).
The input \(x = 2\) is not in the given flow diagram. We have a formula, so we can use it to find the output.
\[\begin{align} y &= 5(x) + 3 \\ y &= 5(2) + 3 \\ y &= 10 + 3 = 13 \end{align}\]So, if \(x = 2\), then \(y = 13\).
