In Chapter 5, you already learnt how to complete tables using equations and how to read flow diagrams to
analyse different functions and relationships. We will now look at more examples of using an equation to
complete a table of values. Remember, the table of values can help you to sketch graphs and look for patterns in
a relationship.
When working with integers, pay a special attention to operations with negative numbers. For example, when
you need to substitute \(x = - 10\) into the equation \(y = x^{2}\), make sure you use brackets around the
input value:
\[\begin{align}
y &= ( - 10)^{2} \\
&= 100
\end{align}\]
If the relationship has fractions and integers, look out for any sign change after substituting a negative
number in the numerator or denominator. For example, if \(x = - 2\) and \(y = - \frac{2x}{6}\), then
\[\begin{align}
y &= - \frac{2( - 2)}{6} \\
&= - \frac{- 4}{6} \\
&= - \left( - \frac{2}{3} \right) \\
&= + \frac{2}{3} \\
&= \frac{2}{3}
\end{align}\]
Worked Example 21.1: Using equations to complete
tables
Fill in the table of values below for the equation, \(y = - \frac{x}{2} - 1\).
| \(x\) |
\(−6\) |
\(−4\) |
\(−2\) |
\(−1\) |
\(1\) |
\(6\) |
| \(y\) |
\(2\) |
\(1\) |
\(0\) |
|
|
\(−4\) |
Use the equation to find the first missing number.
The input for the first missing number is \(x = - 1\). Substitute this value into the given equation:
\[\begin{align}
y &= - \frac{x}{2} - 1 \\
y &= - \frac{(- 1)}{2} - 1 \\
y &= + \frac{1}{2} - 1 \\
y &= - \frac{1}{2}
\end{align}\]
So, the first missing value is \(- \frac{1}{2}\).
Use the equation to find the second missing
number.
The input for the second missing number is \(x = 1\). Substitute this value into the given equation:
\[\begin{align}
y &= - \frac{x}{2} - 1 \\
y &= - \frac{1}{2} - 1 \\
y &= - 1\frac{1}{2}
\end{align}\]
So, the second missing value is \(- 1\frac{1}{2}\).
All the pairs \((x; y)\) of corresponding \(x\) and \(y\) values are called the solutions of the given
equation. This is because when one value is substituted into the equation, it holds true for the second
value in the same pair.
Some formulas have more than two variables. When there are three variables, we need to find a
“triplet” that satisfies the relationship.
Consider this equation:
\[p = \frac{3m}{4} - \frac{n}{4} + 9\]
Solutions to this equation are the ordered triplets: \((m;n;p)\).
Use the equation to determine the final value in the following ordered triplet so that it solves the
equation: \(( - 8;12;p)\).
The equation has three variables in it. So, you must work out the values of \(m\) and \(n\) which you
should use to get the value of \(p\) in the ordered triplet.
The question states that “solutions to this equation are ordered triplets: \((m;n;p)\)”. This
shows you how the triplets are organised: the variable \(m\) comes first, followed by \(n\). Therefore, in
the triplet \(( - 8;12;p)\) the \(−8\) must be the value of \(m\) and \(12\) must be the value of
\(n\).
The input values from the question are \(m = - 8\) and \(n = 12\).
Evaluate the equation to get the answer for \(p\).
Once you have the input values, just substitute them into the equation and work out the output value,
\(p\).
\[\begin{align}
p &= \frac{3m}{4} - \frac{n}{4} + 9 \\
p &= \frac{3( - 8)}{4} - \frac{12}{4} + 9 \\
&= \frac{- 24}{4} - \frac{12}{4} + 9 \\
&= - 6 - 3 + 9 \\
&= - 9 + 9 \\
&= 0
\end{align}\]
So, the answer is \(p = 0\).
The ordered triplet we were looking for is \(( - 8;12;0)\).
Using relationships between variables
to solve real-world problems
Functions and relationships between variables help us describe and solve different real-world problems. For
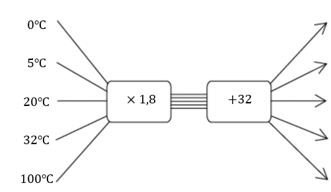
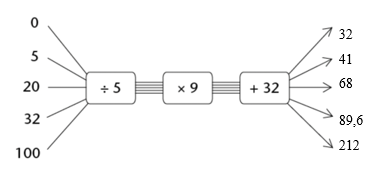
example, the rule for converting temperature given in degrees Celsius to degrees Fahrenheit is given as:
“Multiply the degrees Celsius by \(\text{1,8}\) and then add \(32\).”
We can use this rule to convert between different temperature units.
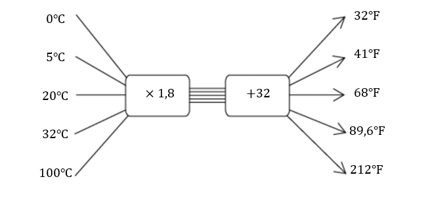
-
\(0^{\circ}\text{C} \ \mathbf{\times \ \text{1,8} + 32} = 32^{\circ}\text{F}\)
-
\(5^{\circ}\text{C} \ \mathbf{\times \ \text{1,8} + 32} = 41^{\circ}\text{F}\)
-
\(20^{\circ}\text{C} \ \mathbf{\times \ \text{1,8} + 32} = 68^{\circ}\text{F}\)
-
\(32^{\circ}\text{C} \ \mathbf{\times \ \text{1,8} + 32} = \text{89,6}^{\circ}\text{F}\)
-
\(100^{\circ}\text{C} \ \mathbf{\times \ \text{1,8} + 32} = 212^{\circ}\text{F}\)
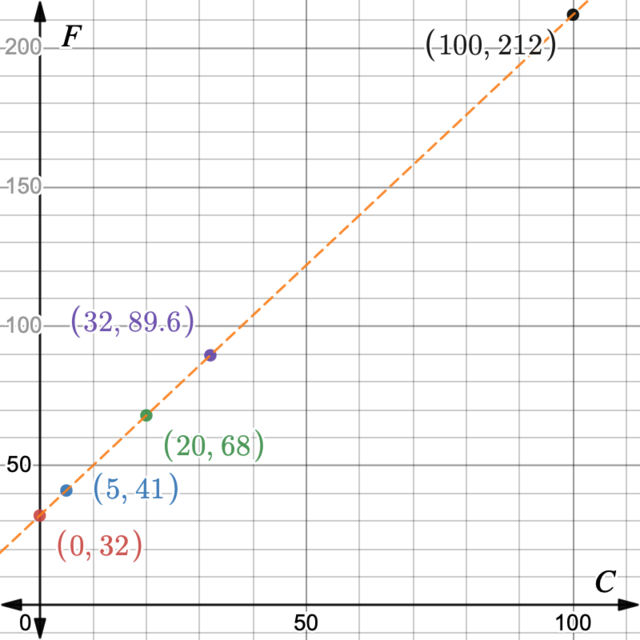
We can complete a table of values for this relationship.
| Temperature in degrees Celsius, \(^{\circ}\text{C}\) |
\(0\) |
\(5\) |
\(20\) |
\(32\) |
\(100\) |
| Temperature in degrees Fahrenheit, \(^{\circ}\text{F}\) |
\(32\) |
\(41\) |
\(68\) |
\(\text{89,6}\) |
\(212\) |
We can then complete a flow diagram to represent this information.
We can also show this relationship as a graph, where the Celsius values are shown on the \(x\)-axis and the
Fahrenheit values are shown on the \(y\)-axis. Plot the points and join them using a line.
This sometimes makes it easier to estimate the values without calculating them. For example, looking at the
graph we can see that \(50^{\circ}\text{C}\) must be approximately equal to \(122^{\circ}\text{F}\).
Check this by calculating:
\[\begin{align}
50^{\circ}\text{C} \times \text{1,8} + 32 &= 90 + 32 \\
&= 122^{\circ}\text{F}
\end{align}\]
The formula for temperature conversion can be written like this:
\(^{\circ}\text{F}=\) \(^{\circ}\text{C} \times \text{1,8} + 32\)
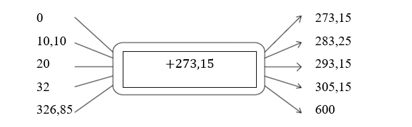
Complete the table of values to convert the temperature readings between degrees Celsius to temperature
units called kelvins. Show this relationship using a flow diagram and a graph.
| Temperature in degrees Celsius, \(^{\circ}\text{C}\) |
\(0\) |
|
\(20\) |
\(32\) |
|
| Temperature in kelvins, K |
|
\(\text{283,25}\) |
|
|
\(600\) |
Here’s the formula to convert kelvins to degrees Celsius:
\[^{\circ}\text{C} = K - \text{273,15}\]
where \(^{\circ}\text{C}\) is the unit temperature in degrees Celsius, and \(K\) is the unit temperature in
kelvins.
The formula to convert degrees Celsius to kelvins is the opposite:
\(K=\) \(^{\circ}\text{C} + \text{273,15}\)
Complete the missing
measurements to find the temperature in degrees Celsius.
Use the formula \(^{\circ}\text{C} = K - \text{273,15}\).
| Temperature in degrees Celsius, \(^{\circ}\text{C}\) |
\(0\) |
\(\text{10,10}\) |
\(20\) |
\(32\) |
\(\text{326,85}\) |
| Temperature in kelvins, K |
|
\(\text{283,25}\) |
|
|
\(600\) |
\[\begin{align}
^{\circ}\text{C} &= \text{283,25} - \text{273,15} \\
&= \text{10,10}
\end{align}\]
\[\begin{align}
^{\circ}\text{C} &= 600 - \text{273,15} \\
&= \text{326,85}
\end{align}\]
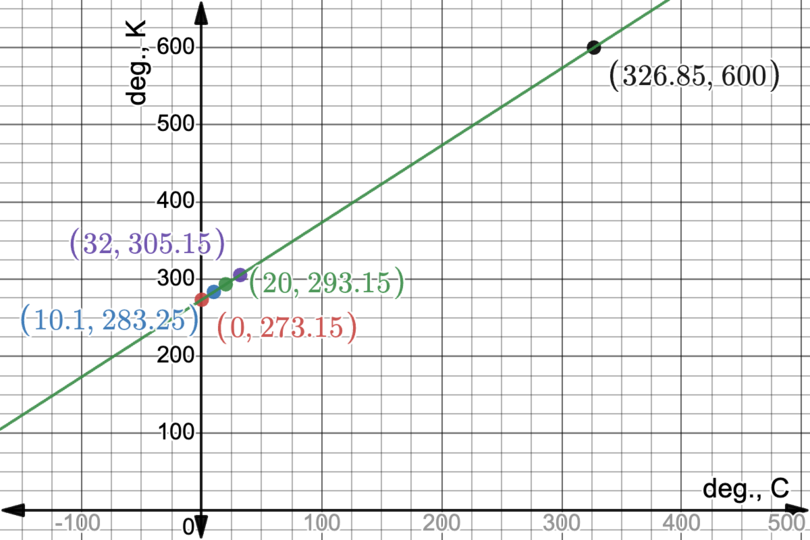
Complete the missing measurements
to find the temperature in Kelvin.
Use the formula \(K = ^{\circ}\text{C} + \text{273,15}\).
| Temperature in degrees Celsius, \(^{\circ}\text{C}\) |
\(0\) |
\(\text{10,10}\) |
\(20\) |
\(32\) |
\(\text{326,85}\) |
| Temperature in kelvins, K |
\(\text{273,15}\) |
\(\text{283,25}\) |
\(\text{293,15}\) |
\(\text{305,15}\) |
\(\text{600}\) |
\[\begin{align}
K &= 0 + \text{273,15} \\
&= \text{273,15}
\end{align}\]
\[\begin{align}
K &= 20 + \text{273,15} \\
&= \text{293,15}
\end{align}\]
\[\begin{align}
K &= 32 + \text{273,15} \\
&= \text{305,15}
\end{align}\]
Illustrate these temperature readings on
the flow diagram.
Plot the points to show the conversion graph.
Exercise 21.1
- The output values will be the same as in the given example, because \(( \div 5 \times 9)\) is the
same as \(( \times 9 \div 5)\)
- The output values will be the same as in the given example, because \(( \div 5 \times 9)\) is the
same as \(\left( \times \frac{9}{5} \right) = ( \times \text{1,8})\).
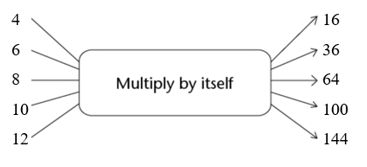
The rule for calculating the area of a square is: “Multiply the length of a side of the square by
itself”.
-
Complete the table below.
| Length of side |
\(4\) |
\(6\) |
|
\(10\) |
|
| Area of square |
|
|
\(64\) |
|
\(144\) |
-
Complete a flow diagram to represent the information in the table.

-
| Length of side |
\(4\) |
\(6\) |
\(8\) |
\(10\) |
\(12\) |
| Area of square |
\(16\) |
\(36\) |
\(64\) |
\(100\) |
\(144\) |
The pattern below shows stacks of building blocks. The number of blocks in each stack is dependent on the
number of the stack.
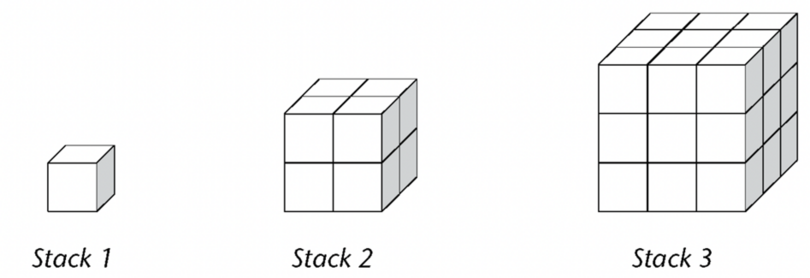
- Complete the table below to represent the relationship between the number of blocks and the number of
the stack.
| Stack number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
| Number of blocks |
\(1\) |
\(8\) |
|
|
|
|
|
|
- Describe in words how the output values can be calculated.
- Write a formula to match the description in b).
-
| Stack number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
| Number of blocks |
\(1\) |
\(8\) |
\(27\) |
\(64\) |
\(125\) |
\(216\) |
\(343\) |
\(512\) |
- “output = input cubed”
-
\[y = x^{3}\]