21.4 Finding a formula from a description
Many problems are formulated in words, and it is often easier to describe the situation than to actually find a solution. The first step in finding a solution to a problem is to try to identify a pattern, then summarise all the known numerical data, and then find a formula that fits the pattern.
Worked Example 21.6: Working with measurements and patterns
Hannelie is conducting an experiment in which the temperature is measured carefully. The temperature was \(97^{\circ}\text{C}\) at the end of the first minute, and then it falls by \(4^{\circ}\text{C}\) every minute after that.
Determine a formula to calculate the temperature (\(T\)) after \(m\) minutes.
Write out the first few terms of the pattern.
We know that the temperature was \(97^{\circ}\text{C}\) at the end of the first minute, and then it falls by \(4^{\circ}\text{C}\) every minute after that. We can represent the first few terms of the pattern in a table:
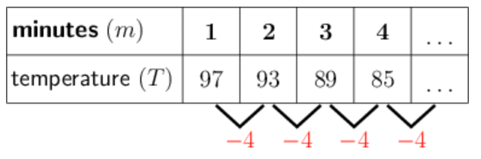
The pattern has a constant difference of \(−4\), so it is a linear pattern.
Determine the formula.
Linear patterns always have a formula that includes the term number multiplied by the constant difference, as well as a constant term.
Therefore, we know that this pattern has the formula \(T = - 4m + \square\). We still need to determine the value of the unknown constant term.
Determine the value of the unknown constant term.
To determine the value of the constant term, we will look at the first term.
We know that the value of the first term is \(97\) (the temperature was \(97^{\circ}\text{C}\) at the end of the first minute).
So, we have:
\[\begin{align} 97 &= - 4 \times 1 + \square \\ 97 &= - 4 + \square \\ \therefore \square &= 101 \end{align}\]Write the final formula.
Therefore, the formula is \(T = - 4m + 101\).
Worked Example 21.7: Working with measurements and patterns
For the same experiment, after how many minutes will the temperature be equal to \(−43^{\circ}\text{C}\)?
Remember that the temperature was \(97^{\circ}\text{C}\) at the end of the first minute, and that it falls by \(4^{\circ}\text{C}\) every minute after that.
To answer the question, use the formula that we found in Worked Example 21.6.
We determined that the formula for the temperature after \(m\) minutes is \(T = - 4m + 101\). We will substitute in \(−43\) for the temperature and solve for \(m\).
Substitute the given value into the formula.
\[\begin{align} T &= - 43 \\ - 43 &= - 4(m) + 101 \end{align}\]Solve for the unknown.
\[\begin{align} - 43 &= - 4m + 101 \\ - 4m + 101 &= - 43 \\ - 4m &= - 43 - 101 \\ - 4m &= - 144 \\ m &= \frac{- 144}{- 4} = 36 \end{align}\]Therefore, the temperature will be equal to \(−43^{\circ}\text{C}\) after \(36\) minutes.
