11.2 Classifying triangles
Properties of triangles
A triangle is a polygon with three straight sides and three interior angles.
- triangle
- a three-sided shape with three straight sides and three interior angles.
- polygon
- a two-dimensional shape with at least three straight sides

The sum of the interior angles of a triangle is equal to \(180^{\circ}\).
In a previous investigation, we cut a triangle into three pieces and arranged the three angles on a straight
line to show that their sum is equal to \(180^{\circ}\).
In \(\triangle PQR\), \(\hat{P} + \hat{Q} + \hat{R} = 180^{\circ}\) (\(\angle\) sum in \(\triangle\))
Some important properties of triangles:
- The longest side of a triangle lies opposite the biggest angle of the triangle.
- The shortest side of a triangle lies opposite the smallest angle of the triangle.
- The sum of the lengths of the two shorter sides of the triangle is greater than the length of the longest
side of the triangle.
Classifying triangles according to their sides
A scalene triangle has no equal sides. All sides are different lengths and all angles are
different sizes.
- scalene triangle
- a triangle that has no equal sides and no equal angles
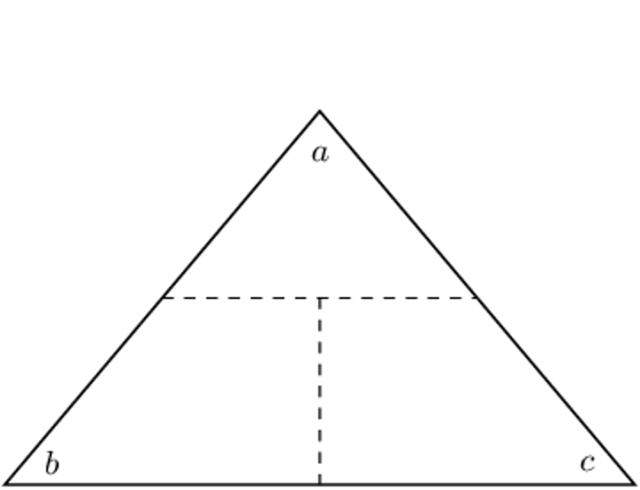
The sides of a triangle can be named according to the vertices of the triangle, for example \(AB\), \(BC\) and
\(CA\). We can also name each side of a triangle using the lower case letter for the vertex that lies opposite
each side. The diagram shows an example of this labelling convention: side \(a\) lies opposite \(\hat{A}\), side
\(b\) lies opposite \(\hat{B}\) and side \(c\) lies opposite \(\hat{C}\).

An isosceles triangle has two equal sides. The two angles opposite the equal sides are also
equal. In \(\triangle PQR\), \(PR = QR\) and \(\hat{P} = \hat{Q}\).
- isosceles triangle
- a triangle with two equal sides

An equilateral triangle has three equal sides. All three sides are the same length and all
three interior angles are equal to \(60^{\circ}\).
- equilateral triangle
- a triangle with has three equal sides

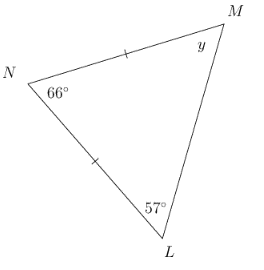
Worked Example 11.1: Finding the missing
angle of a triangle
In \(\triangle LMN\), \(LN = MN\), \(\hat{N} = 66^{\circ}\) and \(\hat{L} = 57^{\circ}\). Find the value of
\(y\).
We know that \(\triangle LMN\) has two equal sides, \(LN = MN\). This means \(\triangle LMN\) is an
isosceles triangle and therefore the angles opposite the equal sides are also equal, \(\hat{L} = \hat{M}\).
Find the value of \(y\).
\[\begin{align}
\hat{L} &= 57^{\circ} (\text{given}) \\
\therefore \hat{M} &= y \\
&= 57^{\circ} (\angle \text{ opp. equal sides})
\end{align}\]
Check answer using sum of angles in triangle.
We can use the sum of angles in a triangle to make sure that the answer is correct:
\[\begin{align}
\hat{L} + \hat{M}+ \hat{N} &= 180^{\circ} (\angle \text{ sum of } \triangle) \\
66^{\circ} + 57^{\circ} + 57^{\circ} &= 180^{\circ} \\
180^{\circ} &= 180^{\circ}
\end{align}\]
The calculation is correct.
Classifying triangles according to their angles
We can also classify triangles according to their interior angles.
An acute-angled triangle has interior angles that are all smaller than \(90^{\circ}\).

A right-angled triangle has one interior angle equal to \(90^{\circ}\). The side opposite the right
angle is called the hypotenuse and it is the longest side of the triangle. In the diagram
below, the first triangle is a right-angled isosceles triangle.
- hypotenuse
- the longest side in a right-angled triangle, which is also opposite the right angle itself

An obtuse-angled triangle has one interior angle greater than \(90^{\circ}\) but less than
\(180^{\circ}\). In the diagram below, the last triangle is an obtuse-angled isosceles triangle.

Use the given information to classify the triangle as accurately as possible.

The diagram shows that two angles of the triangle are equal. Therefore, we know that the two sides opposite
the equal angles are equal in length and the triangle is an isosceles triangle.
Using the sum of angles in a triangle we can determine the size of the third angle in the triangle.
\[\begin{align}
\text{Third angle} &= 180^{\circ} − 48^{\circ} − 48^{\circ} \\
&= 84^{\circ}
\end{align}\]
The third angle in the triangle is an acute angle.
Write the final answer
This is an acute-angled isosceles triangle.
Use the given information to classify the triangle as accurately as possible.

The size of each interior angle of the triangle is given and they are all different sizes. One interior
angle is an obtuse angle. No information about the sides of the triangle is given.
Write the final answer.
This is an obtuse-angled scalene triangle.
Use the given information to classify the triangle as accurately as possible.

The diagram shows that one interior angle is a right angle and two sides of the triangle are equal.
Write the final answer.
This is a right-angled isosceles triangle.
Exercise 11.1
Match each type of triangle with the correct description.
| Type of triangle |
Description |
| 1. Isosceles triangle |
A. All the sides of a triangle are equal. |
| 2. Obtuse-angled triangle |
B. One interior angle is equal to \(90^{\circ}\) |
| 3. Scalene triangle |
C. None of the sides of a triangle are equal. |
| 4. Right-angled triangle |
D. All interior angle are less than \(90^{\circ}\). |
| 5. Equilateral triangle |
E. One interior angle is greater to \(90^{\circ}\) and less than \(180^{\circ}\). |
| 6. Acute-angled triangle |
F. Two sides of a triangle are equal. |
Name each type of triangle.
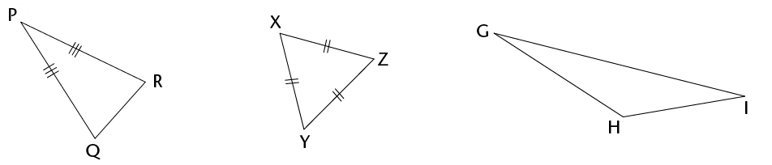
- \(\triangle PQR\) is an isosceles triangle.
- \(\triangle XYZ\) is an equilateral triangle.
- \(\triangle GHI\) is a scalene triangle.
For each triangle below, the marked angles are equal. Classify the triangles according to angle and side
properties.
- \(\triangle JKL\) is a … triangle because …
- \(\triangle MNO\) is a … triangle because …
- \(\triangle PQR\) is a … triangle because …
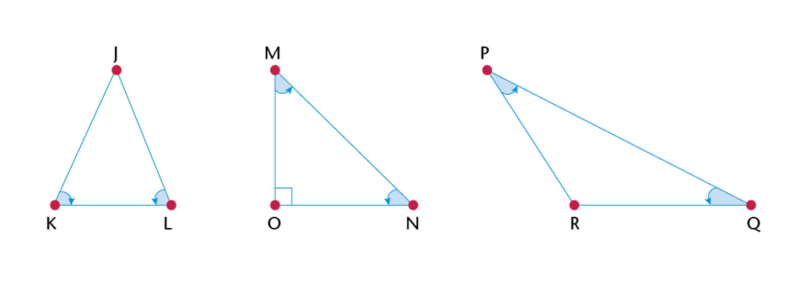
- \(\triangle JKL\) is an isosceles triangle because two angles are equal.
- \(\triangle MNO\) is a right-angled isosceles triangle because one angle is a right angle and the
other two angles are equal.
- \(\triangle PQR\) is an obtuse-angled isosceles triangle because one angle is greater than
\(90^{\circ}\) and the other two angles are equal.
For each statement below, decide if it is true for any of the three triangles in question 1 (\(\triangle
JKL\), \(\triangle MNO\) and \(\triangle PQR\)). If it is true for all triangles, then write ‘All
triangles’. If it is not true for any of the triangles, write ‘None’.
- The sum of the interior angles is \(180^{\circ}\).
- Two sides of the triangle are equal.
- One angle of the triangle is obtuse.
- The sum of the two shorter sides of the triangle is bigger than the length of the longest side.
- Two angles of the triangle are equal.
- All three angles of the triangle are equal to \(60^{\circ}\).
- The longest side of the triangle is opposite the biggest angle.
- All three sides of the triangle are equal.
- All triangles
- All triangles
-
\(\triangle PQR\)
- All triangles
- All triangles
- None
- All triangles
- None
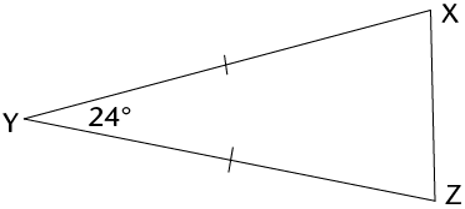
Worked Example 11.5: Finding the
size of unknown angles in a triangle
Find the size of \(\hat{X}\) and \(\hat{Z}\).
The diagram shows that \(XY = ZY\), so \(\triangle XYZ\) is an isosceles triangle. So we know that
\(\hat{X}\) and \(\hat{Z}\) are equal (angles opposite equal sides).
\[\therefore \hat{X} = \hat{Z}\]
Calculate the size of the unknown angles.
We know that \(\hat{Y} = 24^{\circ}\) and \(\hat{X} = \hat{Z}\), so we can use sum of angles in a triangle
to calculate the size of \(\hat{X}\) and \(\hat{Z}\).
\[\text{Let } \hat{X} = \hat{Z} = p\]
\[\begin{align}
\hat{X} + \hat{Y} + \hat{Z} &= 180^{\circ} \\
p + 24^{\circ} + p &= 180^{\circ} \\
2p &= 156^{\circ} \\
p &= 78^{\circ}
\end{align}\]
Write the final answer.
\[\hat{X} = \hat{Z} = 78^{\circ}\]
Exterior angles of a triangle
So far we have considered the interior angles of triangles and the special relationships between angles and
sides of a triangle. In this next section, we will investigate the relationship between the exterior angles of a
triangle and the interior angles.
If the side of a triangle is extended, the angle formed between the side of the triangle and the extended side
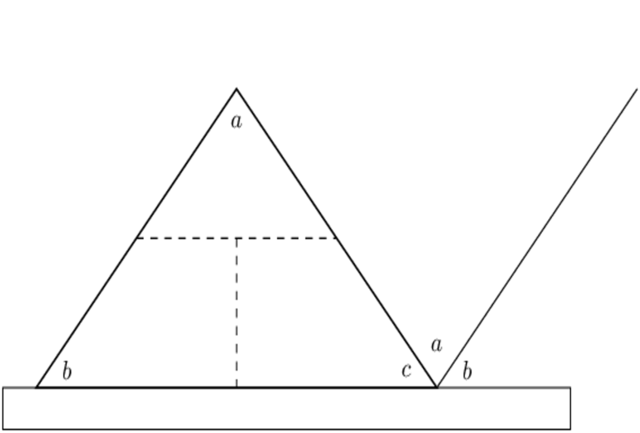
is an exterior angle of the triangle. In the diagram below, \(p\), \(q\) and \(r\) are examples of exterior
angles of the triangle.

Exterior angles of a triangle
For this investigation, you will need two pieces of paper, a pencil, a ruler and a pair of scissors.
- On the piece of paper, draw a triangle of any size and shape. On the other piece of paper, make a copy of
the triangle.
- Use the pair of scissors to cut out both triangles.
- Label the interior angles of both triangles \(a\), \(b\) and \(c\).
- Draw dotted lines on one triangle as shown in the diagram above. Cut along the lines.
- Draw a straight line on a piece of paper and place the second triangle on the line. Arrange the cut out
pieces of the first triangle (vertex \(a\) and vertex \(b\)) as shown in the figure below.
- What do you notice? Write down your observations in a sentence.
The exterior angle of a triangle is equal to the sum of the two interior opposite angles.

\[\begin{align}
\hat{A} + \hat{B} + \hat{C}_{1} &= 180^{\circ} (\angle \text{ sum in } \triangle) \\
\hat{C}_{1} + \hat{C}_{2} &= 180^{\circ} (\angle \text{ on str. line})
\end{align}\]
Since both expressions equal \(180^{\circ}\), we can make them equal to each other:
\[\hat{A} + \hat{B} + \hat{C}_{1} = \hat{C}_{1} + \hat{C}_{2}\]
We can simplify the equation:
\[\hat{A} + \hat{B} = \hat{C}_{2}\]
This tells us that the exterior angle of a triangle (\(\hat{C}_{2}\)) is equal to the sum of the two interior
opposite angles (\(\hat{A} + \hat{B}\)):
\[\hat{C}_{2} = \hat{A} + \hat{B } (\text{ext. } \angle \text{ of } \triangle)\]
Worked Example 11.6: Calculating angles of a
triangle
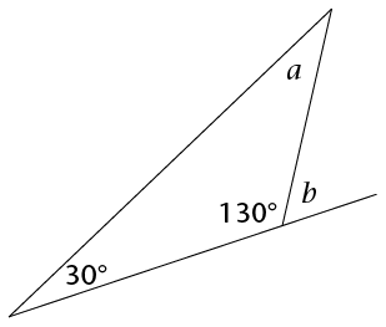
Determine the values of \(a\) and \(b\).
Calculate \(a\) using the angle sum of a triangle.
Two of the interior angles of the triangle are given, so we can use sum of the angles in a triangle to
calculate the size of \(a\).
\[\begin{align}
a + 30^{\circ} + 130^{\circ} &= 180^{\circ} \\
a &= 180^{\circ} − 160^{\circ} \\
a &= 20^{\circ}
\end{align}\]
Calculate exterior angle \(b\).
We know that the exterior angle of a triangle is equal to the sum of the two interior opposite angles:
\[\begin{align}
b &= 30^{\circ} + a \\
&= 30^{\circ} + 20^{\circ} \\
&= 50^{\circ}
\end{align}\]
Check the answer.
Notice that \(b\) and \(130^{\circ}\) angle are on a straight line. The sum of angles on a straight line is
\(180^{\circ}\). We can use this to check the value of \(b\):
\[\begin{align}
b + 130^{\circ} &= 180^{\circ} \\
b &= 180^{\circ} − 130^{\circ} \\
&= 50^{\circ}
\end{align}\]