25.6 Building 3D models
Nets of cubes
In Chapter 17 on surface area and volume, you learned about the nets of 3D shapes. A net is what a 3D shape, for example a box, looks like if it is opened out flat: it is a flat diagram that can be folded to form a three-dimensional shape
A cube is a solid with six identical square faces at right angles to each other. So the net of a cube consists of six congruent squares.
Nets of cubes
For this investigation, you will need a pencil, a ruler, a compass, a protractor, a pair of scissors and glue. You will also need something pointy to score the edges. Scoring a line means making a crease-line on the paper which makes it easier to fold. You can use the edge of a ruler, the end of a paper clip or the point of your compass. Press lightly when you score each edge so that you do not tear the piece of paper.
- Use a compass and a protractor to construct six squares with length \(s = 7 \text{ cm}\), touching each
other as shown in the diagram.
- To build a 3D model of a cube, we need to be able to join the faces to make an edge. We can do this by
creating tabs on some of the sides of the squares. To create a tab, draw a small rectangle on each side of
the square. The width of the rectangle can be between \(5 \text{ mm}\) and \(10 \text{ mm}\). Cut the corner
off the ends of each rectangle – this will make the tabs easier to fold and stick.
- Use scissors to cut out the net and score all the lines that need to be folded. (These are shown in red in
the diagram.)
- Fold the lines and use glue to stick the tabs together. Remember to hold the two tabs together for a few seconds to help them stick.
- This net configuration was one of many possible configurations for a cube. A different configuration for
the net for a cube is shown below. How many others can you find?
Nets of prisms
Rectangular prisms
A rectangular prism (also called a cuboid) is a solid with six rectangular faces at right angles to each other.
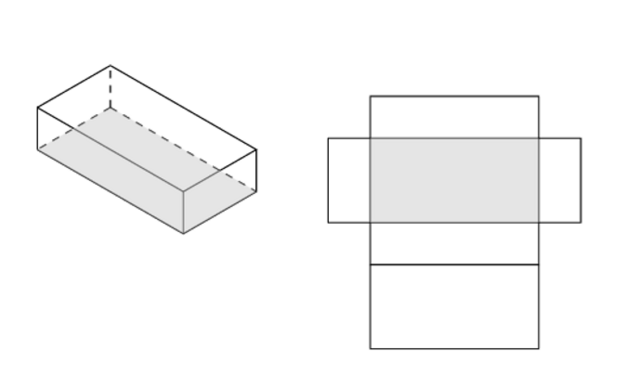
Nets of rectangular prisms
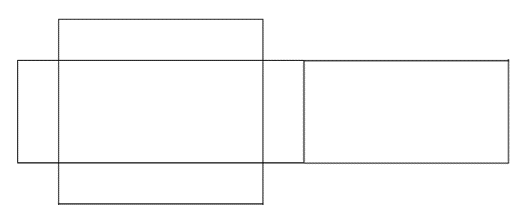
For this investigation, you will need a pencil, a ruler, a compass, a protractor, a pair of scissors and glue. You will also need something pointy to score the edges. You will construct a 3D model of the rectangular prism shown below.
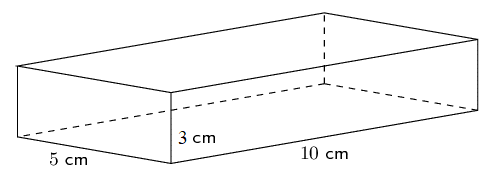
- Use a ruler and a protractor to construct the net of the cuboid as shown in the diagram.
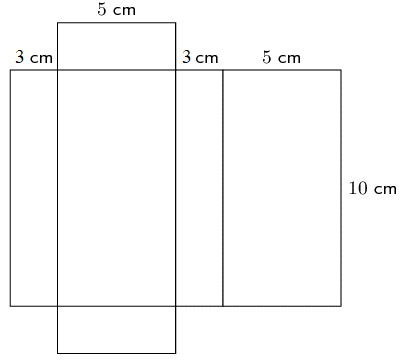
- Add tabs to the net and cut out the shape. Remember to score lines that need to be folded.
- Fold and glue the tabs together.
- Count the number of faces, edges and vertices of your 3D model. Do these values satisfy Euler’s formula?
- Look at the diagram below. Would this net produce the same prism as the rectangular prism that you have
constructed? (You can assume the dimensions are the same.)
Triangular prisms
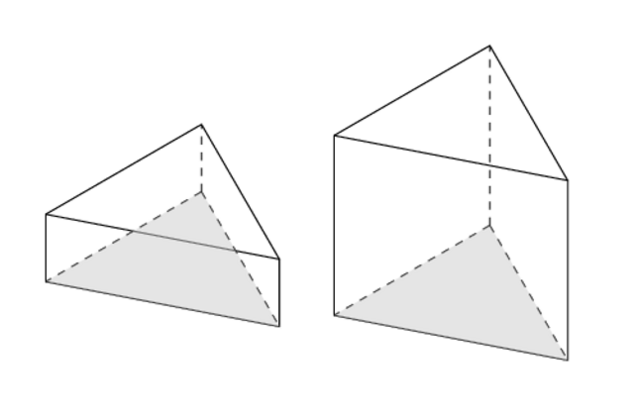
A triangular prism has two identical triangular bases and three rectangular sides joined at right angles to the bases.
Nets of triangular prisms
For this activity, you will need a pencil, a ruler, a compass, a protractor, a pair of scissors and glue. You will also need something pointy to score the edges.
You will construct a 3D model of the triangular prism shown below. The base is an equilateral triangle with sides \(l = 7 \text{ cm}\) and the height of the prism is \(h = 6 \text{ cm}\).
- Make a sketch of the net of the triangular prism. Mentally fold the net to make sure that your net configuration will form the prism. Remember there can be different configurations of nets for the same object.
- What is the size of each interior angle of an equilateral triangle?
- Use a ruler and a protractor to construct the triangular base.
- Complete the rest of the net of the triangular prism and add tabs.
- Cut out the net and score lines that will be folded.
- Fold and glue the tabs together to form the prism.
- Count the number of faces, edges and vertices of your model. Do these values satisfy Euler’s formula?
Nets of pyramids
A pyramid is an object that has a polygon as its base and triangular sides that converge (meet each other) at one single point called the apex. The sides are not perpendicular to the base.
- pyramid
- an object that has a polygon as its base and triangular sides that converge at an apex
- apex
- the highest point of an object; it is usually the vertex opposite the base
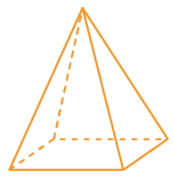
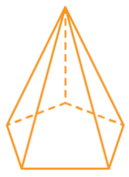
A pyramid can have any polygon as its base. The diagrams below show a square-based pyramid, a pentagon-based pyramid and a hexagon-based pyramid. Notice that these are examples of regular polygon bases.
| Square-based pyramid | Pentagon-based pyramid | Hexagon-based pyramid |
|---|---|---|
 |
 |
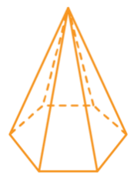 |
Nets of square-based pyramids
For this activity, you will need a pencil, a ruler, a compass, a protractor, a pair of scissors and glue. You will also need something pointy to score the edges.
You will construct a 3D model of the square-based pyramid shown below. The sides of the square are \(4 \text{ cm}\) and the height of each triangle is \(\text{4,5} \text{ cm}\).
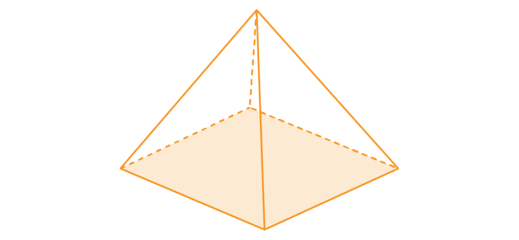
- Sketch the net of the square-based pyramid. Mentally fold the net to make sure that your net configuration will form the pyramid.
- Use a ruler and a protractor to construct the square base with the sides of the square equal to \(4 \text{ cm}\).
- Find the midpoint of each side of the square and measure a perpendicular height of \(\text{4,5} \text{ cm}\).
- Join each point to the two corners of the square that lie on either side of the perpendicular height. Four congruent triangles are formed.
- Add tabs to the net and cut out the shape. Remember to score lines that need to be folded.
- Fold and glue the tabs together.
- Count the number of faces, edges and vertices of your 3D model. Do these values satisfy Euler’s formula?
Nets of the Platonic solids
The net of a tetrahedron is made up of four congruent equilateral triangles.
The net of a hexahedron is made up of six congruent squares.
The net of an octahedron is made up of eight congruent equilateral triangles.
The net of a dodecahedron is made up of twelve congruent regular pentagons.
The net of an icosahedron is made up of twenty congruent equilateral triangles.
Three of the Platonic solids have triangular faces (tetrahedron, octahedron and icosahedron), one has square faces (hexahedron), and one has pentagonal faces (dodecahedron).
Nets of the Platonic solids
-
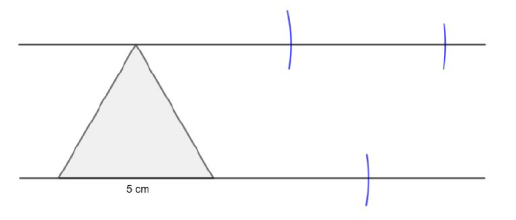
Construct a net for a tetrahedron with sides of \(5 \text{ cm}\). You can make all the faces different colours. Can you think of any techniques that will make constructing the net easier?
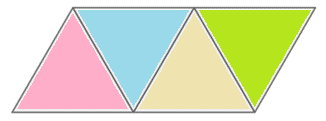
Construct an equilateral triangle and then draw parallel lines. Use a compass to mark off distances of \(5 \text{ cm}\).
- Add tabs to the net and cut out the shape.
- Score the lines that need to be folded.
- Glue the tabs to form the tetrahedron.
- How many faces meet at a vertex?
-
Construct a net for an octahedron with sides of \(5 \text{ cm}\). You can make all the faces different colours.
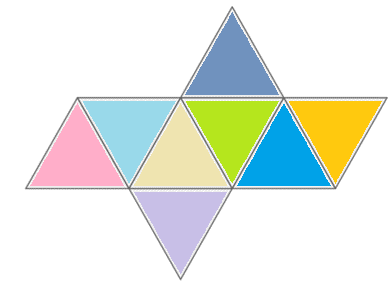
- Add tabs to the net and cut out the shape.
- Score the lines that need to be folded.
- Glue the tabs to form the octahedron.
- How many faces meet at a vertex?
-
Construct a net for an icosahedron with sides of \(5 \text{ cm}\). You will need a full A4 piece of paper for this net.
You can make the rows of triangles different colours. Choose your own pattern.
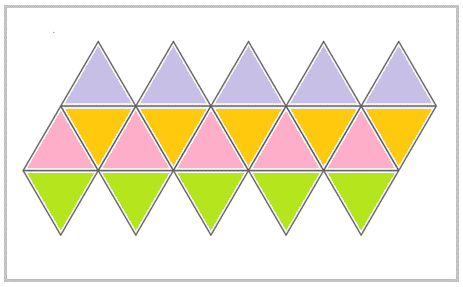
- Cut out the shape and score the lines that need to be folded.
- Fold the net to form an icosahedron.
- How many faces meet at a vertex?
-
Construct a net for a dodecahedron with sides of \(4 \text{ cm}\). You will need a full A4 piece of paper for this net.
You can make the pentagons different colours. Choose your own pattern.
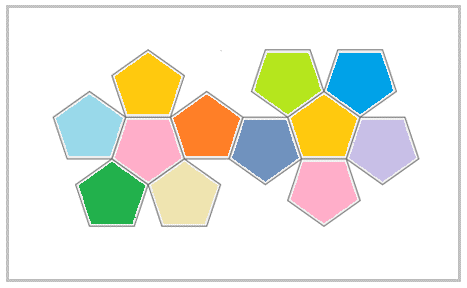
- Cut out the shape and score the lines that need to be folded.
- Fold the net to form a dodecahedron.
- How many faces meet at a vertex?
