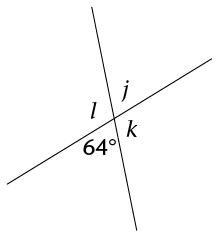
Calculate the size of \(j\), \(k\) and \(l\).
|
Previous
Angles on a straight line
|
Next
Angles formed by lines intersected by a transversal
|
In the diagram below, two straight lines intersect at a point, forming the four angles \(\hat{a}, \hat{b}, \hat{c} , \text {and } \hat{d}\).
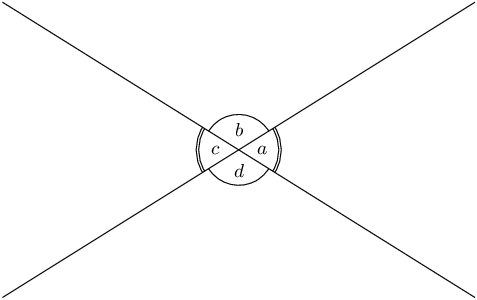
Vertically opposite angles (vert opp \(\angle\)s) are the angles opposite each other when two lines intersect.
Vertically opposite angles are always equal. In the diagram above, \(\hat{a}=\hat{c}\) and \(\hat{b}=\hat{d}\).
All the angles around one point form a revolution. One revolution is equal to \(360^{\circ}\).
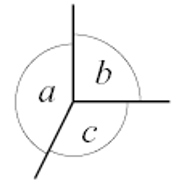
In the diagram below, the three angles \(\hat{a}\), \(\hat{ b}\), and \(\hat{c}\) form a revolution.
\(\hat{a}+\hat{b}+\hat{c}= 360^{\circ}\) (\(\angle\)s around a point)
Calculate the size of \(x\), \(y\) and \(z\).
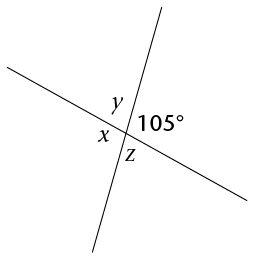
Here we can see that:
\(y\) and \(105^{\circ}\) are angles on the same side of the straight line, so their sum must be \(180^{\circ}\).
We can write out an equation, and then solve for \(m\).
\[\begin{align} m + 20^{\circ} &= 100^{\circ}&& (\text{vert opp }\angle\text{s}) \\ m &= 100^{\circ} - 20^{\circ} \\ &= 80^{\circ} \end{align}\]Calculate the size of \(y\), giving a reason for your answer.

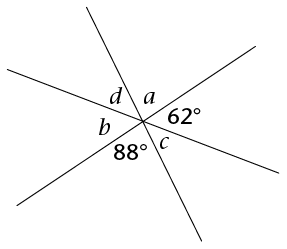
In this diagram, we see that the four marked angles are all angles around the same point. We will use the fact that angles around a point add up to \(360^{\circ}\) to form an equation to help us solve for \(y\).
Calculate the size of \(j\), \(k\) and \(l\).

Calculate the size of \(a\), \(b\), \(c\) and \(d\).
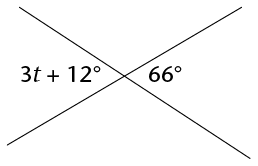
Calculate the size of \(t\).
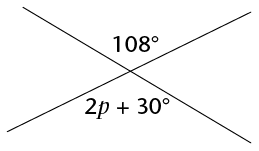
Calculate the size of \(p\).
|
Previous
Angles on a straight line
|
Table of Contents |
Next
Angles formed by lines intersected by a transversal
|