12.6 Solving more geometric problems
When solving geometry problems involving lines, you need to use some facts about quadrilaterals and triangles.
- The sum of the interior angles of a triangle is \(180^\circ\).
- The exterior angle of a triangle is equal to the sum of the interior opposite angles.
- exterior angle of a triangle
- the angle formed outside a triangle when one of its sides is produced
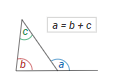
- The interior angles of a quadrilateral add up to \(360^{\circ}\).
\(\hat{P}+\hat{Q}+\hat{R}+\hat{S}= 360^{\circ}\)
- interior angle
- an angle that lies inside a shape
Worked example 12.9: Identifying angles on
parallel lines
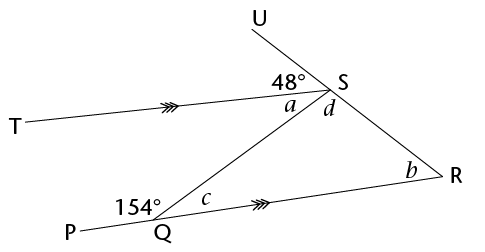
Calculate the size of angles \(a\), \(b\), \(c\) and \(d\).
Examine the parallel lines.
Identify how many transversals there are.
Notice that there are two traversals: \(SQ\) and \(UR\). Now look for the angles that form F or Z pattern
along each transversal.
- Transversal \(UR\): We can see that \(b\) is a corresponding angle to \(48^{\circ}\), making an F
pattern. There are no alternate angles formed by this transversal.
- Transversal \(SQ\): We can see that \(a\) is alternate to \(c\), making a Z pattern. There are no
corresponding angles formed by this transversal.
Look for any
adjacent supplementary angles that can help you find one of the angles.
Angle \(c\) is an adjacent supplementary angle to 154°.
Write out your solution.
\[\begin{align}
b & = 48^{\circ}&&(\text{corresp }\angle\text{s; } TS \parallel PR) \\
c & = 180^{\circ} - 154^{\circ}&&(\angle\text{s on a straight line}) \\
c & = 26^{\circ} \\
a & = 26^{\circ}&&(\text{alt }\angle\text{s; } TS \parallel PR) \\
d & = 180^{\circ}-48^{\circ} - 26^{\circ} &&(\angle\text{s on a straight line}) \\
d & = 106^{\circ}
\end{align}\]
Worked example 12.10: Using angles on parallel lines
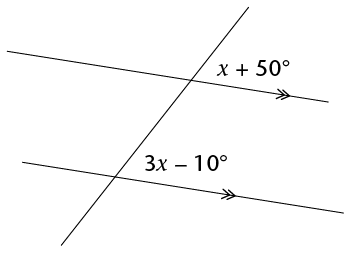
Calculate the size of \(x\).
\[\begin{align}
x+50^{\circ} &= 3x-10^{\circ} &&(\text{corresp }\angle\text{s}) \\
x-3x &= -10^{\circ} -50^{\circ} \\
-2x &= -60^{\circ} \\
x &= 30^{\circ}
\end{align}\]
Worked example 12.11: Using angles on parallel lines
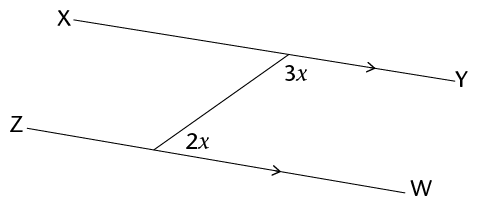
Calculate the size of \(x\).
Notice that there is only one transversal in this diagram. The two given angles make a C pattern.
The two angles form co-interior angles, which add up to \(180^{\circ}\), because the lines are parallel. So we
can write out an equation using this information.
\[\begin{align}
2x+3x &= 180^{\circ} &&(\angle\text{s on a straight line}) \\
5x &= 180^{\circ} \\
x &= 30^{\circ} \\
\end{align}\]
Worked example 12.12: Solving geometric problems involving properties of triangles
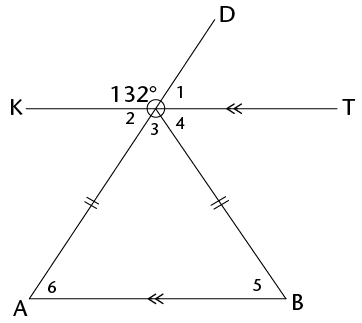
Calculate the sizes of \(\hat{1}\) to \(\hat{6}\).
Examine the diagram
carefully. Look for the parallel lines and all transversals.
Notice that there are two transversals; \(AD\) and \(OB\):
- Looking at \(AD\), notice that \(\hat{2}\) and \(\hat{6}\) are alternate angles and therefore equal. We also
see that \(\hat{1}\) and \(\hat{6}\) are corresponding angles and therefore equal.
- Looking at \(OB\), we notice that \(\hat{4}\) and \(\hat{5}\) are alternate angles.
Look for all the adjacent angles on a straight
line.
You may need to use the fact they are supplementary later in your calculation. How many supplementary
angles can you find?
The supplementary angles are:
\[\begin{align}
132^\circ+\hat{2}&=180^\circ \\
132° + \hat{1}&=180^\circ \\
\hat{2}+\hat{3} + \hat{4}&=180^\circ \\
\hat{1} + \hat{3}+ \hat{4}&=180^\circ
\end{align}\]
Look for vertically opposite angles.
How many can you find? (\(\hat{1}\) is vertically opposite \(\hat{2}\)).
Write out your solution.
\[\begin{align}
\hat{1}&= 180^{\circ} -132^{\circ} &&(\angle\text{s on a straight line}) \\
\hat{1}&= 48^{\circ} \\
\hat{2}&= 48^{\circ} &&(\text{vert opp }\angle\text{s}) \\
\hat{6}&= 48^{\circ} &&(\text{alt }\angle\text{s; KT} \parallel {AB})
\end{align}\]
Hint: Remember that in an isoceles triangle, two sides are the same length.
Because \(\triangle ABO\) is an isoceles triangle:
\[\begin{align}
\hat{5}&= 48^{\circ} &&(\angle\text{s equal opp sides}) \\
\hat{3} &= 180^{\circ}- \hat{5}- \hat{6} &&(\angle\text{s in a }\triangle) \\
\hat{3} &= 180^{\circ}-48^{\circ}-48^{\circ} \\
\hat{3} &= 84^{\circ}
\end{align}\]
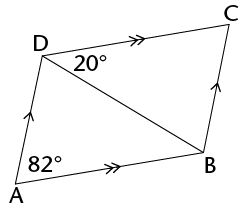
Worked example 12.13: Solving geometric problems involving properties of triangles and quadrilaterals
\(ABCD)\ is a parallelogram. Calculate the sizes of \(A\hat{B}D\), \(A\hat{D}B\), \(\hat{C}\) and
\(C\hat{B}D\).
Both pairs of opposite angles are equal in a parallelogram, therefore we can say that \(\hat{A}=\hat{C}\).
We are given two sets of parallel lines: \(AD \parallel BC\) and \(DC \parallel AB\).
- \(DC \parallel AB\): Looking at transversal \(BD\), we notice that \(20^{\circ}\) and \(\hat{DBA}\) are
alternate angles formed by these parallel lines, and therefore are equal.
- \(AD \parallel BC\): Looking at transversal \(BD\), we notice that \(\hat{ADB}\) and \(\hat{DBC}\) are
alternate angles formed by these parallel lines, and therefore are equal.
Use the properties of triangles to find angles.
We are also given two triangles: \(\triangle{ABD}\) and \(\triangle{DBC}\). We can use the fact that the
sum of \(\angle\)s of a \(\triangle\) = \(180^\circ\) to help find remaining angles.
Write out your solution.
\[\begin{align}
\hat{ABD}&= 20^{\circ} &&(\text{alt }\angle\text{s; AB} \parallel {DC}) \\
\hat{ADB}&= 180^{\circ} -20^{\circ}-82^{\circ} &&(\angle\text{s in a }\triangle) \\
\hat{ADB}&= 78^{\circ} \\
\hat{C} &= 82^{\circ} &&(\text{opp sides of parallelogram}) \\
\hat{CBD}&= 78^{\circ} &&(\text{alt }\angle\text{s; AB} \parallel {DC})
\end{align}\]
Exercise 12.7
\(RSTU\) is a trapezium. Calculate the sizes of \(\hat{T}\) and \(\hat{R}\).
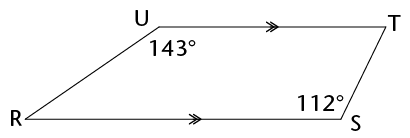
\[\begin{align}
\hat{R} &=180°-143° &&(\text{co-int}\angle\text{s}; UT \parallel RS) \\
\hat{R} &= 37° \\
\hat{T} &=180°-112° &&(\text{co-int}\angle\text{s}; UT \parallel RS) \\
\hat{T} &= 68°
\end{align}\]
\(JKLM\) is a rhombus. Calculate the sizes of of \(J\hat{M}L\), \(\hat{M}_2\) and \(\hat{K}_1\).
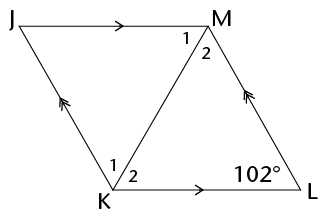
Hint: Remember, \(JKLM\) is a rhombus, therefore all four sides of \(JKLM\) are equal.
\[\begin{align}
\hat{J} &=102° &&(\text{opp }\angle\text{s of rhombus)} \\
\hat{M_2} &= \hat{K_2} &&(\text{opp }\angle\text{s; } \text { opp = sides; ML = KL}) \\
\hat{M_2} + \hat{K_2} +102° &= 180° \\
\hat{M_2} + \hat{K_2} +102° &= 180° - 102° \\
\hat{M_2} + \hat{K_2} +102° &= 78° \\
\hat{M_2} = \hat{K_2} &= 39° \\
\text{Similarly, } \hat{M_1} = \hat{K_1} &= 39° \\
J\hat{M}L &= \hat{M_1} + \hat{M_2} \\
&= 78°
\end{align}\]
In the diagram, \(AB \parallel CD\). Calculate the sizes of \(F\hat{H}G, \hat{F},\hat{C}\) and \(\hat{D}\).
Give reasons for your answers.
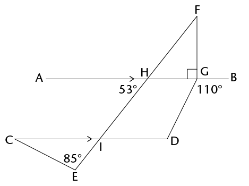
\[\begin{align}
\hat{FHG} &=53° && (\text{vert opp }\angle\text{s}) \\
\hat{F}+ \hat{FHG}+ 90° &=180°&&(\text{sum of }\angle\text{s in } \triangle )\\
\hat{F}+53°+ 90° &=180° \\
\hat{F}&=180° -90°-53° \\
\hat{F}&=37° \\ \\
\hat{CIE} &= 53° &&(\text{corresp }\angle\text{s}; AB \parallel CD) \\
\hat{C}+ \hat{E}+ \hat{CIE} &=180°&&(\text{sum of }\angle\text{s in } \triangle)\\
\hat{C}+85°+53° &=180° \\
\hat{C}&=180° -85°-53° \\
\hat{C}&=42° \\ \\
\hat{AGD} &= 180°-110 &&(\angle\text{s on a str line})\\
\hat{AGD} &= 70° \\
\hat{D} &= 180°-70° &&(\text{co-int }\angle\text{s}; AB \parallel CD) \\
\hat{D} &= 110°
\end{align}\]