23.5 The Cartesian plane
The Cartesian coordinate system consists of two axes. The \(x\)-axis is a horizontal line at \(y = 0\) and the \(y\)-axis is a vertical line at \(x = 0\). The point where the two lines intersect is called the origin. At the origin, \(x = 0\) and \(y = 0\).
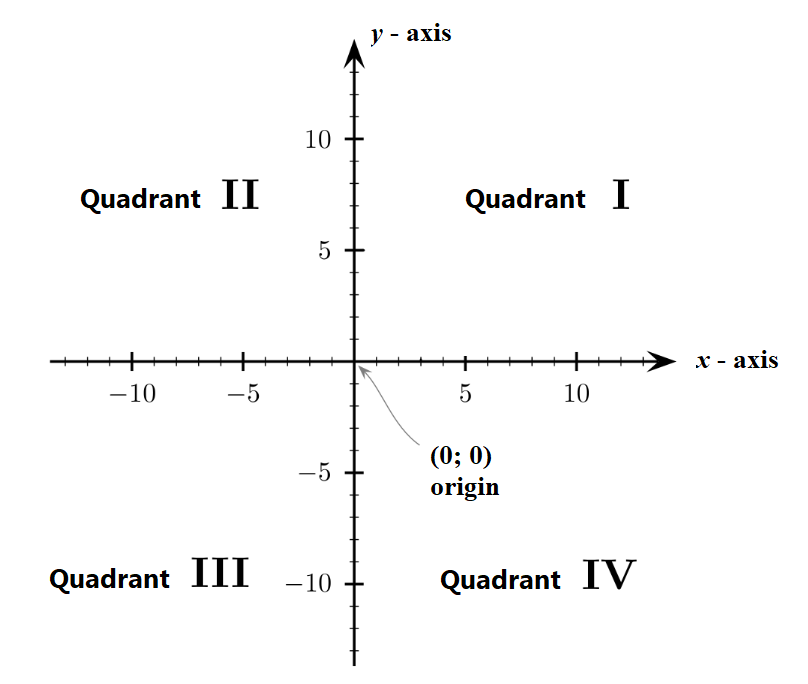
Adapted from Gustavb, Wikimedia, GNU Free Documentation License
The \(x\)-axis and the \(y\)-axis divide the Cartesian plane into four quadrants.
- In the first quadrant (I), the values of the \(x\)-axis are positive and the values of the \(y\)-axis are also positive.
- In the second quadrant (II), the values of the \(x\)-axis are negative and the values of the \(y\)-axis are positive.
- In the third quadrant (III), the values of the \(x\)-axis are negative and the values of the \(y\)-axis are also negative.
- In the fourth quadrant (IV), the values of the \(x\)-axis are positive and the values of the \(y\)-axis are negative.
The position of any point on the Cartesian plane can be represented by a set of coordinates called an ordered pair. An ordered pair consists of an \(x\)-value called the \(x\)-coordinate and a \(y\)-value called the \(y\)-coordinate. The two values are written in brackets and separated by a semicolon.
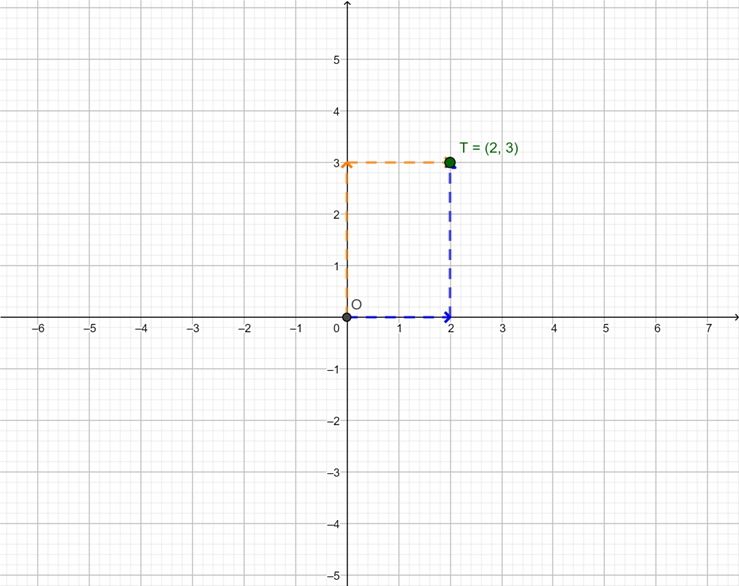
The diagram shows point \(T(2; 3)\) plotted on the Cartesian plane. For point \(T\), the value of the \(x\)-coordinate is 2, and the value of the \(y\)-coordinate is 3. On the \(x\)-axis, point \(T\) is 2 units from the origin in a positive direction (to the right). On the \(y\)-axis, point \(T\) is \(3\) units from the origin in a positive direction (upwards). The position of point \(T\) from the origin can be described as:
- 2 units to the right on the \(x\)-axis and 3 units upwards (blue lines)
or
- 3 units upwards on the \(y\)-axis and 2 units to the right (orange lines).
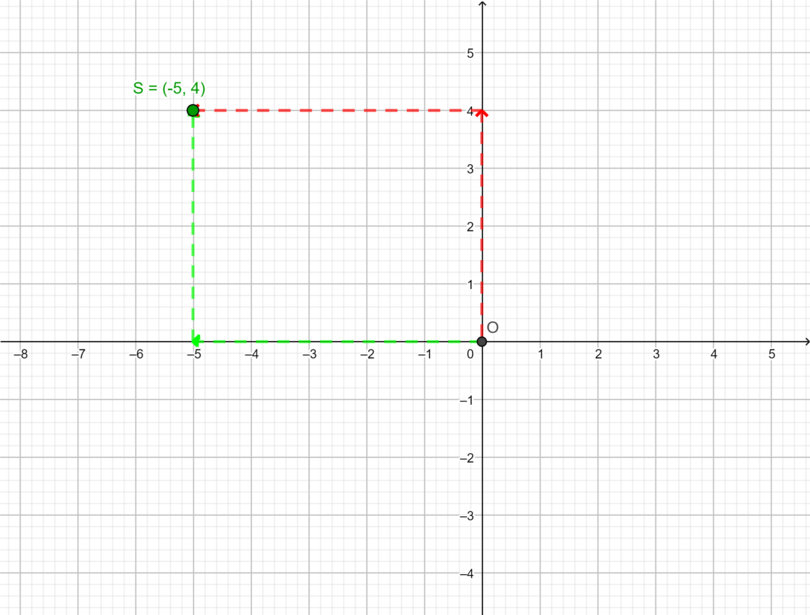
The diagram below shows point \(S(-5; 4)\) plotted on the Cartesian plane. For point \(S(-5; 4)\), the value of the \(x\)-coordinate is \(-5\) and the value of the \(y\)-coordinate is 4. On the \(x\)-axis, point \(S\) is 5 units from the origin in a negative direction (to the left) and on the \(y\)-axis, point \(S\) is 4 units from the origin in a positive direction (upwards). The position of point \(S\) from the origin can be described as:
- \(5\) units to the left on the \(x\)-axis and \(4)\ units upwards (green lines)
or
- \(4\) units upwards on the \(y\)-axis and \(5)\ units to the left (red lines).
Worked example 23.3: Reading the coordinates of points on the Cartesian plane
The graph below shows the Cartesian plane and four points. The points are labelled \(A\), \(B\), \(C\) and \(D\). Which point has the coordinates \((5; 1)\)?
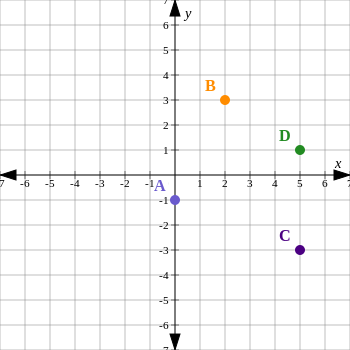
Look at the information in the diagram.
There are four points shown in the diagram, and we must decide which of the points has the coordinates \((5; 1)\). Coordinate pairs always show the \(x\)-coordinate first and the \(y\)-coordinate second. In this case that means that \(x = 5\) and \(y = 1\).
To find the position of the point on the Cartesian plane, we start at the origin. From there, the coordinates tell us the number of units and the direction we must move:
- the \(x\)-coordinate tells us how many units to move on the \(x\)-axis (left or right)
- the \(y\)-coordinate tells us how many units to move on the \(y\)-axis (up or down)
Use the coordinates to find the position of the point.
- Starting with the \(x\)-value: For the coordinates \((5; 1)\), \(x = 5\), from the origin, we need to move \(5\) units to the right (we move to the right on the \(x\)-axis because the coordinate has a positive value).
- For the coordinates \((5; 1)\), \(y = 1\), go 1 unit upwards (we move upwards because the coordinate has a positive value).
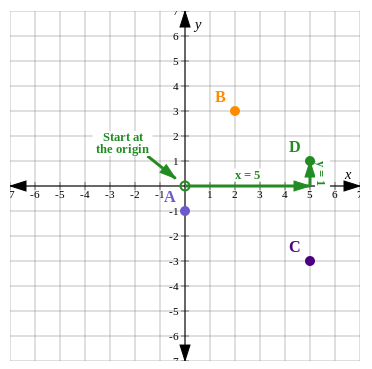
Write the final answer.
The point that has the coordinates \((5; 1)\) is point \(D\).
Worked example 23.4: Finding the coordinates of a given point
The diagram shows the Cartesian plane and two points. The points are labelled \(A\) and \(B\). Write down the coordinates of \(A\) and \(B\).
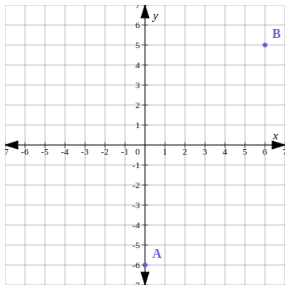
Read the coordinates from the axes for point B.
We need to find the \(x\)-value and the \(y\)-value which tell us the position of the point \(B\) from the origin.
- To find the \(x\)-value, we read how many units on the \(x\)-axis point \(B\) is from the origin (the red arrow in the diagram). The \(x\)-coordinate is \(6\).
- To find the \(y\)-value, we read how many units on the \(y\)-axis point \(B\) is from the origin (the red arrow in the diagram). The \(y\)-coordinate is \(5\).
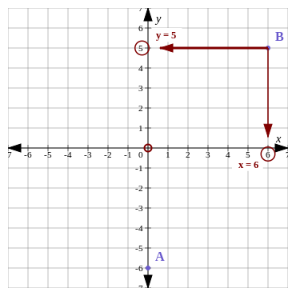
Notice that the value of the \(x\)-coordinate shows that the point lies to the left or to the right of the origin. The value of the \(y\)-coordinate shows that the point lies above or below the origin.
Remember the order of coordinate pairs: \((x; y)\). The \(x\)-coordinate is first and the \(y\)-coordinate is second.
The coordinates of point \(B\) are: \((6; 5)\).
Read the coordinates from the axes for point A.
We notice that \(A\) lies on the \(y\)-axis. For any point that lies on the \(y\)-axis, the value of the \(x\)-coordinate is \(0\). So the coordinates of point \(A\) are: \((0; -6)\).
Write the final answer.
The coordinates of point \(A\) are \((0; -6)\) and point \(B\) are \((6; 5)\).
