2.5 Solving problems
Knowing how to order and compare integers will help you solve many everyday problems. You can compare different temperatures, understand bank accounts better, and work with distances between objects around you.
Worked example 2.18: Solving problems using counting and ordering
At a high school in Amajuba, there is a water tank, a classroom and a sports field. A student named Olwethu, who must have been bored, drew a number line on the ground all the way across the school grounds – you can see it in the picture below. He also labelled the number line in metres. According to the number line, the sports field is at position \(0\) metres, the water tank is at \(45\) metres and Olwethu’s classroom is at \(105\) metres.
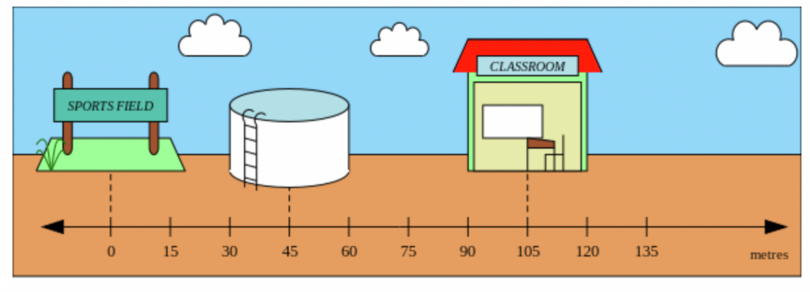
Olwethu walks from the water tank to his classroom, and then to the sports field.
What is the total distance that Olwethu walks?
Read the question carefully.
The question has a lot of information in it. It is important to read the question slowly and make sure that you feel like you have the story in your mind. Read the question a few times if you need to.
Draw a picture to represent the information.
A very good strategy for a question with a picture is to draw more information on this picture or draw a separate sketch to simplify the question.
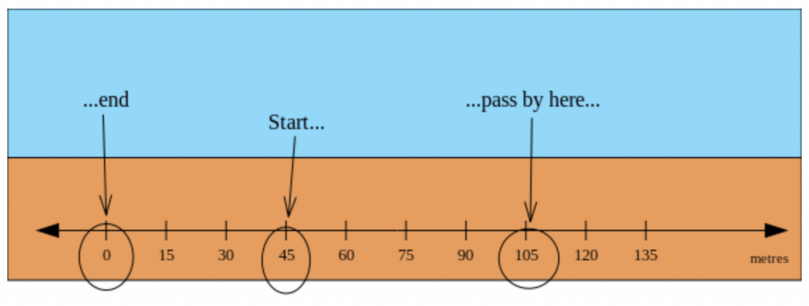
Calculate distances.
You can start by calculating the first distance from the starting position to the first place Olwethu passes. Remember that finding a distance means subtracting the smaller number from the larger number.
\[d_{\text{first}} = 105 - 45 = 60\]From the water tank to his classroom, the distance is 60 metres.
Next, find the distance for the second part of the question (from his classroom to the sports field):
\[d_{\text{second}} = 105 - 0 = 105\]The second part of the trip has a distance of 105 metres.
Calculate total distance.
Now add the two distances to get the total distance.
\[d_{\text{total}} = d_{\text{first}} + d_{\text{second}} = 60 + 105 = 165\ m\]Olwethu walked a total distance of \(165\) m.
Worked example 2.19: Solving problems using counting and ordering
Justine is in debt with her bank. Her balance is currently \(−600\) rand. If she spends a further \(100\) rand using the account, what will her new balance be?
Understand the problem.
Increase Justine’s debt by \(\text{R}100\).
Justine’s bank balance is currently \(−600\) rand. The negative balance means that she owes the bank money, so Justine owes the bank \(\text{R}600\).
Find the solution.
If she spends a further \(\text{R}100\), then the amount that she owes increases to \(\text{R}700\). Therefore, her bank balance will be \(−700\) rand.
We can write this as:
\[- 600 - 100 = - 700\]Worked example 2.20: Solving problems using counting and ordering
On a freezing winter’s day, the minimum temperature in Towoomba was \(- 6^\circ \text{C}\) and the minimum temperature in Sutherland was \(- 12^\circ \text{C}\).
Which town recorded the warmer temperature?
Draw and use a number line.
The minimum temperature in Towoomba was \(- 6^\circ \text{C}\) and the minimum temperature in Sutherland was \(- 12^\circ \text{C}\).
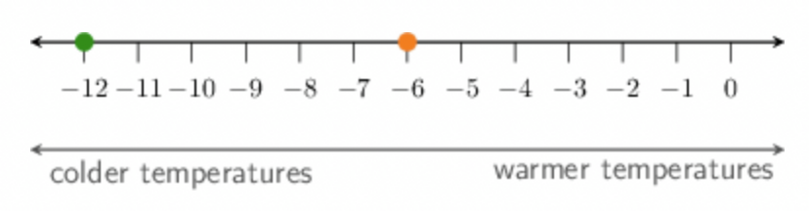
Compare the integers.
\[- 6 > - 12\]Smaller temperatures mean that it is colder; larger temperatures mean that it is warmer. Temperatures below zero are very cold and water will start to freeze.
Therefore, Towoomba recorded the warmer temperature.
