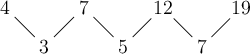
4.3 Investigating and extending geometric patterns
Kinds of geometric patterns
The patterns that you see in nature are often studied and represented using diagrams and numbers. This helps to understand how the pattern changes and to make predictions about these patterns.
Geometric patterns are number patterns that are represented diagrammatically. A diagrammatic representation reveals the structure of the number pattern.
- geometric pattern
- a pattern made of shapes; the pattern represents a number pattern
Let’s look at some familiar types of number patterns and how these could be represented diagrammatically.
Square numbers
In algebra, we think of a square as a number that is obtained by multiplying a number by itself. So, 1 is also a square because \(1 \times 1 = 1\).
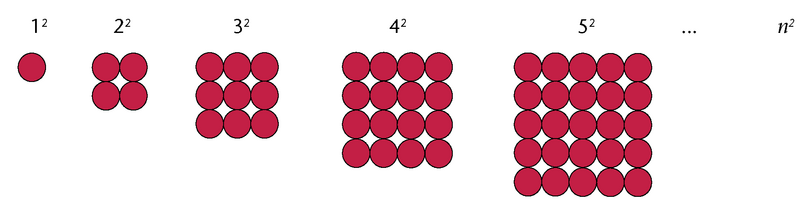
The symbol \(n\) is used to represent the position of a number in the expression that gives the rule (\(n^{2}\)) when generalising.
Triangular numbers
More than \(2 500\) years ago, Greek mathematicians discovered that the numbers \(3, 6, 10, 15\) and so on could form a triangular pattern. They represented these numbers using dots that they arranged in such a way that they formed equilateral triangles, hence the name. Algebraically, we think of them as sums of consecutive natural numbers starting with \(1\).
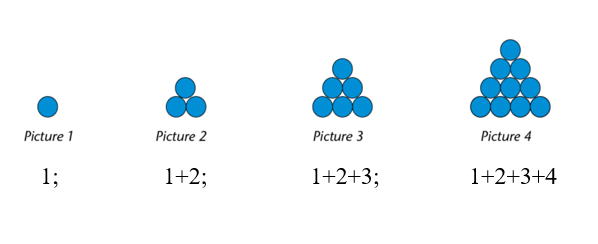
Rectangular numbers
If we double the number of circles in each picture above, we get a different arrangement:

We have added the yellow circles to the original blue circles and then rearranged the circles in such a way that they are in a rectangular form.
Picture \(1\) is \(2\) circles long and \(1\) circle wide = \(2\) circles
Picture \(2\) is \(3\) circles long and \(2\) circles wide = \(6\) circles
Picture \(3\) is \(4\) circles long and \(3\) circles wide = \(12\) circles
Picture \(4\) is \(5\) circles long and \(4\) circles wide = \(20\) circles
So, you can guess that picture \(20\) will be \(21\) circles long and \(20\) circles wide, giving a total of \(21 \times 20 = 420\) circles.
Worked example 4.12: Building patterns with shapes
Abdoul is building patterns with matchsticks. He builds one pattern each day. Here are the first four constructions:
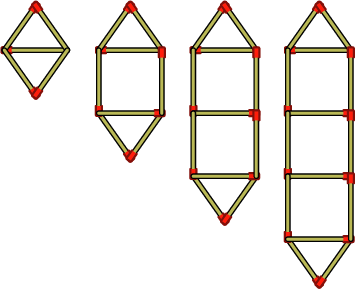
How many matchsticks does Abdoul use on the fifth day?
Count the number of matches in each construction.
To get the next item in the pattern, Abdoul adds three matchsticks to the previous item.
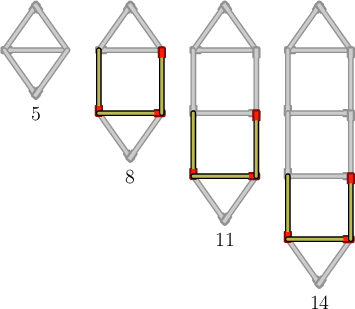
Determine the number of matches in the fifth construction.
The fifth construction will have three more matches than the fourth construction:
\[14 + 3 = 17\]Therefore, Abdoul will use \(17\) matches on the fifth day.
Worked example 4.13: Building patterns with shapes
Consider the following pattern:
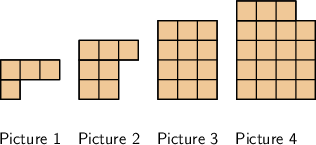
How many squares there will be in the \(7\)th picture?
Count the number of squares in each picture.
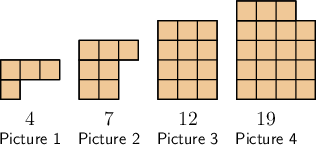
There are \(19\) squares in Picture \(4\).
Continue the pattern to find the number of squares in the fifth picture.
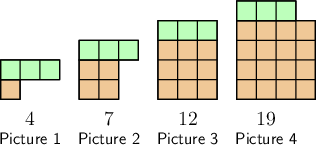
The first picture has one row of one square, plus three squares on top. The second picture has two rows of two squares, plus three squares on top, and so on. So, the fifth picture will have five rows of five squares, plus three squares on top. Therefore, the fifth picture will have \(28\) squares:

You could also answer this question by looking at the pattern in the differences between the terms:
The differences increase by \(2\) each time. So, the next difference will be \(9\). \(19 + 9 = 28\), so this method also gives an answer of \(28\) squares.
Find the number of squares in \(6\)th and \(7\)th pictures.
We can look at the pattern in the differences between each term. The differences increase by \(2\) each time, and we can use this fact to continue the pattern:

Therefore, there will be \(52\) squares in the \(7\)th picture.