26.3 Theoretical probabilities
Probability is a mathematical way of describing how likely an event is to occur. To describe the probability that something will happen, we can use a probability scale. This scale is a continuous line that starts with impossible events at the left-hand end and ends with certain events at the right-hand end. All probabilities must fall somewhere on this line.
An event that is described as “impossible” is one that we know will never happen, such as having eight days in one week.
An event is described as “certain” if we know that it will definitely happen, such as Sunday coming after Saturday.
Between the two ends of the line are word descriptions: very unlikely, unlikely, even chance, likely, very likely.
Remember that each word description covers a range of continuous probabilities on the scale, and it doesn’t match a particular number exactly. The word descriptions used describe the mathematical meaning.
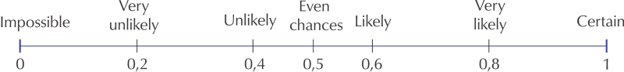
We can also give numbers to the probabilities on this scale. A probability is a real number between \(0\) and \(1\) that describes how likely it is that an event will occur.

We can describe probabilities in three ways:
- As decimal fractions between \(0\) and \(1\).
For example, \(\text{0,25}\) or \(\text{0,75}\). - As percentages between \(0 \%\) and \(100 \%\).
For example, \(\text{0,25}\) can be written as \(25\%\). and \(\text{0,75}\) can be written as \(75\%\). - As fractions between \(0\) and \(1\).
For example, \(\text{0,25}\) can also be written as \(\frac{1}{4}\) and \(\text{0,75}\) can also be written as \(\frac{3}{4}\).
Worked example 26.1: Calculating simple probabilities
- What is the probability of getting a red button from a bag that contains \(8\) blue buttons?
- A box contains \(2\) tennis balls and \(2\) cricket balls. What is the probability of picking a tennis ball?
- What is the probability of getting a number less than \(7\) when you through a dice?
Calculate the probability of getting a red button.
The bag contains \(8\) blue buttons and \(0\) red buttons, so there is no chance of getting a red
button.
The probability of getting a red button is \(\frac{0}{8} = 0\).
We call this an impossible event.
Calculate the probability of picking a tennis ball.
A box contains \(2\) tennis balls and \(2\) cricket balls. There are a total of \(4\) balls in the box.
The probability of picking a tennis ball is \(\frac{2}{4} = \frac{1}{2}\). We could also express this as a decimal, \(\text{0,5}\), or as a percentage, \(50\%\).
There is an even chance of getting a tennis ball or a cricket ball.
Calculate the probability of getting a number less than \(7\).
A dice has six sides with numbers from \(1\) to \(6\). So all the numbers on a dice are less than \(7\).
The probability of getting a number less than \(7\) is: \(\frac{7}{7} = 1\) or \(100\%\).
We call this a certain event.
Calculating the probability of an event
When all of the possible outcomes of an experiment have an equal chance of occurring, we can calculate the probability of an event. The probability of an event is the number of outcomes in the event set divided by the number of possible outcomes in the sample space.
For example: There are seven days in the week {Monday, Tuesday, Wednesday, Thursday, Friday, Saturday and Sunday}. Two days of the week begin with the letter ‘S’.
Suppose we randomly picked a day of the week and wanted to know the probability of picking a day that starts with the letter ‘S’.
In this case, the number of outcomes in the even set is \(2\) (Saturday and Sunday).
The number of possible outcomes in the sample space is the number of days in the week, \(7\).
So the probability of picking a day that starts with the letter ‘S’ is: \(\frac{2}{7}\).
So the formula is:
\[P(E) = \frac{n(E)}{n(S)}\]Worked example 26.2: Calculating probabilities for rolling a dice
What is the probability of getting a number greater than \(4\) when you roll a dice?
Write down the number of possible outcomes in the sample space.
The number of possible outcomes in the sample space is equal to the number of faces on the dice.
\[n(S) = 6\]Write down the number of outcomes in the event set.
The number of outcomes in the event space is equal to the number of faces on the dice that have a value greater than \(4\). There are only two possibilities here: \(5\) and \(6\).
\[n(E) = 2\]Calculate the probability.
\(P(E) = \frac{n(E)}{n(S)}\) \(= \frac{2}{6}\) \(= \frac{1}{3}\) \(= \text{0,33}\)
Worked example 26.3: Calculating probabilities for drawing a card from a pack
What is the probability of getting a queen when you draw a single card at random from a pack of cards? Give your answer as a percentage.
Write down the number of possible outcomes in the sample space.
The number of possible outcomes in the sample space is equal to the number of cards in the pack:
\[n(S) = 52\]Write down the number of outcomes in the event set.
The event contains four possible outcomes: \(E = {Q\heartsuit; Q\clubsuit; Q\diamondsuit; Q\spadesuit}\).
So the number of outcomes in the event space is equal to the number of queen cards in the pack:
\[n(E) = 4\]