Use the theorem of Pythagoras to determine if the triangle is a right-angled triangle or not.

\(c^2 = a^2 + b^2\) (Pythagoras)
LHS \(= c^2 = 6^2 = 36\)
RHS \(= a^2 + b^2 = 4^2 + 4^2 = 16 + 16 = 32\)
Not a right-angled triangle
|
Previous
Surds
|
Next
Chapter summary
|
The theorem of Pythagoras is a rule that applies only to right-angled triangles. The side opposite the right angle of a right-angled triangle is called the hypotenuse. The hypotenuse is always the longest side of a right-angled triangle.
For this investigation, you will need a pencil, a ruler, a pair of scissors and two pieces of squared paper.
Read through all the instructions before you start the investigation.
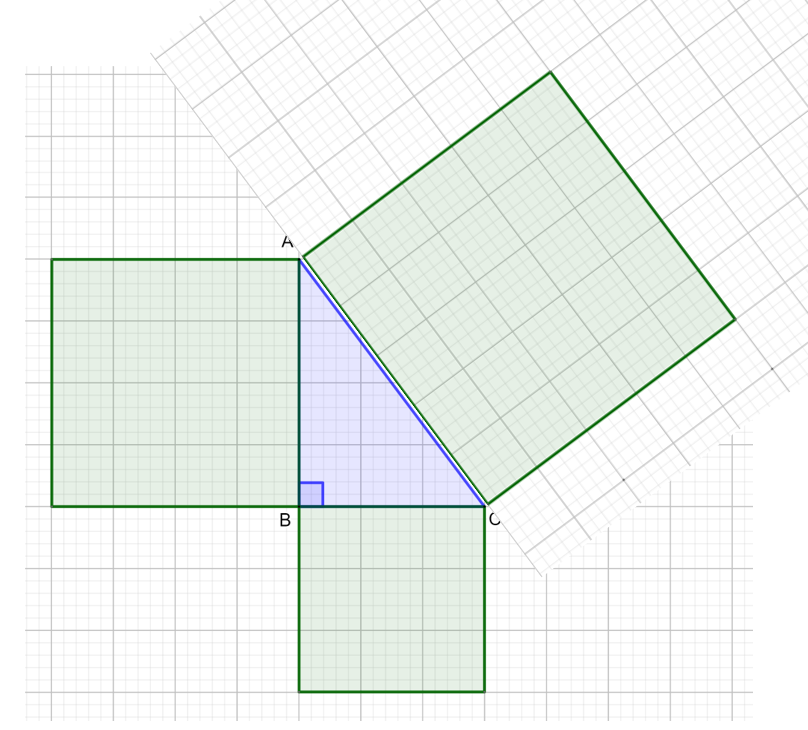
Use your diagram to complete the table for the area of each square:
| Area Square 1 | Area Square 2 | Area Square 1 + Area Square 2 | Area Square 3 |
|---|---|---|---|
Use your diagram to complete the table for the lengths of the sides of the triangle:
| \(AB\) | \(BC\) | \(AC\) | \(AB^2 + BC^2\) | \(AC^2\) |
|---|---|---|---|---|
Use your diagram to complete the table for the area of each square:
| Area Square 1 | Area Square 2 | Area Square 1 + Area Square 2 | Area Square 3 |
|---|---|---|---|
Use your diagram to complete the table for the lengths of the sides of the triangle:
| \(DE\) | \(EF\) | \(DF\) | \(DE^2 + EF^2\) | \(DF^2\) |
|---|---|---|---|---|
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two other sides.
\(c^2 = a^2 + b^2\) or \(a^2 + b^2 = c^2\)
If we know the lengths of all three sides of a triangle, we can use the theorem of Pythagoras to determine if the triangle is a right-angled triangle or not.
For the triangle below, \(z\) is the longest side of the triangle.
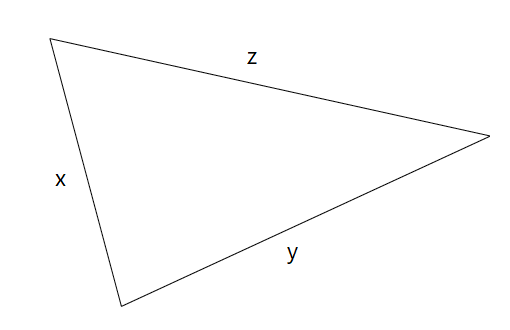
Use the theorem of Pythagoras to show that \(\triangle XYZ\) is a right-angled triangle.
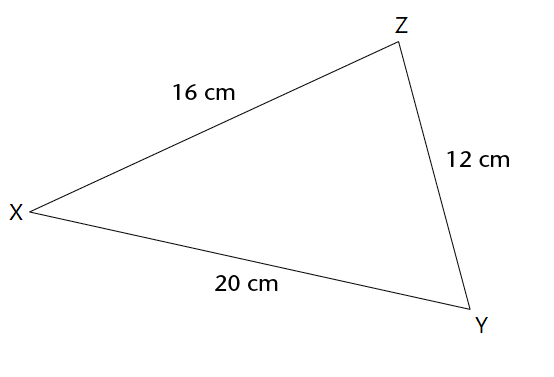
In \(\triangle XYZ\), \(XY = 20 \text{ cm}, YZ= 12 \text{ cm}\) and \(ZX = 16 \text{ cm}\). So the longest side is \(XY\), which means that if \(\triangle XYZ\) is a right-angled triangle, then \(XY\) is the hypotenuse.
In \(\triangle XYZ\),
\[\begin{align} XY^2 &= 20^2 \\ &= 400 \end{align}\] \[\begin{align} YZ^2 + ZX^2 &= 12^2 + 16^2 \\ &= 144 + 256 \\ &= 400 \end{align}\]We have shown that \(XY^2 = YZ^2 + ZX^2\)
This means that the theorem of Pythagoras holds true, so \(\triangle XYZ\) is a right-angled triangle.
\(\triangle XYZ\) is a right-angled triangle with \(\angle Z = 90^{\circ}\).
Use the theorem of Pythagoras to determine if the triangle is a right-angled triangle or not.

\(c^2 = a^2 + b^2\) (Pythagoras)
LHS \(= c^2 = 6^2 = 36\)
RHS \(= a^2 + b^2 = 4^2 + 4^2 = 16 + 16 = 32\)
Not a right-angled triangle
A triangle with sides \(4 \text{ units}, 15 \text{ units}\) and \(12 \text{ units}\) is shown. Is this a right-angled triangle? Show your calculations.

\(c^2 = a^2 + b^2\) (Pythagoras)
LHS: \(c^2 = 15^2 = 225\)
RHS: \(a^2 + b^2 = 4^2 + 12^2 = 16 + 144 = 160\)
Not a right-angled triangle
In each case the lengths of the three sides of a triangle are given. Determine whether the triangle is a right-angled triangle or not.
Use the theorem of Pythagoras to determine if the triangle is a right-angled triangle or not.

\(c^2 = a^2 + b^2\) (Pythagoras)
LHS \(= c^2 = 7^2 = 49\)
RHS \(= a^2 + b^2 = 3^2 + 5^2 = 9 + 25 = 34\)
Not a right-angled triangle
In \(\triangle KLM\), \(\angle L = 90^{\circ}\), \(KL = 8 \text{ cm}\) and \(LM = 6 \text{ cm}\).
Determine the length of \(KM\). Leave your answer in its simplest form.

\(\triangle KLM\) is a right-angled triangle, so we can use the theorem of Pythagoras to find the length of \(KM\). \(KM\) lies opposite the right angle, so \(KM\) is the hypotenuse.
\[\begin{align} KM^2 &= KL^2 + LM^2 \ (\text{Pythagoras}) \\ &= 8^2 + 6^2 \\ &= 64 + 36 \\ &= 100 \\ \therefore KM &= \sqrt{100} \\ &= 10 \end{align}\]Find \(y\). Give your answer in simplest surd form.
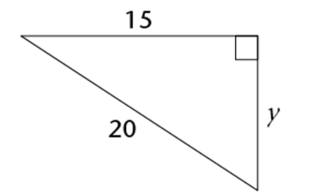
In this right-angled triangle, the hypotenuse is the side of length \(20 \text{ units}\).
\[20^2 = y^2 + 15^2\]Rearrange the equation to determine \(y\):
\[\begin{align} 20^2 − 15^2 &= y^2 \\ 400\ –\ 225 &= y^2 \\ 175 &= y^2 \end{align}\]Take the square root to calculate \(y\):
\[y = \sqrt{175}\]So, \(y = 5\sqrt{7} \text{ units}\)
|
Previous
Surds
|
Table of Contents |
Next
Chapter summary
|