 perpendicular lines.
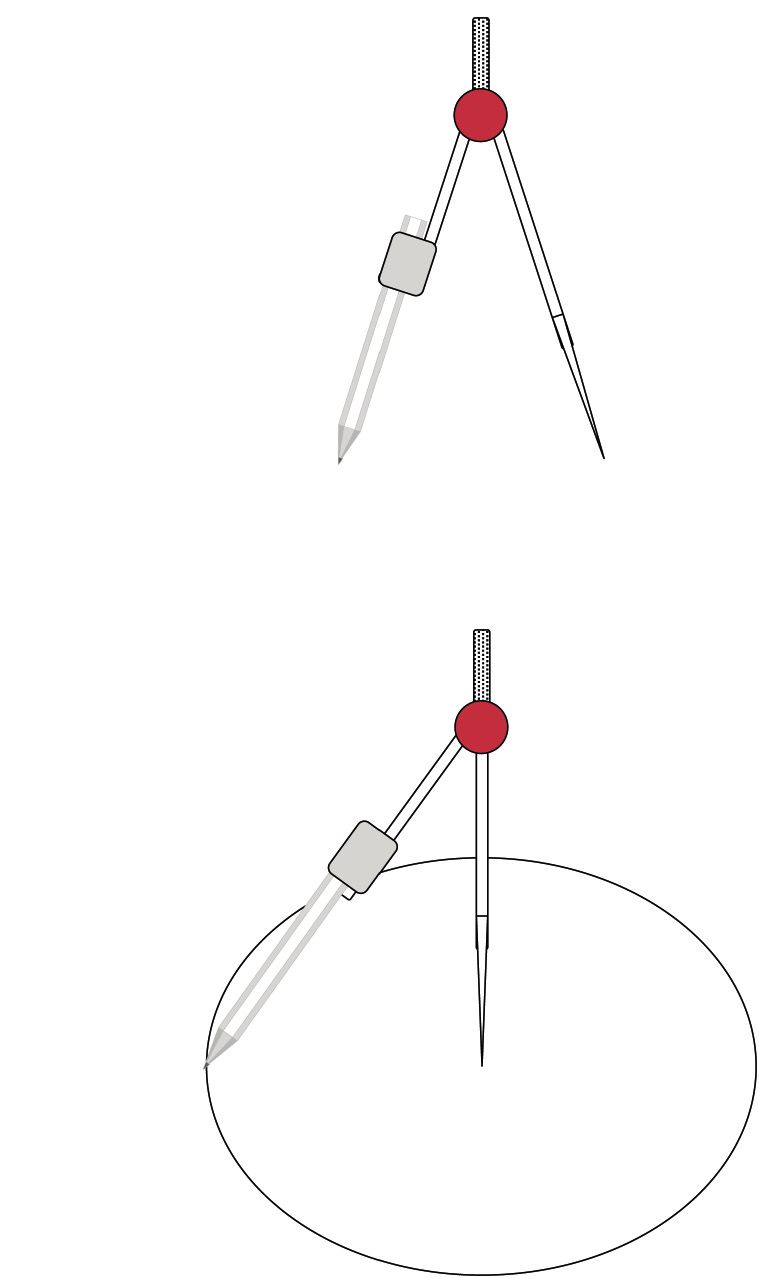
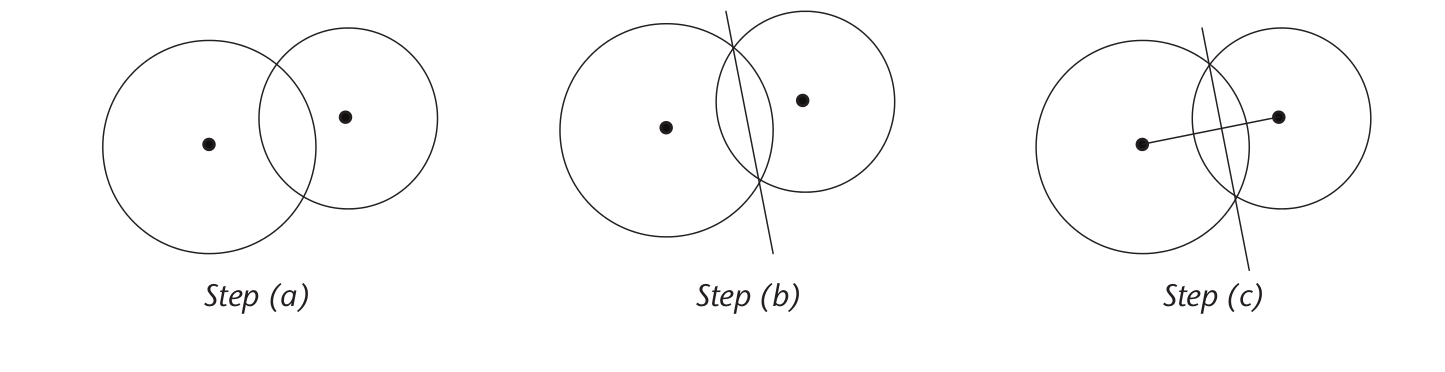
perpendicular lines.- Use a compass to draw two overlapping circles of different sizes.
- Draw a line through the points where the circles intersect (overlap).
- Draw a line to join the centres of the
circles.
- Use your protractor to
measure the angles between the intersecting lines.
- What can you say
about the intersecting lines?
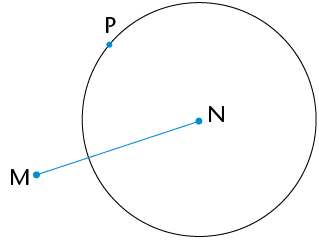
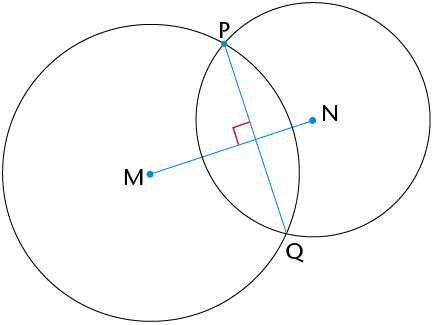
You are given line segment MN with point P at a distance from it. You must construct a line that is perpendicular to MN, so that the perpendicular passes through point P.

Step 1
Use your compass to draw a circle whose centre is the one end point of the line segment (N) and passes through the point (P).
Step 2
Repeat step 1, but make the centre of your circle the other end point of the line segment (M).

Step 3
Join the points where the circles intersect: PQ \(\perp \) MN
You are given line segment XY with point Z on it. You must construct a perpendicular line passing through Z.

Step 1
Use your compass to draw a circle whose centre is Z. Make its radius smaller than ZX. Note the two points where the circle intersects XY.

Step 2
Set your compass wider than it was for the circle with centre Z. Draw two circles of the same size whose centres are at the two pointswhere the first (black) circle intersects XY. The two circles (green) will overlap.

Step 3
Join the intersection points of the two overlapping circles. Mark these points C and D: CD \( \perp \) XY and passes through point Z.



The word bisect means 'to cut in half'.
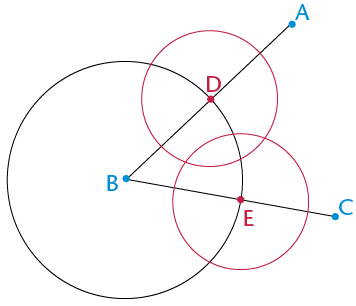
You are given \(\text{A}\hat{\text{B}}\text{C}\). You must bisect the angle.

Step 1
Draw a circle with centre B to mark off an equal length on both arms of the angle. Label the points of intersection D and E: DB = BE.

Step 2
Draw two equal circles with centres at D and at E. Make sure the circles overlap.
Step 3
Draw a line from B through the points where the two equal circles intersect. This line will bisect the angle.
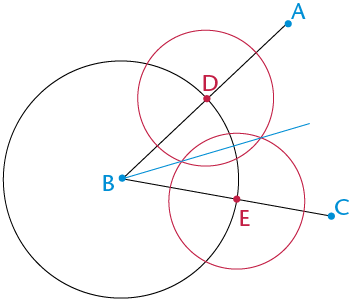
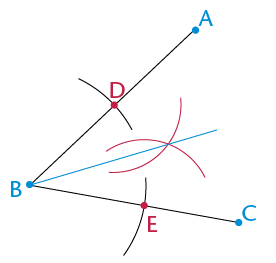
Can you explain why the method above works to bisect an angle?
Can you also see that we need not draw full circles, but can merely use parts of circles (arcs) to do the above construction?
 special angles. You must be able to construct these
angles without using a protractor.
special angles. You must be able to construct these
angles without using a protractor.Hint: Extend the line to the left of X.

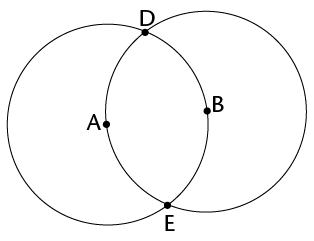
- The circles are the same size.
- Each circle passes through the other circle's centre.
- The centres of the circles are labelled A and B.
- The points of intersection of the circles are labelled D and E.
An example is shown here:
|
Angle |
Multiples below 360\(^\circ\) |
Angle |
Multiples below 360\(^\circ\) |
|
30\(^\circ\) |
30\(^\circ\); 60\(^\circ\); 90\(^\circ\); 120\(^\circ\); 150\(^\circ\); 180\(^\circ\); 210\(^\circ\); 240\(^\circ\); 270\(^\circ\); 300\(^\circ\); 330\(^\circ\) |
45\(^\circ\) |
|
|
60\(^\circ\) |
90\(^\circ\) |
- 120\(^\circ\)
- 135\(^\circ\)
- 270\(^\circ\)
- 240\(^\circ\)
- 150\(^\circ\)

- Bisect each of the angles of the acute triangle below.
- Extend each of the bisectors to the opposite side of the triangle.
- What do you notice?
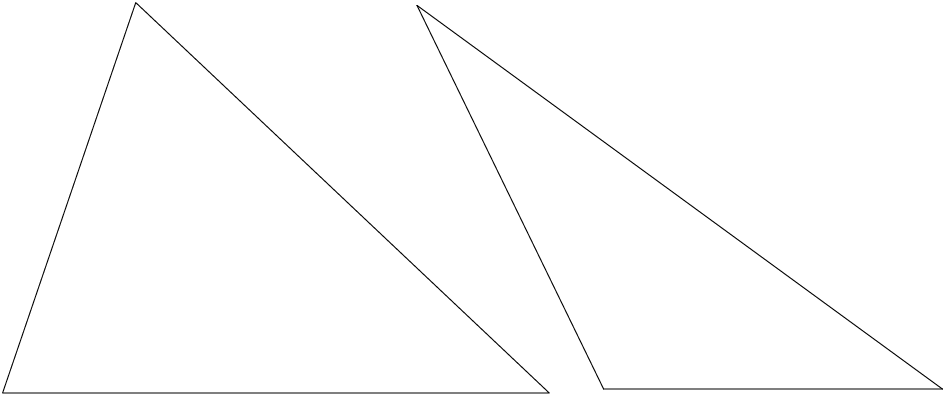
You should have found that the three angle bisectors of a triangle intersect at one point. This point is the same distance away from each side of the triangle.
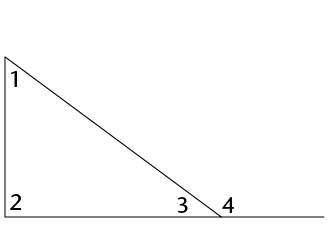
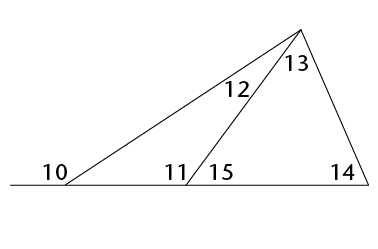
An interior angle is an angle that lies between two sides of a triangle. It is inside the triangle. A triangle has three interior angles.
An exterior angle is an angle between a side of a triangle and another side that is extended. It is outside the triangle.
 interior
opposite angles, as described in the following table.
interior
opposite angles, as described in the following table.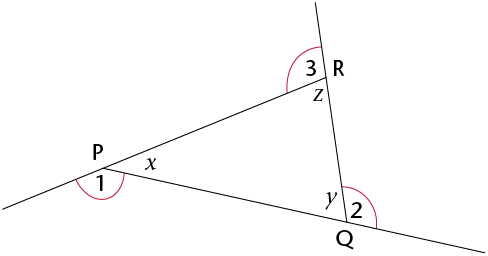
Exterior angle
Interior adjacent angle
Interior opposite angles
1
x
z and y
2
y
x and z
3
z
x and y
|
Ext. \(\angle\) |
|||||
|
Int. opp. \(\angle\)s |
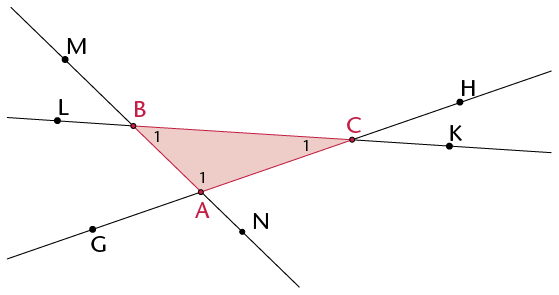
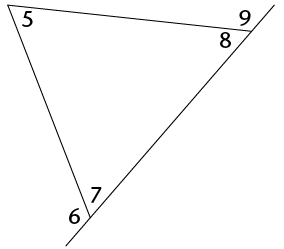
- Write down the names of the interior
angles of the triangle.
- Since a triangle has three sides that
can be extended in both directions, there are two exterior
angles at each vertex. Write down the names of all the exterior
angles of the triangle.
-
Explain why \(\text{M}\hat{\text{B}}\text{L}\) is not an exterior angle of \(\triangle\)ABC.
- Write down two other angles that are
neither interior nor exterior.
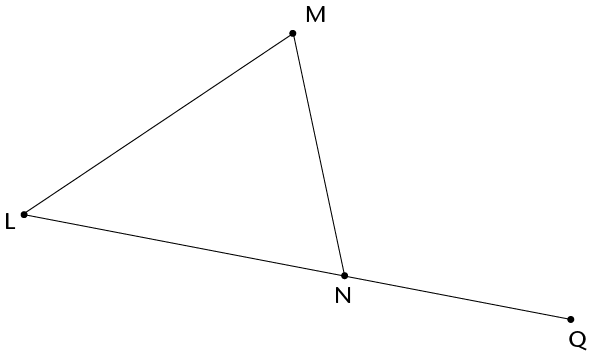
\(\text{L}\hat{\text{M}}\text{N} + \text{M}\hat{\text{L}}\text{N} = \)
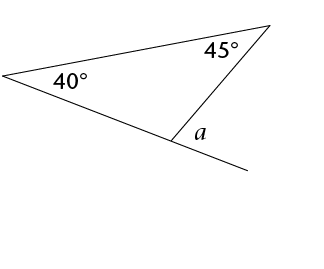
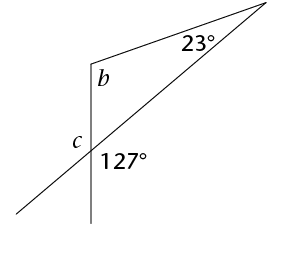
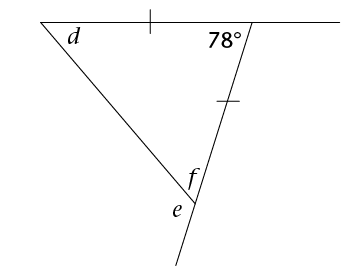
The exterior angle of a triangle is equal to the sum of the interior opposite angles.


- Given three sides: side, side, side (SSS):\(\triangle\)DEF with DE = 7 cm, DF = 6 cm and EF = 5 cm.
- Given three angles: angle, angle, angle (AAA): \(\triangle\)ABC with \(\hat{\text{A}} = 80^\circ, \hat{\text{B}} = 60^\circ, \hat{\text{C}} = 40^\circ\)
- Given one side and two angles: side, angle, angle (SAA): \(\triangle\)GHI with \(\text{GH} = 8 \text{ cm}\), \(\hat{\text{G}} = 60^\circ, \hat{\text{H}} = 30^\circ\)
- Given two sides and an included angle: side, angle, side (SAS): \(\triangle\)JKL with JK =9 cm, \(\hat{\text{K}}=\) 130\(^\circ\) and KL = 7 cm.
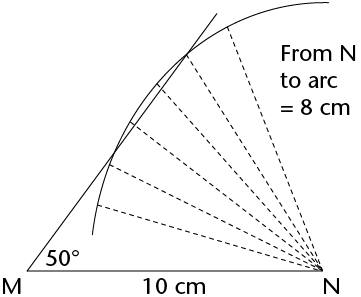
- Given two sides and an angle that is not included: side, side, angle (SSA):\(\triangle\)MNP with MN = 10 cm, \(\hat{\text{M}}=\) = 50\(^\circ\) and PN = 8 cm.
- Given a right angle, the hypotenuse and a side (RHS):\(\triangle\)TRS with TR \(\perp\) RS, RS = 7 cm and TS = 8 cm.
- Triangle UVW with UV = 6 cm and VW = 4 cm.
|
Step 1 Construct MN = 10 cm and the 50\(^\circ\) angle at M, even though you do not know the length of unknown side (MP).
|
Step 2 \(\hat{N}\) is unknown, but NP = 8 cm. So construct an arc 8 cm from N. Every point on the arc is 8 cm from N.
|
|
Step 3 Point P must be 8 cm from N and fall on the unknown side of the triangle. The arc intersects the third side at two points, so P can be at either point. So two triangles are possible, each meeting the conditions given, i.e. MN = 10 cm, NP = 8 cm and \(\hat{M}\) = 50\(^\circ\).  |
|
|
Conditions |
Congruent? |
|
3 sides (SSS) |
|
|
2 sides (SS) |
|
|
3 angles (AAA) |
|
|
2 angles and a side (AAS) |
|
|
2 sides and an angle not between the sides (SSA) |
|
|
2 sides and an angle between the sides (SAS) |
|
|
Right-angled with the hypotenuse and a side (RHS) |
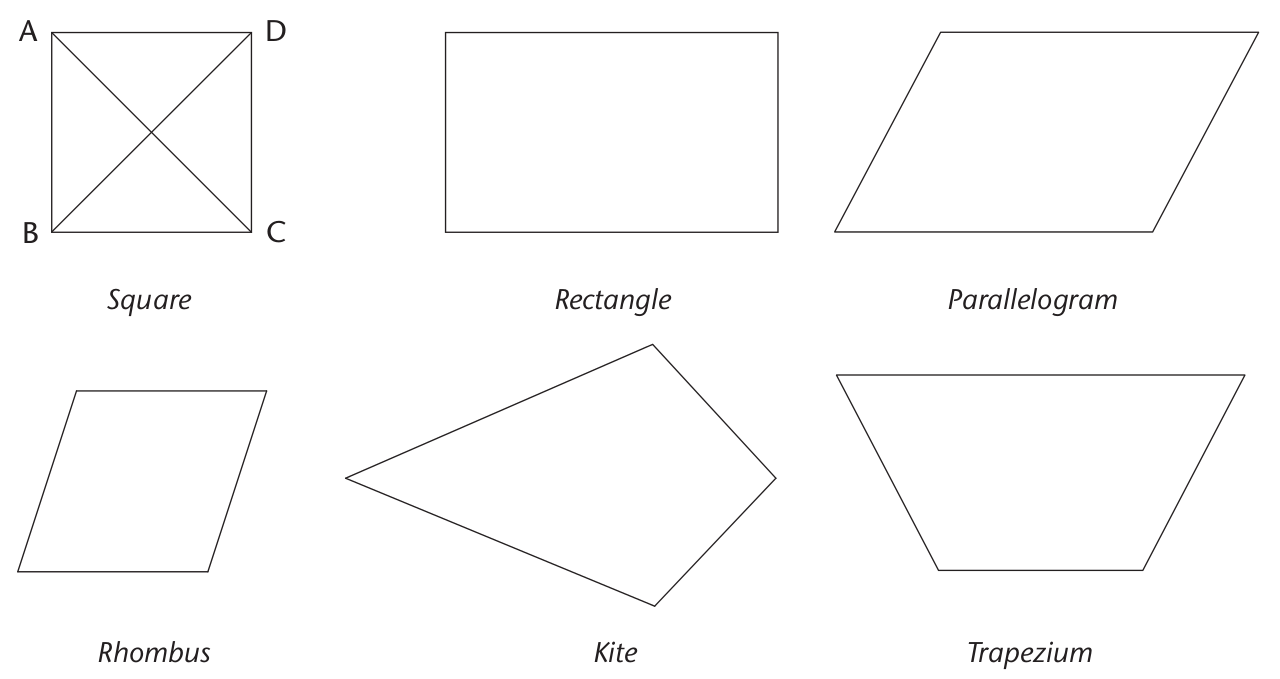
A perpendicular bisector is a line that cuts another line in half at a right angle (90\(^\circ\)).

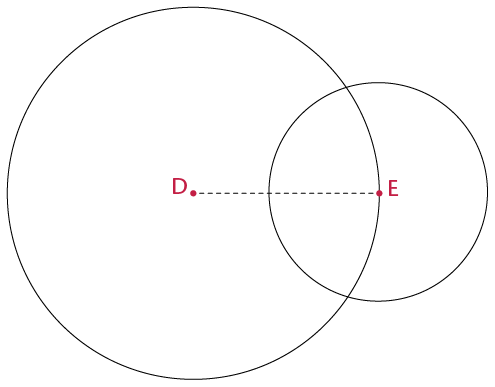

|
Quadrilateral |
Diagonals equal |
Diagonals bisect |
Diagonals meet at 90\(^\circ\) |
|
Parallelogram |
|||
|
Rectangle |
|||
|
Square |
- Draw in diagonals to divide each of the other polygons below into as few triangles as possible.
- Write down the number of triangles in each polygon.
Quadrilateral
Pentagon
Hexagon
No. of \(\triangle\)s
2
Sum of \(\angle\)s
2 \times 180\(^\circ\) = 360\(^\circ\)
Heptagon
Octagon
Nonagon
No. of \(\triangle\)s
Sum of \(\angle\)s
- Match the words in the column on
the right with the definitions on the left. Write the letter of
the definition next to the matching word.
(a) A quadrilateral that has diagonals that are perpendicular and they bisect each other
Kite
(b) A quadrilateral that has diagonals that are perpendicular to each other, and only one diagonal bisects the other
Congruent
(c) A quadrilateral that has equal diagonals that bisect each other
Exterior angle
(d) Figures that have exactly the same size and shape
Rhombus
(e) Divides into two equal parts
Perpendicular
(f) An angle that is formed outside a closed shape: it is between the side of the shape and a side that has been extended
Bisect
(g) Lines that intersect at 90 degrees
Special angles
(h) 90\(^\circ\), 45\(^\circ\), 30\(^\circ\), 60\(^\circ\)
Rectangle
- Complete
the sentence: The exterior angle in a triangle is equal to
-
- Construct \(\triangle\)PQR below with angles of 30\(^\circ\) and 60\(^\circ\). The side between the angles must be 8 cm. You may use only a ruler and a compass.
- Will all triangles with the same measurements above be congruent to
\(\triangle\)PQR? Explain
your answer.