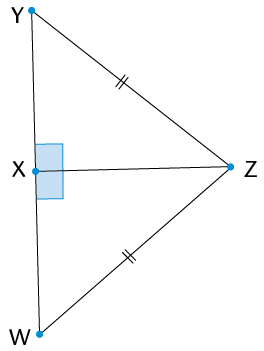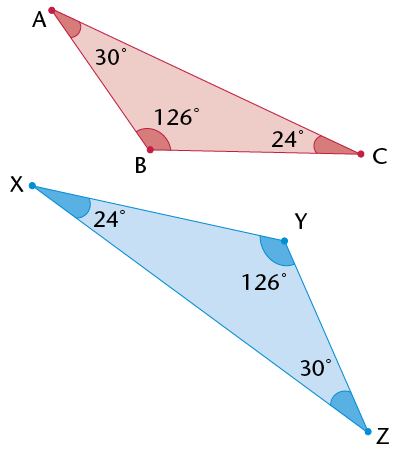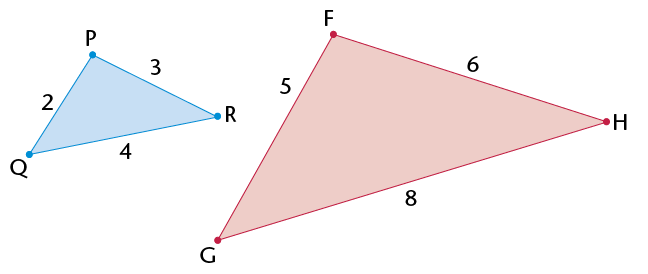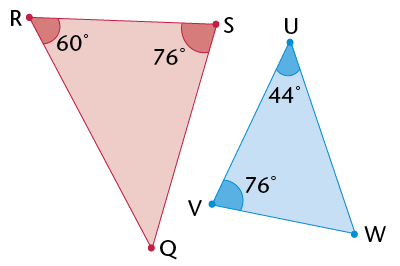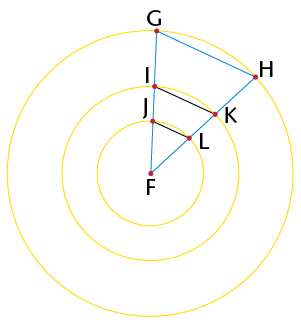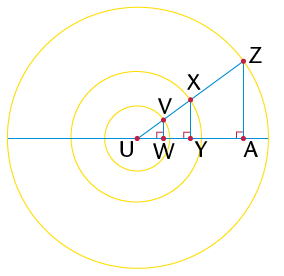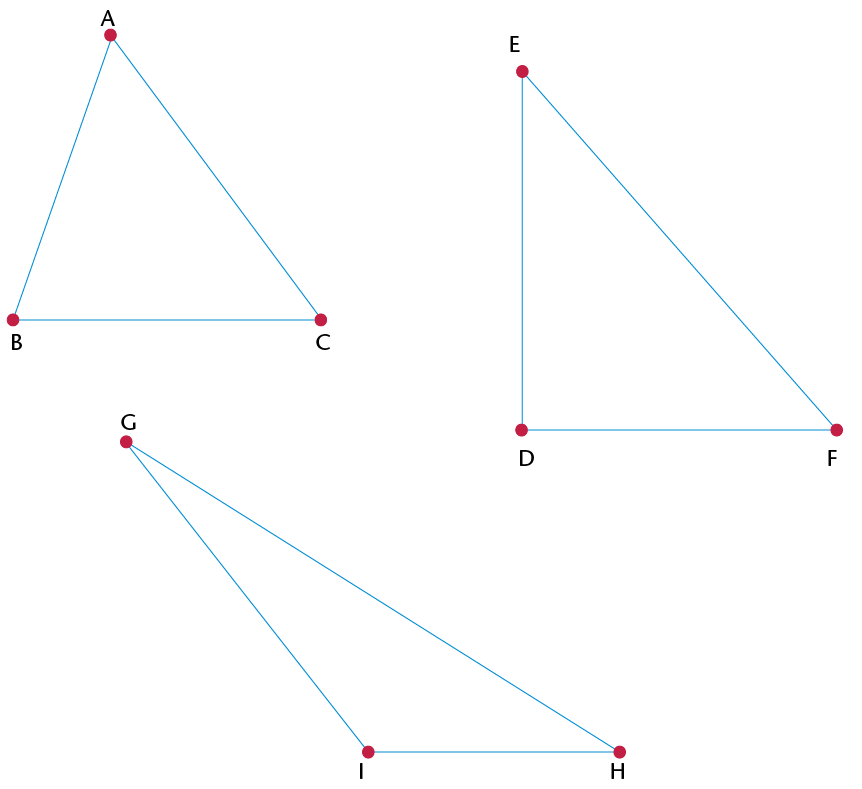
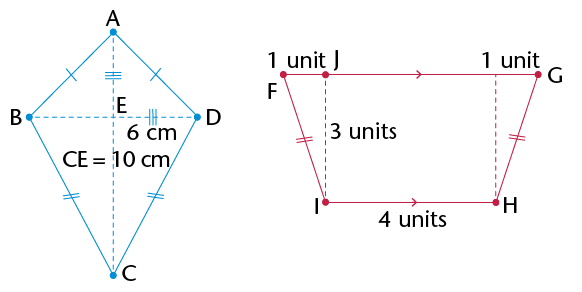
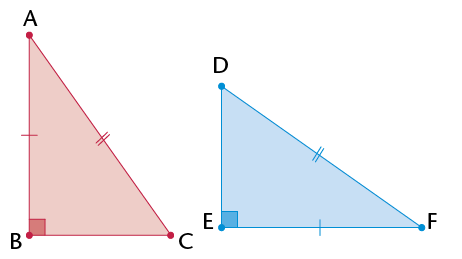
- \(\triangle\)ABC is an
_______
triangle, because
- \(\triangle\)EDF is a
_______ triangle, because
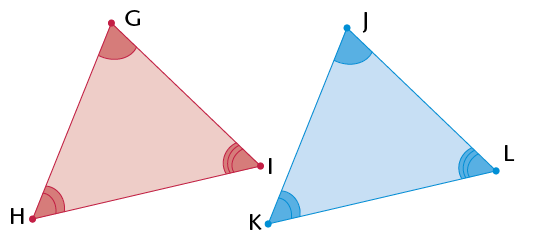
- \(\triangle\)GHI is an
obtuse-angled triangle, because
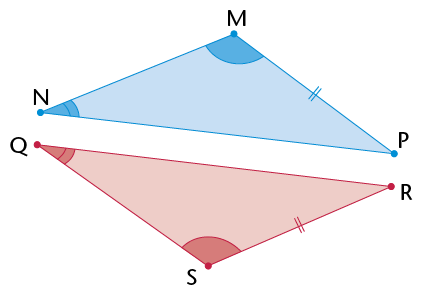
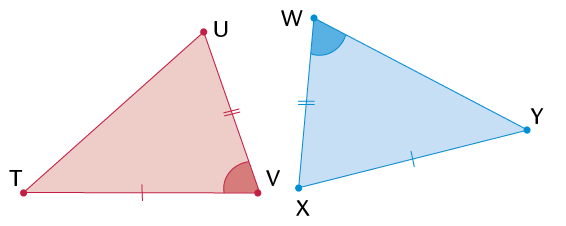
- \(\triangle\) .......... is an acute isosceles triangle, because ........ and .........
- \(\triangle\) .......... is a right-angled isosceles triangle, because ......... and ........
- \(\triangle\) .......... is an obtuse isosceles triangle, because ........... and ..........
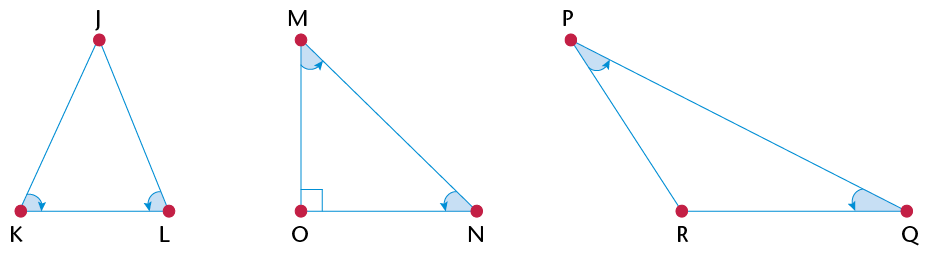
|
Statement |
True for |
|
|
(a) |
Two sides of the triangle are equal. |
|
|
(b) |
One angle of the triangle is obtuse. |
|
|
(c) |
Two angles of the triangle are equal. |
|
|
(d) |
All three angles of the triangle are equal to 60\(^\circ\). |
|
|
(e) |
The size of an exterior angle is equal to the sum of the opposite interior angles. |
|
|
(f) |
The longest side of the triangle is opposite the biggest angle. |
|
|
(g) |
The sum of the two shorter sides of the triangle is bigger than the length of the longest side. |
|
|
(h) |
The square of the length of one side is equal to the sum of the squares of the other sides. |
|
|
(i) |
The square of the length of one side is bigger than the sum of the squares of the other sides. |
|
|
(j) |
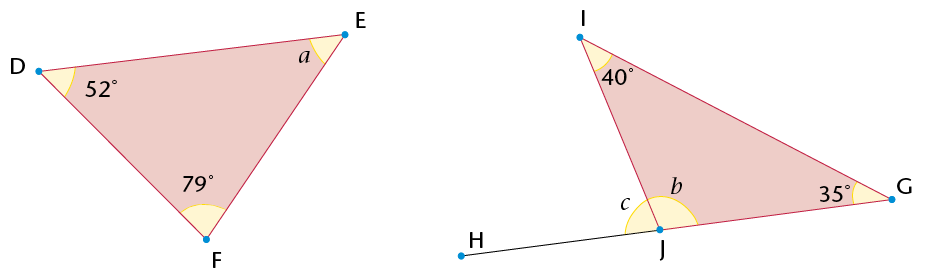
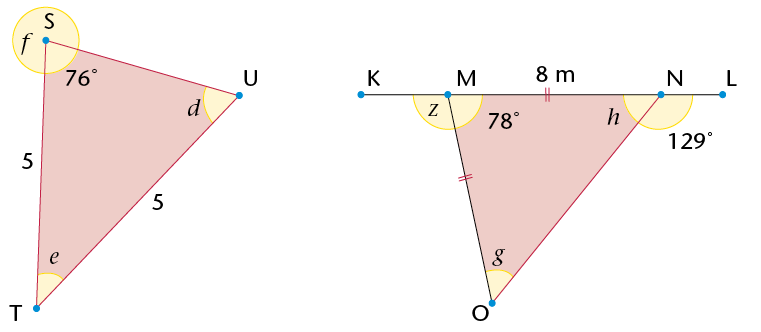
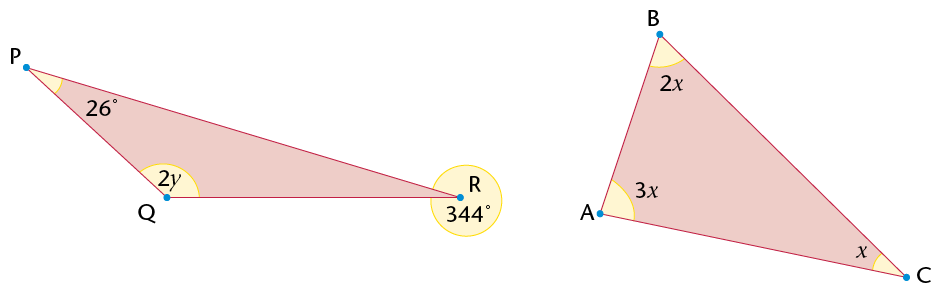
The sum of the interior angles of the triangle is 180\(^\circ\). |





|
Properties |
True for the following quadrilaterals |
|||||
|
Square |
Rhombus |
Rectangle |
Parallelogram |
Kite |
Trapezium |
|
|
At least one pair of opposite angles is equal. |
yes |
yes |
yes |
yes |
yes |
no |
|
Both pairs of opposite angles are equal. |
||||||
|
At least one pair of adjacent angles is equal. |
||||||
|
All four angles are equal. |
||||||
|
Any two opposite sides are equal. |
||||||
|
Two adjacent sides are equal, and the other two adjacent sides are also equal. |
||||||
|
All four sides are equal. |
||||||
|
At least one pair of opposite sides is parallel. |
||||||
|
Any two opposite sides are parallel. |
||||||
|
The two diagonals are perpendicular. |
||||||
|
At least one diagonal bisects the other one. |
||||||
|
The two diagonals bisect each other. |
||||||
|
The two diagonals are equal. |
||||||
|
At least one diagonal bisects a pair of opposite angles. |
||||||
|
Both diagonals bisect a pair of opposite angles. |
||||||
|
The sum of the interior angles is 360\(^\circ\). |
||||||
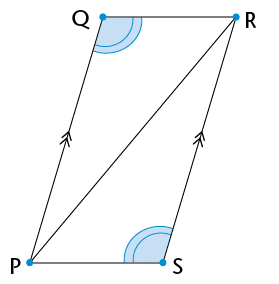
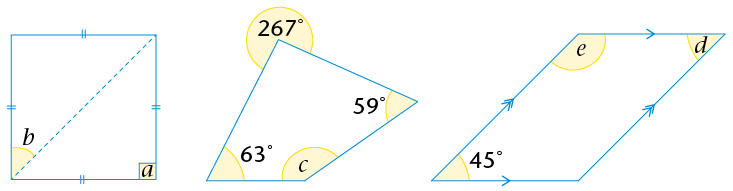
- Are all the properties of a square also
the properties of a rhombus? Explain.
- Are all the properties of a rhombus also
the properties of a square? Explain.
- Which statement is
true?
A square is a special kind of rhombus.
A rhombus is a special kind of square.
- Are all the properties of a square also
the properties of a rectangle? Explain.
- Are all the properties of a rectangle also
the properties of a square? Explain.
- Which statement is
true?
A square is a special kind of rectangle.
A rectangle is a special kind of square.
- Are all the properties of a parallelogram also
the properties of a rectangle? Explain.
- Are all the properties of a rectangle also
the properties of a parallelogram? Explain.
- Which statement is
true?
A parallelogram is a special kind of rectangle.
A rectangle is a special kind of parallelogram.
If you know that two triangles are congruent, then each side in the one triangle will be equal to each corresponding side in the second triangle. Also, each angle in the one triangle will be equal to each corresponding angle in the second triangle.
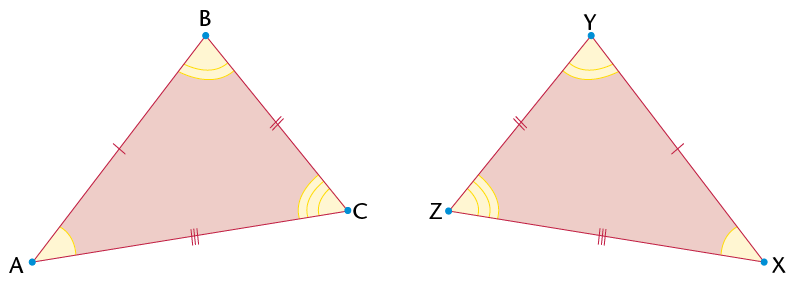 \(\equiv\)
\(\triangle\)XYZ.
\(\equiv\)
\(\triangle\)XYZ.Congruency symbol
\(\equiv\) means 'is congruent to'
The conditions for congruency:
- SSS (all corresponding sides are equal)
- SAS (two corresponding sides and the angle between the two sides are equal)
- AAS (two corresponding angles and any corresponding side are equal)
- RHS (both triangles have a \(90^\circ\) angle and have equal hypotenuses and one other side equal)

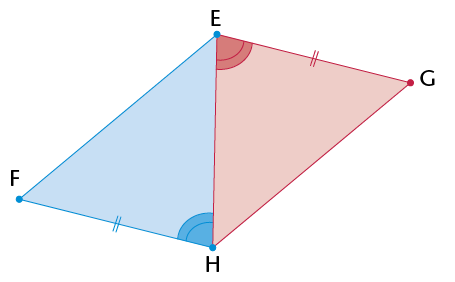
- Each statement you make needs a reason.
- You must give three statements to prove any two triangles congruent.
- Give the reason for congruency.
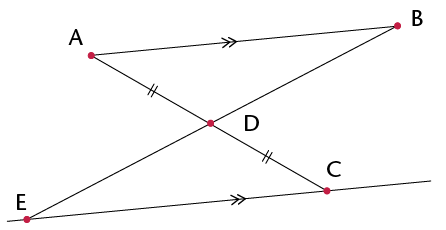 Solution:
Solution:
Statement
Reason
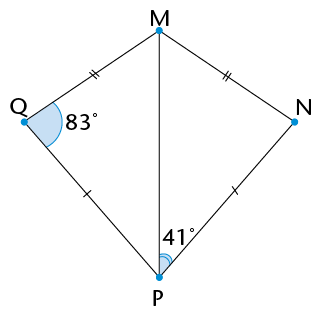
In \(\triangle\)ABD and \(\triangle\)CED:
1) AD = DC
2) \(\text{A}\hat{\text{D}}\text{B} = \text{C}\hat{\text{D}}\text{E}\)
3) \(\text{B}\hat{\text{A}}\text{D} = \text{E}\hat{\text{C}}\text{D}\)
\(\therefore\) \(\triangle\)ABD \(\equiv\) \(\triangle\)CED
Given
Vert. opp. \(\angle\)s
Alt. \(\angle\)s (AB\(||\) EC)
AAS
|
|
Statement |
Reason |
|
|
|
|
|
Statement |
Reason |
|
|
|
|
|
Statement |
Reason |
|
|
|
|
|
Statement |
Reason |
|
|
|
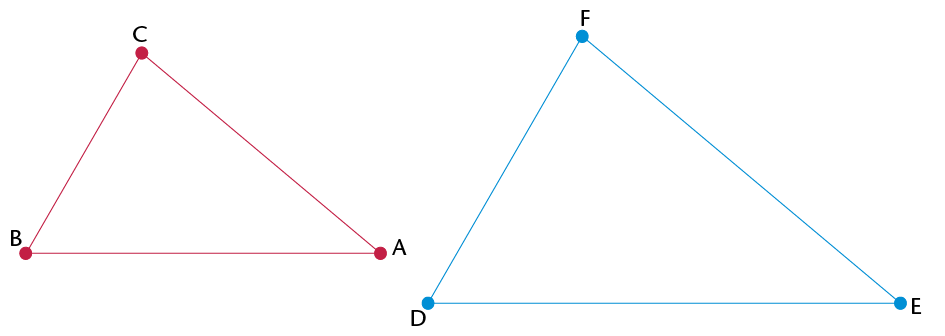
- Use a
protractor to measure the angles in each triangle above. Then
complete the table below.
Angle
Angle
What do you notice?
\(\hat{\text{B}} =\quad\)
\(\hat{\text{D}} =\)
\(\hat{\text{A}} =\)
\(\hat{\text{E}} =\)
\(\hat{\text{C}} =\)
>\(\hat{\text{F}} =\quad\)
- What can you say about the sizes of the
angles in similar triangles?
-
Use a ruler to measure the lengths of
the sides in each triangle in question 1. Then complete the
table below.
Length (cm)
Length (cm)
Ratio
BA =
DE =
BA : DE = \(\quad\) = \(1 : 1\frac{1}{3}\)
BC =
DF =
BC : DF = \(\quad\) = \(\quad\)
CA =
FE =
CA : FE = \(\quad\) = \(\quad\)
- What can you say about the relationship
between the sides in similar triangles?
Ratio reminder
You read 2 : 1 as 'two to one'.
-
The following notation shows that the triangles are similar: \(\triangle\)BAC \(|||\) \(\triangle\)DEF. Why do you think we write the first triangle as \(\triangle\)BAC and not as \(\triangle\)ABC?
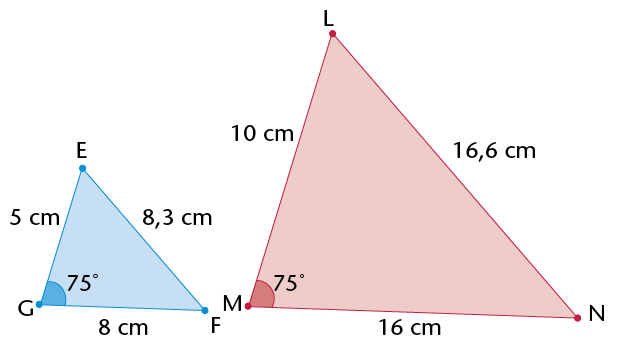
The properties of similar triangles:
- The corresponding angles are equal.
- The corresponding sides are in proportion.
Notation for similar triangles:
If \(\triangle\)XYZ is similar to \(\triangle\)PQR, then we write: \(\triangle\)XYZ \(|||\) \(\triangle\)PQR.
Angles: \(\hat{\text{X}} = \hat{\text{P}}\) and \(\hat{\text{Y}} = \hat{\text{Q}}\) and \(\hat{\text{Z}} = \hat{\text{R}}\)
Sides: \(\text{X}\)\(\text{Y}\):\(\text{P}\)\(\text{Q}=\text{X}\)\(\text{Z}\): \(\text{P}\)\(\text{R}=\text{Y}\)\(\text{Z}\):\(\text{Q}\)\(\text{R}\)
When proving that triangles are similar, you either need to show that the corresponding angles are equal or you must show that the sides are in proportion.
- Use a ruler and protractor to construct the triangles described in (a) to (d) below.
- Use your knowledge of similarity to draw the second triangle in each question.
- Indicate the sizes of the corresponding sides and angles on the second triangle.
- In \(\triangle\)EFG, \(\hat{\text{G}}\)= 75\(^\circ\), EG = 4 cm and GF = 5 cm. \(\triangle\)ABC is an enlargement of \(\triangle\)EFG, with its sides three times longer.
- In \(\triangle\)MNO, \(\hat{\text{M}}\)= 45\(^\circ\), \(\hat{\text{N}}\)= 30\(^\circ\) and MN = 5 cm. \(\triangle\)PQR is similar to \(\triangle\)MNO. The sides of \(\triangle\)MNO to \(\triangle\)PQR are in proportion 1 : 3.
- \(\triangle\)RST is an isosceles triangle. \(\hat{\text{R}}\)= 40\(^\circ\), RS is 10 cm and RS = RT. \(\triangle\)VWX is similar to \(\triangle\)RST. The sides of \(\triangle\)RST to \(\triangle\)VWX are in proportion 1:\(\frac{1}{2}\).
- \(\triangle\)KLM is right-angled at \(\hat{\text{L}}\), LM is 7 cm and the hypotenuse is 12 cm. \(\triangle\)XYZ is similar to \(\triangle\)KLM, so that the sides are a third of the length of \(\triangle\)KLM.
-
Which of the following are minimum conditions for similar triangles?
- Two angles in one
triangle are equal to two angles in another
triangle.
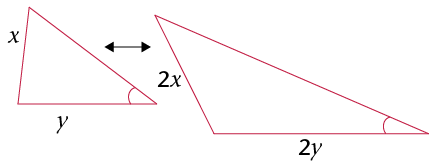
- Two sides of one
triangle are in the same proportion as two sides in
another triangle.
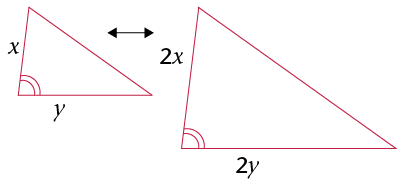
- Two sides of one
triangle are in the same proportion as two sides in
another triangle, and the angle between the two sides
is equal to the angle between the corresponding
sides.
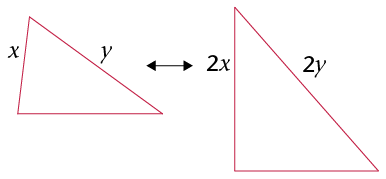
- Two sides of one
triangle are in the same proportion as two sides in
another triangle, and one angle not between the two
sides is equal to the corresponding angle in the other
triangle.
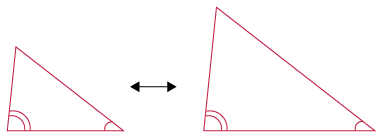
- Two angles in one
triangle are equal to two angles in another
triangle.
Parallel lines never meet. Two lines are parallel to each other if the distance between them is the same along the whole length of the lines.
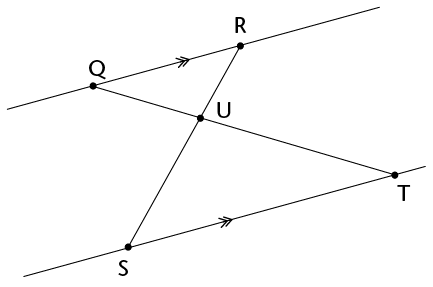
Complete the following proof that \(\triangle\)QRU \(|||\) \(\triangle\)TSU:
|
Statement |
Reason |
|
\(\text{R}\)\(\hat{\text{Q}}\)\(\text{T}\) = \(\text{Q}\)\(\hat{\text{T}}\)\(\text{S}\) \(\text{Q}\)\(\hat{\text{R}}\)\(\text{S}\)=
\(\therefore\)\(\triangle\)QRU\(|||\) \(\triangle\)TSU |
Alt. \(\angle\)s Vert. opp. \(\angle\)s Equal \(\angle\)s (or AAA) |
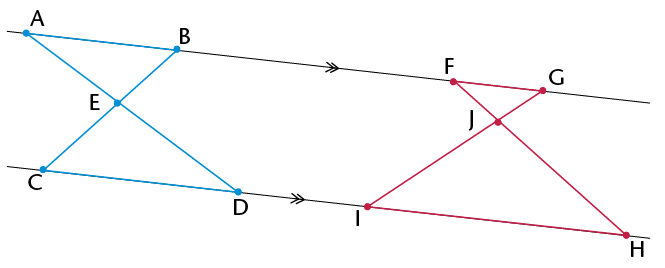
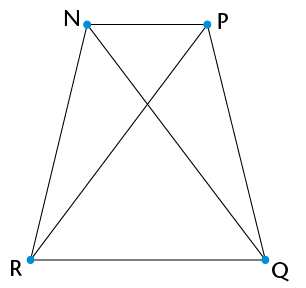
- Are the triangles in each pair similar?
Explain.
- Write down pairs of
similar triangles.
- Are triangles like these always similar?
Explain how you can be sure without measuring every possible
triangle pair.
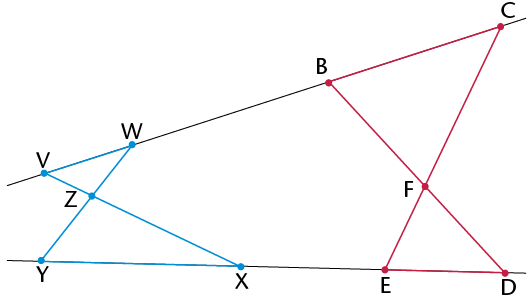
|
|
Statement |
Reason |
|
|
|
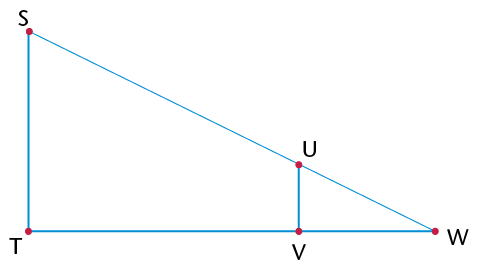
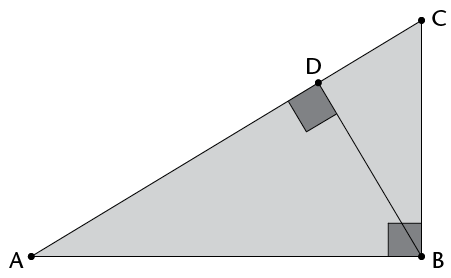
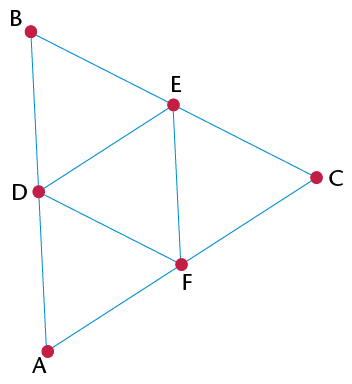
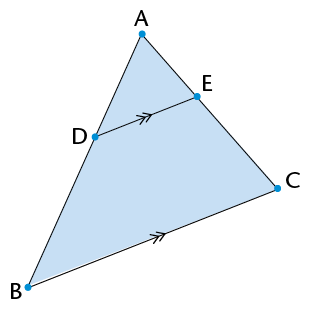
- Prove that \(\triangle\)BDE is an
equilateral triangle.
- Find all the congruent triangles. Give a
proof for each.
- Name as many similar triangles as you
can. Explain how you know they are similar.
- What is the proportion of the
corresponding sides of the similar triangles?
- Prove that DE is parallel to AC.
- Is DF parallel to BC? Is EF parallel to
BA? Explain.