17.4 Series resistors
|
Previous
17.3 Resistance
|
Next
17.5 Parallel resistors
|
17.4 Series resistors (ESAFJ)
When we add resistors in series to a circuit:
-
There is only one path for current to flow which ensures that the current is the same at every point in the circuit.
-
The voltage is divided across the resistors. The voltage across the battery in the circuit is equal to the sum of voltages across the series resistors:
\[{V}_{battery} = {V}_{1} + {V}_{2} + \ldots\] -
The resistance to the flow of current increases. The total resistance, \({R}_{S}\), is given by:
\[{R}_{S} = {R}_{1} + {R}_{2} + \ldots\]
We will revisit each of these features of series circuits in more detail below.
When resistors are in series, one after the other, there is a potential difference across each resistor. The total potential difference across a set of resistors in series is the sum of the potential differences across each of the resistors in the set.
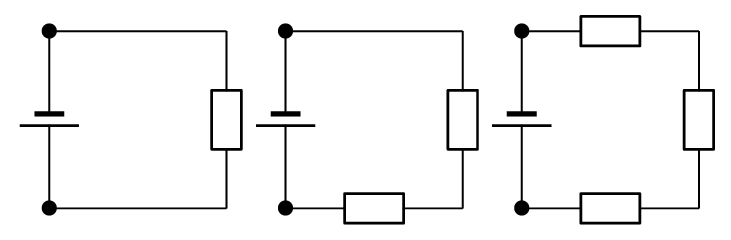
\[{V}_{battery} = {V}_{1} + {V}_{2} + \ldots\]Look at the circuits below. If we measured the potential difference between the black dots in all of these circuits it would be the same as we saw earlier. So we now know the total potential difference is the same across one, two or three resistors. We also know that some work is required to make charge flow through each resistor.
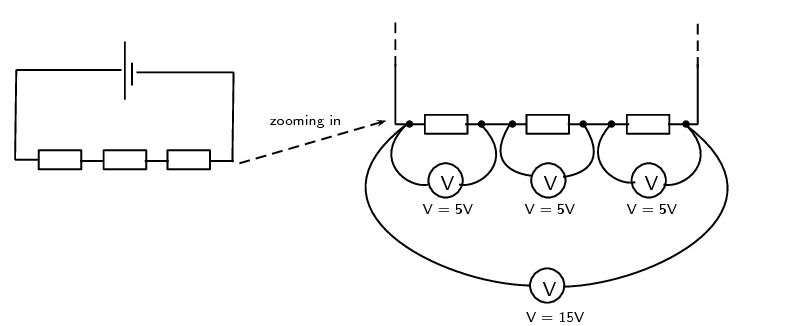
Let us look at this in a bit more detail. In the picture below you can see what the different measurements for 3 identical resistors in series could look like. The total voltage across all three resistors is the sum of the voltages across the individual resistors. Resistors in series are known as voltage dividers because the total voltage across all the resistors is divided amongst the individual resistors.
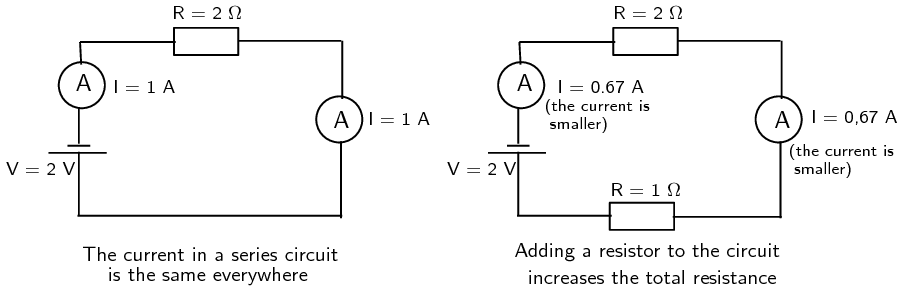
Consider the diagram below. On the left there is a circuit with a single resistor and a battery. No matter where we measure the current, it is the same in a series circuit. On the right, we have added a second resistor in series to the circuit. The total resistance of the circuit has increased and you can see from the reading on the ammeter that the current in the circuit has decreased.
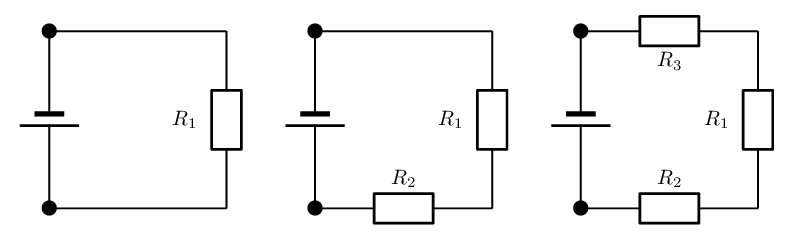
Voltage dividers
Aim
Test what happens to the current and the voltage in series circuits when additional resistors are added.
Apparatus
-
A battery
-
A voltmeter
-
An ammeter
-
Wires
-
Resistors
Method
-
Construct each circuit shown below
-
Measure the voltage across each resistor in the circuit.
-
Measure the current before and after each resistor in the circuit.
Results and conclusions
-
Compare the sum of the voltages across all the resistors in each of the circuits.
-
Compare the various current measurements within the same circuit.
The total resistance is equal to \({R}_{1}\) in the first circuit, to \({R}_{1} + {R}_{2}\) in the second circuit and \({R}_{1} + {R}_{2} + {R}_{3}\) in the third circuit. In general, for resistors in series, the total resistance is given by:
\[{R}_{S} = {R}_{1} + {R}_{2} + \ldots\]We know that the potential energy lost across a resistor is proportional to the resistance of the component because the higher the resistance the more work must be done to drive charge through the resistor.
Worked example 4: Series resistors I
A circuit contains two resistors in series. The resistors have resistance values of \(\text{5}\) \(\text{Ω}\) and \(\text{17}\) \(\text{Ω}\).

What is the total resistance in the circuit?
Analyse the question
We are told that the circuit is a series circuit and that we need to calculate the total resistance. The values of the two resistors have been given in the correct units, Ω.
Apply the relevant principles
The total resistance for resistors in series is the sum of the individual resistances. We can use
\[{R}_{S} = {R}_{1} + {R}_{2} + \ldots\]We have only two resistors and we now the resistances. In this case we have that:
\begin{align*} {R}_{S} & = {R}_{1} + {R}_{2} + \ldots \\ {R}_{S} & = {R}_{1} + {R}_{2} \\ & = \text{5}\text{ Ω} + \text{17}\text{ Ω} \\ & = \text{22}\text{ Ω} \end{align*}Quote the final result
The total resistance of the resistors in series is \(\text{22}\) \(\text{Ω}\)
Worked example 5: Series resistors II
A circuit contains three resistors in series. The resistors have resistance values of \(\text{0,5}\) \(\text{Ω}\), \(\text{7,5}\) \(\text{Ω}\) and \(\text{11}\) \(\text{Ω}\).
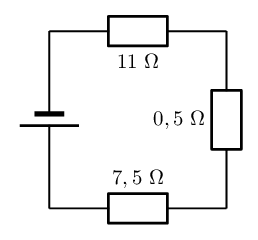
What is the total resistance in the circuit?
Analyse the question
We are told that the circuit is a series circuit and that we need to calculate the total resistance. The values of the three resistors have been given in the correct units, Ω.
Apply the relevant principles
The total resistance for resistors in series is the sum of the individual resistances. We can use
\[{R}_{S}={R}_{1}+{R}_{2}+ \ldots\]. We have three resistors and we now the resistances. In this case we have that:
\begin{align*} {R}_{S} & = {R}_{1} + {R}_{2} + \ldots \\ {R}_{S} & = {R}_{1} + {R}_{2} + {R}_{3} \\ & = \text{0,5}\text{ Ω} + \text{7,5}\text{ Ω} + \text{11}\text{ Ω} \\ & = \text{19}\text{ Ω} \end{align*}Quote the final result
The total resistance of the resistors in series is \(\text{19}\) \(\text{Ω}\)
Worked example 6: Series resistors III
A circuit contains two resistors in series. The resistors have resistance values of \(\text{750}\) \(\text{kΩ}\) and \(\text{1,7}\) \(\text{MΩ}\).
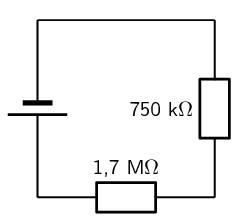
What is the total resistance in the circuit?
Analyse the question
We are told that the circuit is a series circuit and that we need to calculate the total resistance. The values of the two resistors have been given in the correct units, Ω.
Apply the relevant principles
The total resistance for resistors in series is the sum of the individual resistances. We can use
\[{R}_{S}={R}_{1}+{R}_{2}+ \ldots\]We have only two resistors and we know the resistances. In this case we have that:
\begin{align*} {R}_{S} & = {R}_{1} + {R}_{2} + \ldots \\ {R}_{S} & = {R}_{1} + {R}_{2} \\ & = \text{750}\text{ kΩ} + \text{1,7}\text{ MΩ} \\ & = \text{750} \times \text{10}^{\text{3}}\text{ Ω} + \text{1,7} \times \text{10}^{\text{6}}\text{ Ω} \\ & = \text{0,75} \times \text{10}^{\text{6}}\text{ Ω} + \text{1,7} \times \text{10}^{\text{6}}\text{ MΩ} \\ & = \text{2,45} \times \text{10}^{\text{6}}\text{ Ω} \\ & = \text{2,45}\text{ MΩ} \end{align*}Quote the final result
The total resistance of the resistors in series is \(\text{2,45}\) \(\text{MΩ}\).
|
Previous
17.3 Resistance
|
Table of Contents |
Next
17.5 Parallel resistors
|
