11.2 Wave-like nature of EM radiation
|
Previous
11.1 What is electromagnetic radiation?
|
Next
11.3 Electromagnetic spectrum
|
11.2 Wave-like nature of EM radiation (ESADI)
If you watch a colony of ants walking up the wall, they look like a thin continuous black line. But as you look closer, you see that the line is made up of thousands of separated black ants.
Light and all other types of electromagnetic radiation seem like a continuous wave at first, but when one performs experiments with light, one can notice that light can have both wave- and particle-like properties. Just like the individual ants, light can also be made up of individual bundles of energy, or quanta of light.
Light has both wave-like and particle-like properties (wave–particle duality), but only shows one or the other, depending on the kind of experiment we perform. A wave-type experiment shows the wave nature, and a particle-type experiment shows particle nature. One cannot test the wave and the particle nature at the same time. A particle of light is called a photon.
- Photon
-
A photon is a quantum (energy packet) of light.
Fields (ESADJ)
Accelerating charges emit electromagnetic waves. A changing electric field generates a magnetic field and a changing magnetic field generates an electric field. This is the principle behind the propagation of electromagnetic waves, because electromagnetic waves, unlike sound waves, do not need a medium to travel through.
EM waves propagate when an electric field oscillating in one plane produces a magnetic field oscillating in a plane at right angles to it, which produces an oscillating electric field, and so on. The propagation of electromagnetic waves can be described as mutual induction. The changing electric field is responsible for inducing the magnetic field and vice versa.
We use E to denote electric fields and B to denote magnetic fields.
These concepts will be covered in more detail in Grade 11.
These mutually regenerating fields, most commonly described as self-propagating, travel through empty space at a constant speed of approximately \(\text{3} \times \text{10}^{\text{8}}\) \(\text{m·s$^{-1}$}\), represented by c. We will use \(\text{3} \times \text{10}^{\text{8}}\) \(\text{m·s$^{-1}$}\) for all of our calculations in this book. Although an electromagnetic wave can travel through empty space, it can also travel through a medium (such as water and air). When an electromagnetic wave travels through a medium, it travels slower than it would through empty space (vacuum).
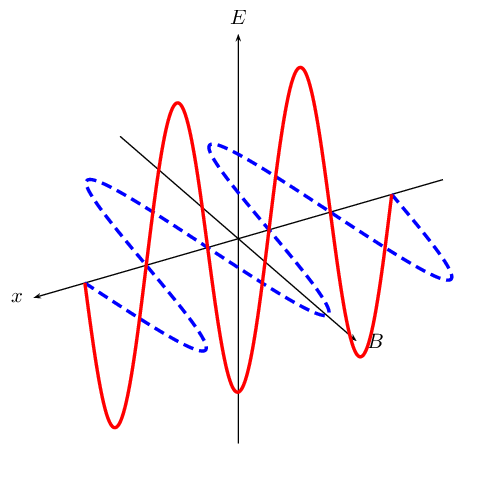
Figure 11.1: A diagram showing the mutually regenerating electric field (red (solid) line) and magnetic field (blue (dashed) line).
Since an EM radiation is a wave, the following equation still applies:
\[v = f \cdot \lambda\]Except that we can replace \(v\) with \(c\):
\[c = f \cdot \lambda\]Worked example 1: EM radiation I
Calculate the frequency of an electromagnetic wave with a wavelength of \(\text{4,2} \times \text{10}^{-\text{7}}\) \(\text{m}\).
Wave equation
We use the formula: \(c = f \cdot \lambda\) to calculate frequency. The speed of light is a constant \(\text{3} \times \text{10}^{\text{8}}\) \(\text{m·s$^{-1}$}\).
Calculate
\begin{align*} c & = f\lambda \\ \text{3} \times \text{10}^{\text{8}}\text{ m·s$^{-1}$} & = f \times \text{4,2} \times \text{10}^{-\text{7}}\text{ m} \\ f & = \text{7,14} \times \text{10}^{\text{14}}\text{ Hz} \end{align*}Quote the final answer
The frequency is \(\text{7} \times \text{10}^{\text{14}}\) \(\text{Hz}\).
Worked example 2: EM Radiation II
An electromagnetic wave has a wavelength of \(\text{200}\) \(\text{nm}\). What is the frequency of the radiation?
What do we know?
Recall that all radiation travels at the speed of light (\(c\)) in vacuum. Since the question does not specify through what type of material the wave is travelling, one can assume that it is travelling through a vacuum. We can identify two properties of the radiation - wavelength (\(\text{200}\) \(\text{nm}\)) speed (\(c\)).
Apply the wave equation
\begin{align*} c & = f\lambda \\ \text{3} \times \text{10}^{\text{8}}\text{ m·s$^{-1}$} & = f \times \text{200} \times \text{10}^{-\text{9}}\text{ m} \\ f & = \text{1,5} \times \text{10}^{\text{15}}\text{ Hz} \end{align*}Quote the final answer
The frequency is \(\text{1,5} \times \text{10}^{\text{15}}\) \(\text{Hz}\).
|
Previous
11.1 What is electromagnetic radiation?
|
Table of Contents |
Next
11.3 Electromagnetic spectrum
|
