Calculate the electric field strength \(\text{20}\) \(\text{m}\) from a \(\text{7}\) \(\text{nC}\)
charge.
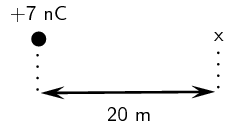
We need to calculate the electric field a distance from a given charge. We are given the magnitude of the
charge and the distance from the charge. We will use the equation:
\(E=k\frac{Q}{{r}^{2}}.\)
\begin{align*}
E & = \frac{kQ}{r^2} \\
& = \frac{(\text{9,0} \times \text{10}^{\text{9}})(\text{7} \times
\text{10}^{-\text{9}})}{\text{20}^2} \\
& = \text{0,15}\text{ N·C$^{-1}$}
\end{align*}
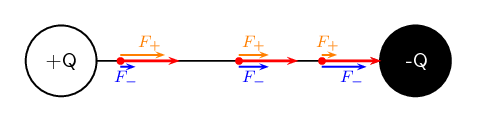
Two charges of \({Q}_{1}=-\text{6}\text{ pC}\) and \({Q}_{2}=-\text{8}\text{ pC}\) are separated by a
distance of \(\text{3}\) \(\text{km}\). What is the electric field strength at a point that is
\(\text{2}\) \(\text{km}\) from \({Q}_{1}\) and \(\text{1}\) \(\text{km}\) from \({Q}_{2}\)? The point
lies between \({Q}_{1}\) and \({Q}_{2}\).

We need to calculate the electric field a distance from two given charges. We are given the magnitude of
the charges and the distances from the charges.
We will use the equation:
\(E=k\frac{Q}{{r}^{2}}.\)
We need to calculate the electric field for each charge separately and then add them to determine the
resultant field.
We first solve for \({Q}_{1}\):
\begin{align*}
E &= \frac{kQ}{r^2} \\
&= \frac{(\text{9,0} \times \text{10}^{\text{9}})(\text{6} \times \text{10}^{-\text{12}})}{(\text{2}
\times \text{10}^{\text{3}})^2} \\
& = \text{1,3} \times \text{10}^{-\text{8}}\text{ N·C$^{-1}$}
\end{align*}
Then for \({Q}_{2}\):
\begin{align*}
E &= \frac{kQ}{r^2} \\
&= \frac{(\text{9,0} \times \text{10}^{\text{9}})(\text{8} \times \text{10}^{-\text{12}})}{(\text{1}
\times \text{10}^{\text{3}})^2} \\
& = \text{7,1} \times \text{10}^{-\text{8}}\text{ N·C$^{-1}$}
\end{align*}
We need to subtract the two electric fields because they are in opposite directions. The electric fields
due to each charge will be towards the charge causing it.
Therefore, \({E}_{\text{total}}= \text{1,3} \times \text{10}^{-\text{8}} - \text{7,1} \times
\text{10}^{-\text{8}} = -\text{5,8} \times \text{10}^{-\text{8}}\text{ N·C$^{-1}$}\) in the direction
of the \(-\text{8}\) \(\text{pC}\) charge.