11.3 Alternating current | Electrodynamics

11.2 Electrical machines - generators and motors

11.3 Alternating current (ESCQC)

Most students learning about electricity begin with what is known as direct current (DC), which is electricity flowing in one direction only. DC is the kind of electricity made by a battery, with definite positive and negative terminals.

However, we have seen that the electricity produced by some generators constantly alternates (switches direction) and is therefore known as alternating current (AC). There are a number of advantages to AC current, the main advantage to AC is that the voltage can be changed using transformers. That means that the voltage can be "stepped up" at power stations to a very high voltage so that electrical energy can be transmitted along power lines at low current and therefore experience low energy loss due to heating. The voltage can then be stepped down for use in buildings and street lights.

A list of the advantages of AC current:

Easy to be transformed (step up or step down using a transformer).
Easier to convert from AC to DC than from DC to AC.
Easier to generate.
It can be transmitted at high voltage and low current over long distances with less energy lost.
High frequency used in AC makes it suitable for motors.

In South Africa alternating current is generated at a frequency of \(\text{50}\) \(\text{Hz}\).

The circuit symbol for alternating current is:

temp text

Current and voltage (ESCQD)

In an ideal DC circuit, current and voltage are constant. In an AC circuit, current and voltage vary with time. The value of the current or voltage at any specific time is called the instantaneous current or voltage and is calculated as follows:

\begin{align*} %i& = {I}_{\max}\sin\left(\text{2}\pi ft \right)\\ % v& = {V}_{\max}\sin\left(\text{2}\pi ft\right) \\ i& = {I}_{\max}\sin\left(\omega t \right)\\ v& = {V}_{\max}\sin\left(\omega t\right) \end{align*}

\(i\) is the instantaneous current. \({I}_{\max}\) is the maximum current. \(v\) is the instantaneous voltage. \({V}_{\max}\) is the maximum voltage. \(f\) is the frequency of the AC and t is the time at which the instantaneous current or voltage is being calculated.

The value we use for AC is known as the root mean square (rms) average. This is the same as what the DC voltage would be for the same source and is defined as:

\begin{align*} {I}_{rms}& = \frac{{I}_{\max}}{\sqrt{\text{2}}}\\ {V}_{rms}& = \frac{{V}_{\max}}{\sqrt{\text{2}}} \end{align*}

Since AC varies sinusoidally, with as much positive as negative, doing a straight average would get you zero for the average voltage. The rms value by-passes this problem.

temp text

Worked example 1: Laptop transformer

The transformer for the laptop on which this book was written has the following information:

INPUT: \(\text{100}\)-\(\text{240}\) \(\text{V}\); \(\text{1,5}\) \(\text{A}\); \(\text{50}\)/\(\text{60}\) \(\text{Hz}\)
OUTPUT: \(\text{20}\) \(\text{V}\); \(\text{3,25}\) \(\text{A}\)

What changes from input to output, apart from the voltage and current values, and what does that imply? In addition, calculate the maximum current and voltage values for the input and/or output as appropriate.

Comparing input and output

The input description includes a frequency because it is designed for regular household use where we use alternating current. The output doesn't include a frequency. This implies that the output is not alternating current. This means that the output voltage and current will be constant with time.

Maximum values

When dealing with alternating current, the value given on electrical appliances is the root mean square (rms) value. The transformer takes alternating current input and produces direct current output, this means that we only need to determine the maximum values for the input.

\begin{align*} V_{\text{rms}} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \text{240}\text{ V} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore V_{\text{max}} &= \text{339,41125}\ldots\text{ V} \end{align*}

Therefore \(V_{\text{max}}\approx\text{339,41}\text{ V}\)

\begin{align*} I_{\text{rms}} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \text{1,5 A} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore I_{\text{max}}& = \text{2,1213}\ldots\text{ A} \end{align*}

Therefore \(I_{\text{max}}\approx\text{2,12}\text{ A}\)

Worked example 2: Camera battery charger

A camera charger has the following information:

INPUT: \(\text{100}\)-\(\text{240}\) \(\text{V}\); \(\text{0,085}\) \(\text{A}\) (\(\text{100}\) \(\text{V}\)) - \(\text{0,05}\) \(\text{A}\) (\(\text{240}\) \(\text{V}\)) ; \(\text{50}\)/\(\text{60}\) \(\text{Hz}\)
OUTPUT: \(\text{4,2}\) \(\text{V}\); \(\text{0,7}\) \(\text{A}\)

Calculate the maximum current and voltage values for both \(\text{100}\) \(\text{V}\) and \(\text{240}\) \(\text{V}\) input.

Understanding the two cases

The reason the transformer has the different input voltages listed is because it may be used internationally and not all countries use the same household voltage. The transformers purpose is to ensure that the output is consistent regardless of the input voltage. The different input voltages of \(\text{100}\) \(\text{V}\) and \(\text{240}\) \(\text{V}\) result in different input current values. This is why two different current values are listed under input but the voltage in parentheses tells you which case they are applicable to.

The cases are:

\(\text{100}\) \(\text{V}\): \(\text{0,085}\) \(\text{A}\)
\(\text{240}\) \(\text{V}\): \(\text{0,05}\) \(\text{A}\)

Input voltage of \(\text{100}\) \(\text{V}\)

\begin{align*} V_{\text{rms}} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \text{100}\text{ V} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore V_{\text{max}} & = \text{141,42135}\ldots\text{ V} \end{align*}

Therefore \(V_{\text{max}}\approx\text{141,42}\text{ V}\)

\begin{align*} I_{\text{rms}} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \text{0,085}\text{ A} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore I_{\text{max}} & = \text{0,12020}\ldots\text{ A} \end{align*}

Therefore \(I_{\text{max}}\approx\text{0,12}\text{ A}\)

Input voltage of \(\text{240}\) \(\text{V}\)

\begin{align*} V_{\text{rms}} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \text{240 V} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore V_{\text{max}}& = \text{339,41125}\ldots\text{ V} \end{align*}

Therefore \(V_{\text{max}}\approx\text{339,41}\text{ V}\)

\begin{align*} I_{\text{rms}} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \text{0,5 A} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \\ \therefore I_{\text{max}}& = \text{0,70710}\ldots\text{ A} \end{align*}

Therefore \(I_{\text{max}}\approx\text{0,71}\text{ A}\)

Alternating current

Textbook Exercise 11.2

Explain the advantages of alternating current.

Easy to be transformed (step up or step down using a transformer).
Easier to convert from AC to DC than from DC to AC.
Easier to generate.
It can be transmitted at high voltage and low current over long distances with less energy lost.
High frequency used in AC makes it suitable for motors.

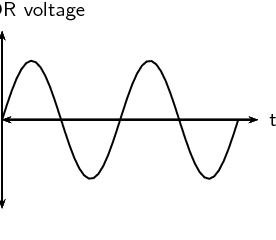
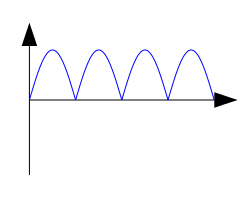
Which of the following graphs correctly shows the current vs. time graph for an AC generator?


A	B

C	D

For an alternating current generator, the current vs. time graph is a sine wave and alternates between positive and negative values.

For a direct current generator, the current vs. time graph is the absolute value of a sine wave and does not alternate between positive and negative values.

The correct answer is C.

Write expressions for the current and voltage in an AC circuit.

\begin{align*} i & = I_{\max}\sin(\text{2}πft+φ)\\ v & = V_{\max}\sin(\text{2}πft) \end{align*}

Define the rms (root mean square) values for current and voltage for AC.

The root mean square is the value that we use for AC and is what it's DC equivalent would be.

\begin{align*} I_{rms} & =\frac{I_{\max}}{\sqrt{\text{2}}}\\ V_{rms} & =\frac{V_{\max}}{\sqrt{\text{2}}} \end{align*}

What is the frequency of the AC generated in South Africa?

In South Africa the frequency is \(\text{50}\) \(\text{Hz}\)

If \({V}_{\mathrm{\max}}\) at a power station generator is \(\text{340}\) \(\text{V}\) AC, what is the mains supply (rms voltage) in our household?

\begin{align*} V_{rms} & = \frac{V_{\max}}{\sqrt{\text{2}}} \\ & = \frac{\text{340}}{\sqrt{\text{2}}}\\ & = \text{240,42}\text{ V} \end{align*}

Given: \(I_{\text{max}}\) is \(\text{10}\) \(\text{A}\)

Calculate the rms (root mean square) current to two decimal places.

\begin{align*} I_{\text{rms}} & = \frac{I_{\text{max}}}{\sqrt{\text{2}}} \end{align*}\begin{align*} I_{\text{rms}} & = \frac{\text{10}\text{ A}}{\sqrt{\text{2}}} \\ & = \text{7,07}\text{ A} \end{align*}

Therefore \(I_{\text{rms}}=\text{7,07}\text{ A}\)

\(\text{7,07}\)

Given: \(V_{\text{max}}\) is \(\text{266}\) \(\text{V}\)

Calculate the rms (root mean square) voltage to two decimal places.

\begin{align*} V_{\text{rms}} & = \frac{V_{\text{max}}}{\sqrt{\text{2}}} \end{align*}\begin{align*} V_{\text{rms}} & = \frac{\text{266}\text{ V}}{\sqrt{\text{2}}} \\ & = \text{188,09}\text{ V} \end{align*}

Therefore \(V_{\text{rms}}=\text{188,09}\text{ V}\)

\(\text{188,09}\) \(\text{V}\)

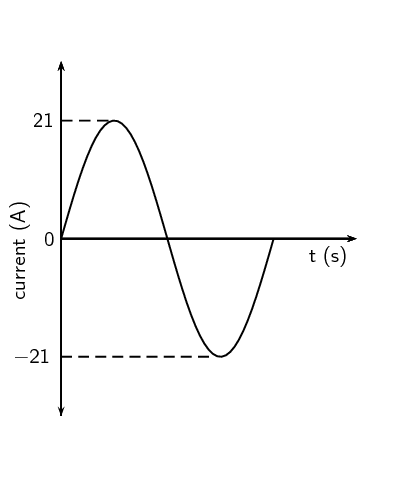
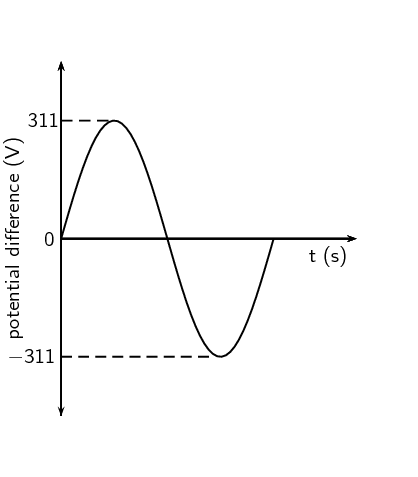
Draw a graph of voltage vs time and current vs time for an AC circuit.

The graph is the same for both voltage and for current:

Power (ESCQF)

If the current and voltage are functions of time, so they are always changing, then so will the power that is dissipated in any circuit element. In circuits which contain only ohmic resistors the average power dissipated in any component can be calculated in terms of the rms values.

\begin{align*} P_{av} &=I_{rms}V_{rms} \\ &=\frac{I_{\max}}{\sqrt{\text{2}}}\frac{V_{\max}}{\sqrt{\text{2}}}\\ &=\frac{\text{1}}{\text{2}}I_{\max}V_{\max} \end{align*}

You might ask why we don't need to use an rms value for power. In an AC circuit both the current and voltage have the same sign so they are both either positive or negative. This means that power, the product of the two is always positive. If power is always positive then the average value won't be zero as in the case of current or voltage in AC circuits.

Worked example 3: Laptop transformer power

The transformer for a laptop has the following information:

INPUT: \(\text{100}\)-\(\text{240}\) \(\text{V}\); \(\text{1,5}\) \(\text{A}\); \(\text{50}\)/\(\text{60}\) \(\text{Hz}\)
OUTPUT: \(\text{20}\) \(\text{V}\); \(\text{3,25}\) \(\text{A}\)

Using the input values and assuming \(\text{240}\) \(\text{V}\), what is the average power dissipated in the transformer?

Calculate the average power

The values given on electrical appliance labels are the root mean square (rms) values. We use those to calculate the average power.

\begin{align*} P_{avg} &=I_{rms}V_{rms} \\ &= \text{1,5}\text{ A} \cdot \text{240}\text{ V}\\ & = \text{360}\text{ W} \end{align*}

Worked example 4: Motors and generators [NSC 2011 Paper 1]

Diesel-electric trains make use of electric motors as well as generators.

The table below compares a motor and a generator in terms of the type of energy conversion and the underlying principle on which each operates. Complete the table by writing down only the question number (11.1.1–11.1.4) in the ANSWER BOOK and next to each number the answer.

	TYPE OF ENERGY CONVERSION	PRINCIPLE OF OPERATION
Motor	11.1.1	11.1.3
Generator	11.1.2	11.1.4

(4 marks)

The simplified diagram below represents an electric motor.

Give a reason why the section of the coil labelled BC in the above diagram does not experience a magnetic force whilst the coil is in the position as shown.

(2 marks)
Graphs of the current and potential difference outputs of an AC generator are shown below.

Calculate the average power output of this generator.

(6 marks)

[TOTAL: 12 marks]

Electrical (energy) to mechanical (kinetic) energy
Mechanical (kinetic) energy to electrical (energy)
Motor effect
Electromagnetic induction

(4 marks)

Question 2

BC (conductor) is parallel to the magnetic field.

Open switch, no current

(2 marks)

Question 3

Option 1:

\begin{align*} P_{\text{ave}} &= V_{\text{rms}} I_{\text{rms}} \\ &= \frac{V_{\text{max}}}{\sqrt{2}} \cdot \frac{I_{\text{max}}}{\sqrt{2}} \\ &= \frac{(311)(21)}{2} \\ &= \text{3265,5 W} \end{align*}

\begin{align*} P_{\text{max}} &= V_{\text{max}}I_{\text{max}} \\ & = (311)(21) \\ & = \text{6531 W} \\ \therefore P_{\text{ave}} & = \frac{P_{\text{max}}}{2} \\ & = \frac{\text{6 531}}{2} \\ & = \text{3265,5 W} \end{align*}

Option 2:

\begin{align*} V_{\text{rms}} &= \frac{V_{\text{max}}}{\sqrt{2}} \\ &= \frac{311}{\sqrt{2}} \\ &= \text{219,91}\text{ V} \end{align*}\begin{align*} I_{\text{rms}} &= \frac{I_{\text{max}}}{\sqrt{2}} \\ &= \frac{21}{\sqrt{2}} \\ &= \text{14,85}\text{ A} \end{align*}\begin{align*} P_{\text{ave}} & =V_{\text{rms}}I_{\text{rms}}\\ & =(\text{219,91})(\text{14,85})\\ & = \text{3 265,66}\text{ W} \end{align*}

Option 3:

\begin{align*} R & = \frac{V}{I} \\ & = \frac{\text{311}}{\text{21}}\\ & = \text{14,81}\ \Omega \end{align*}\begin{align*} I_{\text{rms}} &= \frac{I_{\text{max}}}{\sqrt{2}} \\ &= \frac{21}{\sqrt{2}} \\ &= \text{14,85}\text{ A} \end{align*}\begin{align*} P_{\text{ave}} &= I_{\text{rms}}^{2}R \\ &= (\text{14,85})^{2}(\text{14,81}) \\ &= \text{3 265,83}\text{ W} \end{align*}

Option 4:

\begin{align*} R & = \frac{V}{I} \\ & = \frac{\text{311}}{\text{21}}\\ & = \text{14,81}\ \Omega \end{align*}\begin{align*} V_{\text{rms}} &= \frac{V_{\text{max}}}{\sqrt{2}} \\ &= \frac{311}{\sqrt{2}} \\ &= \text{219,91}\text{ V} \end{align*}\begin{align*} P_{\text{ave}} &= \frac{V_{\text{rms}}^{2}}{R} \\ &= \frac{(\text{219,41})^2}{(\text{14,81})} \\ &= \text{3 265,83}\text{ W} \end{align*}

(6 marks)

[TOTAL: 12 marks]

temp text

11.2 Electrical machines - generators and motors

Table of Contents

11.4 Chapter summary