Momentum is a physical quantity which is closely related to forces. Momentum is
a property which applies to moving objects, in fact it is mass in motion. If something
has mass and it is moving then it has momentum.
The momentum (symbol \(\vec{p}\)) of an object of mass \(m\)
moving at velocity \(v\) is:
\[\vec{p}=m\vec{v}\]
Momentum is directly proportional to both the mass and velocity of an object. A small car
travelling at the same velocity as a big truck will have a smaller momentum than
the truck. The smaller the mass, the smaller the momentum for a fixed velocity. If
the mass is constant then the greater the velocity the greater the momentum. The momentum
will always be in the same direction as the velocity because mass is a scalar not a
vector.
Vector nature of momentum (ESCJ8)
A car travelling at \(\text{120}\) \(\text{km·hr$^{-1}$}\) will have a larger momentum
than the same car travelling at \(\text{60}\) \(\text{km·hr$^{-1}$}\). Momentum is
also related to velocity; the smaller the velocity, the smaller the momentum.
Different objects can also have the same momentum, for example a car travelling slowly can
have the same momentum as a motorcycle travelling relatively fast. We can easily
demonstrate this.
Consider a car of mass \(\text{1 000}\) \(\text{kg}\)
with a velocity of \(\text{8}\) \(\text{m·s$^{-1}$}\)
(about \(\text{30}\) \(\text{km·hr$^{-1}$}\)) East.
The momentum of the car is therefore:
\begin{align*}
\vec{p}& = m\vec{v} \\
& = \left(\text{1 000}\right)\left(8\right) \\
& = \text{8 000}\text{ kg·m·s$^{-1}$}~\text{East}
\end{align*}
Now consider a motorcycle, also travelling East, of mass
\(\text{250}\) \(\text{kg}\)
travelling at \(\text{32}\) \(\text{m·s$^{-1}$}\)
(about \(\text{115}\) \(\text{km·hr$^{-1}$}\)).
The momentum of the motorcycle is:
\begin{align*}
\vec{p} &= m\vec{v} \\
& = \left(250 \text{kg}\right)\left(32 \text{m·s$^{-1}$}\right) \\
& = \text{8 000}\text{ kg·m·s$^{-1}$}~\text{East}
\end{align*}
Even though the motorcycle is considerably lighter than the car, the fact that the motorcycle
is travelling much faster than the car means that the momentum of both vehicles is the
same.
From the calculations above, you are able to derive the unit for momentum as
\(\text{kg·m·s$^{-1}$}\).
Momentum is also vector quantity, because it is the product of a scalar (\(m\)) with a
vector \((\vec{v})\).
A vector multiplied by a scalar has the same direction as the original vector but a
magnitude that is scaled by the multiplicative
factor.
This means that whenever we calculate the momentum of an object, we should include
the direction of the momentum.
Worked example 1: Momentum of a soccer ball
A soccer ball of mass \(\text{420}\) \(\text{g}\)
is kicked at \(\text{20}\) \(\text{m·s$^{-1}$}\)
towards the goal post. Calculate the momentum of the ball.

Identify what information is given and what is asked for
The question explicitly gives:
The mass of the ball must be converted to SI units.
\(\text{420}\text{ g}=\text{0,42}\text{ kg}\)
We are asked to calculate the momentum of the ball. From the definition of
momentum,
\(\vec{p}=m\vec{v}\) we see that we need the mass and velocity of the
ball, which we are given.
Do the calculation
We calculate the magnitude of the momentum of the ball,
\begin{align*}
\vec{p}& = m\vec{v} \\
& = \left(\text{0,42}\right)\left(20\right) \\
& = \text{8,40}\text{ kg·m·s$^{-1}$}
\end{align*}
Quote the final answer
We quote the answer with the direction of motion included,
\(\vec{p}\) = \(\text{8,40}\) \(\text{kg·m·s$^{-1}$}\) in the
direction of the goal post.
Worked example 2: Momentum of a cricket ball
A cricket ball of mass \(\text{160}\) \(\text{g}\) is bowled at \(\text{40}\)
\(\text{m·s$^{-1}$}\) towards a batsman. Calculate the momentum of
the cricket ball.

Identify what information is given and what is asked for
The question explicitly gives
-
the mass of the ball (m = \(\text{160}\) \(\text{g}\) =
\(\text{0,16}\) \(\text{kg}\)), and
-
the velocity of the ball \((\vec{v}\) = \(\text{40}\)
\(\text{m·s$^{-1}$}\) towards the batsman)
To calculate the momentum we will use
\(\vec{p}=m\vec{v}.\)
Do the calculation
\begin{align*}
\vec{p}& = m\vec{v} \\
& = \left(\text{0,16}\right)\left(40\right) \\
& = \text{6,4}\text{ kg·m·s$^{-1}$} \\
& = \text{6,4}\text{ kg·m·s$^{-1}$} \text{in the direction of
the batsman}
\end{align*}
Quote the final answer
The momentum of the cricket ball is \(\text{6,4}\)
\(\text{kg·m·s$^{-1}$}\) in the direction of the batsman.
Worked example 3: Momentum of the Moon
The centre of the Moon is approximately \(\text{384 400}\) \(\text{km}\)
away
from the centre of the Earth and orbits the Earth in \(\text{27,3}\)
days. If the Moon has a mass
of \(\text{7,35} \times \text{10}^{\text{22}}\) \(\text{kg}\), what is
the magnitude of its momentum (using the definition given in this
chapter) if we assume a circular orbit?
The actual momentum of the Moon is more complex but we do not cover that
in this chapter.

Identify what information is given and what is asked for
The question explicitly gives
-
the mass of the Moon (\(m\) = \(\text{7,35} \times
\text{10}^{\text{22}}\) \(\text{kg}\))
-
the distance to the Moon (\(\text{384 400}\)
\(\text{km}\) = \(\text{384 400 000}\)
\(\text{m}\) = \(\text{3,844} \times
\text{10}^{\text{8}}\) \(\text{m}\))
-
the time for one orbit of the Moon (\(\text{27,3} \text{
days} = \text{27,3} \times 24 \times 60 \times 60 =
\text{2,36} \times \text{10}^{\text{6}}\text{ s}\))
We are asked to calculate only the magnitude of the momentum of the Moon
(i.e. we do not need to specify a direction). In order to do this we
require the mass and the magnitude of the velocity of the Moon, since
\(\vec{p}=m\vec{v}.\)
Find the magnitude of the velocity of the Moon
The magnitude of the average velocity is the same as the speed. Therefore:
\(v=\frac{\Delta x}{\Delta t}\)
We are given the time the Moon takes for one orbit but not how far it travels
in that time. However, we can work this out from the distance to the
Moon and the fact that the Moon has a circular orbit. Using the equation
for the circumference, C, of a circle in terms of its radius, we can
determine the distance travelled by the Moon in one
orbit:
\begin{align*}
C& = 2\pi r \\
& = 2\pi \left(\text{3,844} \times \text{10}^{\text{8}}\right) \\
& = \text{2,42} \times \text{10}^{\text{9}}\text{ m}
\end{align*}
Combining the distance travelled by the Moon in an orbit and the time
taken by the Moon to complete one orbit, we can determine the
magnitude of the Moon's velocity or speed,
\begin{align*}
v& = \frac{\Delta x}{\Delta t} \\
& = \frac{C}{T} \\
& = \frac{\text{2,42} \times \text{10}^{\text{9}}\text{ m}}{\text{2,36}
\times \text{10}^{\text{6}}\text{ s}} \\
& = \text{1,02} \times \text{10}^{\text{3}}\text{ m·s$^{-1}$}
\end{align*}
Finally calculate the momentum and quote the answer
The magnitude of the Moon's momentum is:
\begin{align*}
\vec{p}& = m\vec{v} \\
{p}& = m{v} \\
& = \left(\text{7,35} \times \text{10}^{\text{22}}\right)\left(\text{1,02}
\times \text{10}^{\text{3}}\right) \\
& = \text{7,50} \times \text{10}^{\text{25}}\text{ kg·m·s$^{-1}$}
\end{align*}
The magnitude of the momentum of the Moon is \(\text{7,50} \times
\text{10}^{\text{25}}\) \(\text{kg·m·s$^{-1}$}\).
As we have said, momentum is a vector quantity. Since momentum is a vector, the techniques of
vector addition discussed in Vectors and scalars in Grade
10 must be used when dealing with momentum.
Change in momentum (ESCJ9)
Particles or objects can collide with other particles or objects, we know
that this will
often change their velocity (and maybe their mass) so their momentum is likely
to change as well. We will deal with collisions in detail a little bit later
but we are going to start by looking at the details of the change in momentum
for a single particle or object.
Case 1: Object bouncing off a wall
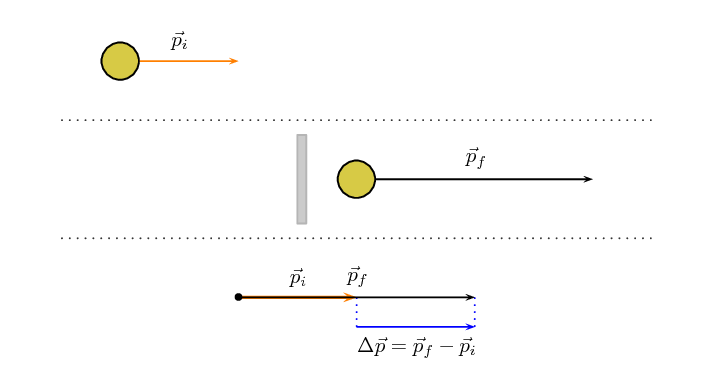
Lets start with a simple picture, a ball of mass, \(m\), moving
with initial velocity, \(\vec{v}_i\), to the right towards a wall.
It will have momentum
\(\vec{p}_i=m\vec{v}_i\) to the right as shown in this picture:

The ball bounces off the wall. It will now be moving to the left, with the same mass,
but a different velocity, \(\vec{v}_f\) and therefore, a different
momentum, \(\vec{p}_f=m\vec{v}_f\), as shown in this picture:
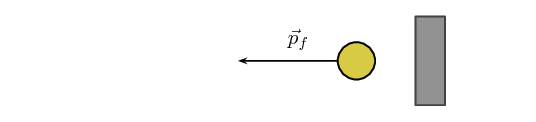
We know that the final momentum vector must be the sum of the initial momentum
vector and the change in momentum vector, \(\Delta \vec{p}=m\Delta \vec{v}\).
This means that, using tail-to-head vector addition, \(\Delta \vec{p}\), must
be the vector that starts at the head of \(\vec{p}_i\) and ends on the head of
\(\vec{p}_f\) as shown in this picture:

We also know from algebraic addition of vectors that:
\begin{align*}
\vec{p}_f &=\vec{p}_i + \Delta \vec{p} \\
\vec{p}_f - \vec{p}_i &= \Delta \vec{p} \\
\Delta \vec{p} &= \vec{p}_f - \vec{p}_i
\end{align*}
If we put this all together we can show the sequence and the change in momentum
in one diagram:
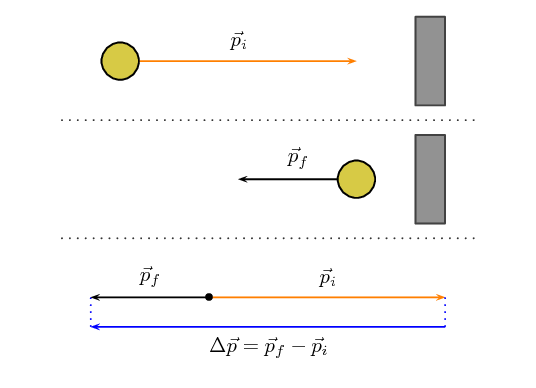
We have just shown the case for a rebounding object. There are a few other cases we
can use to illustrate the basic features but they are all built up in the same
way.
Case 2: Object stops

In some scenarios the object may come to a standstill (rest). An example of such a
case
is a tennis ball hitting the net. The net stops the ball but doesn't cause it to
bounce back.
At the instant before it falls to the ground its velocity is zero. This scenario
is described
in this image:
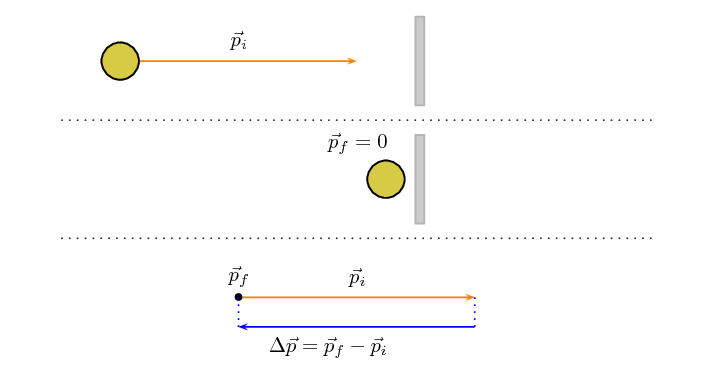
Case 3: Object continues more slowly
In this case, the object continue in the same direction but more slowly. To give this
some context, this could happen when a ball hits a glass window and goes through
it or an object sliding on a frictionless surface encounters a small rough patch
before carrying
on along the frictionless surface.
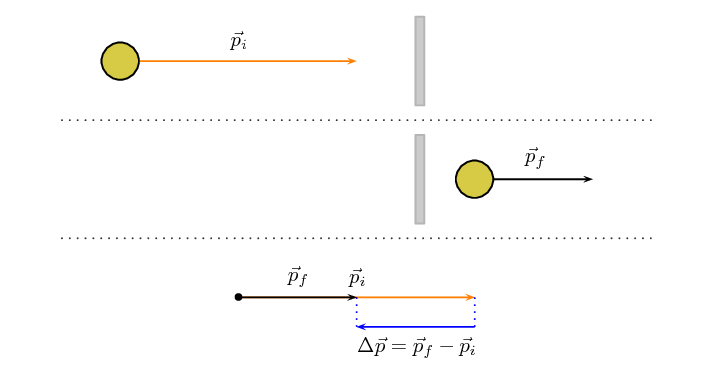
Important: note that even though the momentum remains in the same
direction the change in momentum is in the opposite direction because the
magnitude of the final momentum is less than the magnitude of the initial
momentum.
Case 4: Object gets a boost
In this case the object interacts with something that increases the velocity it has
without changing its direction. For example, in squash the ball can bounce off a
back wall
towards the front wall and a player can hit it with a racquet in the same
direction, increasing
its velocity.

If we analyse this scenario in the same way as the first 3 cases, it will look like
this:
Case 5: Vertical bounce
For this explanation we are ignoring any effect of gravity. This isn't
accurate but
we will learn more about the role of gravity in this scenarion in the
next chapter.
All of the examples that we've shown so far have been in the horizontal direction.
That is just a coincidence, this approach applies for vertical or horizontal
cases. In
fact, it applies to any scenario where the initial and final vectors fall on the
same
line, any 1-dimensional (1D) problem. We will only deal with 1D scenarios in
this
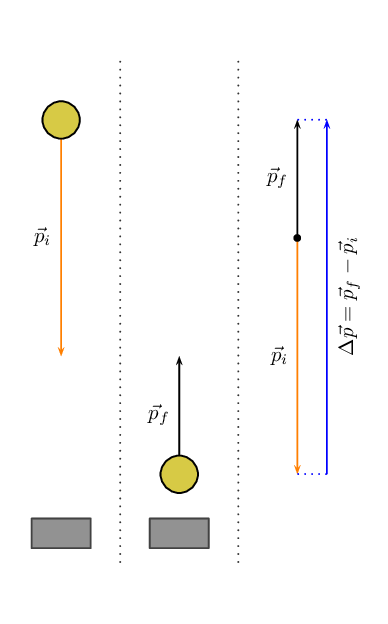
chapter. For example, a stationary basketball player bouncing a ball.

To illustrate the point, here is what the analysis would look like for a ball
bouncing off the floor:
Textbook Exercise 2.1
The fastest recorded delivery for a cricket ball is
\(\text{161,3}\) \(\text{km·hr$^{-1}$}\),
bowled by Shoaib Akhtar of Pakistan during a
match against England in the 2003 Cricket World
Cup, held in South Africa. Calculate the ball's
momentum if it has a mass of \(\text{160}\)
\(\text{g}\).
\[p = mv\]
\(v = \text{161,3}\text{ km·hr$^{-1}$}\) and \(m
= \text{160}\text{ g}\).
Converting the velocity to the correct S.I units:
\begin{align*}
v & = \text{161,3}\text{ km·hr$^{-1}$} \times
\frac{\text{1 000}\text{
m}}{\text{3 600}\text{ s}} \\
& = \text{44,81}\text{ m·s$^{-1}$}
\end{align*}
Converting the mass to the correct S.I units:
\begin{align*}
m & = \text{160}\text{ g} \times
\frac{\text{1}\text{ kg}}{\text{1 000}\text{ g}} \\
& = \text{0,16}\text{ kg}
\end{align*}
Therefore, computing the momentum:
\begin{align*}
p & = mv \\
& = (\text{0,16})(\text{44,81}) \\
& = \text{7,17}\text{ kg·m·s$^{-1}$}
\end{align*}
The fastest tennis service by a man is
\(\text{246,2}\) \(\text{km·hr$^{-1}$}\) by
Andy Roddick of the United States of America
during a match in London in 2004. Calculate the
ball's momentum if it has a mass of
\(\text{58}\) \(\text{g}\).
\[p = mv\]
\(v = \text{246,2}\text{ km·hr$^{-1}$}\) and \(m
= \text{58}\text{ g}\).
Converting the velocity to the correct S.I units:
\begin{align*}
v & = \text{246,2}\text{ km·hr$^{-1}$} \times
\frac{\text{1 000}\text{
m}}{\text{3 600}\text{ s}} \\
& = \text{68,39}\text{ m·s$^{-1}$}
\end{align*}
Converting the mass to the correct S.I units:
\begin{align*}
m & = \text{58}\text{ g} \times
\frac{\text{1}\text{ kg}}{\text{1 000}\text{ g}} \\
& = \text{0,058}\text{ kg}
\end{align*}
Therefore, computing the momentum:
\begin{align*}
p & = mv \\
& = (\text{0,058})(\text{68,39}) \\
& = \text{3,97}\text{ kg·m·s$^{-1}$}
\end{align*}
The fastest server in the women's game is Venus
Williams of the United States of America, who
recorded a serve of \(\text{205}\)
\(\text{km·hr$^{-1}$}\) during a match in
Switzerland in 1998. Calculate the ball's
momentum if it has a mass of \(\text{58}\)
\(\text{g}\).
\[p = mv\]
\(v = \text{205}\text{ km·hr$^{-1}$}\) and \(m =
\text{58}\text{ g}\).
Converting the velocity to the correct S.I units:
\begin{align*}
v & = \text{205}\text{ km·hr$^{-1}$} \times
\frac{\text{1 000}\text{
m}}{\text{3 600}\text{ s}} \\
& = \text{56,94}\text{ m·s$^{-1}$}
\end{align*}
Converting the mass to the correct S.I units:
\begin{align*}
m & = \text{58}\text{ g} \times \frac{\text{1}\text{
kg}}{\text{1 000}\text{ g}} \\
& = \text{0,058}\text{ kg}
\end{align*}
Therefore, computing the momentum:
\begin{align*}
p & = mv \\
& = (\text{0,058})(\text{56,94}) \\
& = \text{3,30}\text{ kg·m·s$^{-1}$}
\end{align*}
If you had a choice of facing Shoaib, Andy or Venus
and didn't want to get hurt, who would you
choose based on the momentum of each ball?
The ball with the smallest momentum gives you the
least chance of being hurt and so you would
choose to face Venus.














