Conservative and non-conservative forces (ESCMF)
In Grade 10, you saw that mechanical energy was conserved in the
absence of
non-conservative forces. It is important to know whether a force is an conservative
force or
an non-conservative force in the system, because this is related to whether the force
can
change an object's total mechanical energy when it does work on an object.
When the only
forces doing work are conservative forces (for example, gravitational
and spring forces), energy changes forms - from kinetic to
potential (or vice versa); yet the total amount of mechanical energy (\(E_K + E_P\)) is
conserved.
For example, as an
object falls in a gravitational field from a high elevation to a lower elevation,
some of the object's potential energy is changed into kinetic energy. However,
the sum of the kinetic and potential energies remain constant.
Non-conservative forces
We can investigate the effect of non-conservative forces on an object's total
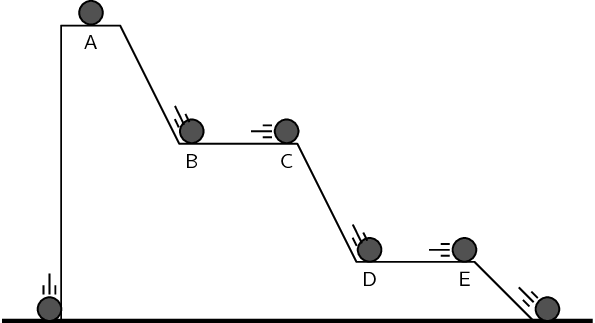
mechanical energy by rolling a ball along the floor from point A to point B.

Find a nice smooth surface (e.g. a highly polished floor), mark off two positions, A
and B, and roll the ball between them.
The total mechanical energy of the ball, at each point, is the sum of its kinetic
energy (\(E_k\)) and gravitational potential energy (\(E_p\)):
\begin{align*}
{E}_{\text{total},\text{A}}& = {E_k}_{,\text{A}}+{E_p}_{,\text{A}}\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}+mg{h}_{\text{A}}\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}+mg\left(0\right)\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}
\end{align*}\begin{align*}
{E}_{\text{total},\text{B}}& = {E_k}_{\text{B}}+{E_p}_{\text{B}}\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}+mg{h}_{\text{B}}\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}+mg\left(0\right)\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}
\end{align*}
In the absence of friction and other non-conservative forces, the ball should slide
along the floor and its speed should be the same at positions A and B.
Since there are no non-conservative forces acting on the ball, its total
mechanical energy at points A and B are equal.
\begin{align*}
{v}_{A}& = {v}_{\text{B}}\\
\frac{1}{2}m{v}_{\text{A}}^{2}& = \frac{1}{2}m{v}_{B}^{2}\\
{E}_{\text{total},\text{A}}& = {E}_{\text{total},\text{B}}
\end{align*}
Now, let's investigate what happens when there is friction (an non-conservative
force) acting on the ball.
Roll the ball along a rough surface or a carpeted floor. What happens to the speed of
the ball at point A compared to point B?
If the surface you are rolling the ball along is very rough and provides a large
non-conservative frictional force, then the ball should be moving much slower at
point B than at point A.
Let's compare the total mechanical energy of the ball at points A and B:
\begin{align*}
{E}_{\text{total},\text{A}}& = {\text{EK}}_{\text{A}}+{\text{PE}}_{\text{A}}\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}+mg{h}_{\text{A}}\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}+mg\left(0\right)\\
& = \frac{1}{2}m{v}_{\text{A}}^{2}
\end{align*}\begin{align*}
{E}_{\text{total},\text{B}}& = {\text{EK}}_{\text{B}}+{\text{PE}}_{\text{B}}\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}+mg{h}_{\text{B}}\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}+mg\left(0\right)\\
& = \frac{1}{2}m{v}_{\text{B}}^{2}
\end{align*}
However, in this case, \({v}_{A}\ne {v}_{B}\) and therefore
\({E}_{\text{total},\text{A}}\ne {E}_{\text{total},\text{B}}\). Since
\begin{align*}
{v}_{\text{A}}& > {v}_{\text{B}}\\
{E}_{\text{total},\text{A}}& > {E}_{\text{total},\text{B}}
\end{align*}
Therefore, the ball has lost mechanical energy as it moves across the carpet.
However, although the ball has lost mechanical energy, energy in the larger
system has still been conserved. In this case, the missing
energy is the work done by the carpet through applying a frictional force on the
ball. In this case the carpet is doing negative work on the ball.
When an non-conservative force (for example friction, air resistance, applied
force) does work on an object, the total mechanical energy (\(E_k + E_p\)) of that
object changes. If positive work is done, then the object will gain energy.
If negative work is done, then the object will lose energy.
When a net force does work
on an object, then there
is always a change in the kinetic energy
of the object. This is because the object experiences an acceleration and therefore
a change in velocity.
This leads us to the work-energy theorem.
The work-energy theorem is another example of the conservation of energy which
you saw in Grade 10.
Worked example 6: Work-energy theorem
A \(\text{1}\) \(\text{kg}\) brick is
dropped from a height of \(\text{10}\) \(\text{m}\).
Calculate the work that has been done on the brick between the moment it is
released
and the moment when it hits the ground. Assume that air resistance can be
neglected.
Determine what is given and what is required
-
Mass of the brick: \(m=\text{1}\text{ kg}\).
-
Initial height of the brick: \({h}_{i}=\text{10}\text{ m}\).
-
Final height of the brick: \({h}_{f}=\text{0}\text{ m}\).
-
We are required to determine the work done on the brick as it hits
the ground.
Determine how to approach the problem
The brick is falling freely, so energy is conserved. We know that the work done is
equal to the difference in kinetic energy. The brick has no kinetic energy at
the moment it is dropped, because it is stationary. When the brick hits the
ground, all the brick's potential energy is converted to kinetic energy.
Determine the brick's potential energy at \({h}_{i}\)
\begin{align*}
E_p& = m·g·h\\
& = \left(1\right)\left(\text{9,8}\right)\left(10\right)\\
& = \text{98}\text{ J}
\end{align*}
Determine the work done on the brick
The brick had \(\text{98}\) \(\text{J}\) of potential energy when it was released and
\(\text{0}\) \(\text{J}\) of kinetic energy. When the brick hit the ground, it
had \(\text{0}\) \(\text{J}\) of potential energy and \(\text{98}\) \(\text{J}\)
of kinetic energy. Therefore \({E}_{k,i}=\text{0}\text{ J}\) and
\({E}_{k,f}=\text{98}\text{ J}\).
From the work-energy theorem:
\begin{align*}
W_{\text{net}}& = \Delta E_k\\
& = {E}_{k,f}-{E}_{k,i}\\
& = 98-0\\
& = \text{98}\text{ J}
\end{align*}
Hence, \(\text{98}\) \(\text{J}\) of work was done on the brick.
Worked example 7: Work-energy theorem 2
The driver of a \(\text{1 000}\) \(\text{kg}\) car travelling at a speed of
\(\text{16,7}\) \(\text{m·s$^{-1}$}\) applies the car's brakes when he sees
a red light. The car's brakes provide a frictional force of
\(\text{8 000}\) \(\text{N}\). Determine the stopping distance of the car.
Determine what is given and what is required
We are given:
-
mass of the car: \(m = \text{1 000}\text{ kg}\)
-
speed of the car: \(v = \text{16,7}\text{ m·s$^{-1}$}\)
-
frictional force of brakes: \(\vec{F} = \text{8 000}\text{ N}\)
We are required to determine the stopping distance of the car.
Determine how to approach the problem
We apply the work-energy theorem. We know that all the car's kinetic energy is lost
to friction. Therefore, the change in the car's kinetic energy is equal to the
work done by the frictional force of the car's brakes.
Therefore, we first need to determine the car's kinetic energy at the moment of
braking using:
\(E_k=\frac{1}{2}m{v}^{2}\)
This energy is equal to the work done by the brakes. We have the force applied by the
brakes, and we can use:
\(W=F \Delta x \cos \theta\)
to determine the stopping distance.
Determine the kinetic energy of the car
\begin{align*}
E_k& = \frac{1}{2}m{v}^{2}\\
& = \frac{1}{2}\left(1000\right){\left(\text{16,7}\right)}^{2}\\
& = \text{139 445}\text{ J}
\end{align*}
Determine the work done
Assume the stopping distance is \({\Delta x}_{0}\). Since the direction of the
applied force and the displacement are in opposite directions, \(\theta =
180°\). Then the work done is:
\begin{align*}
W& = F \Delta x \cos \theta\\
& = \left(8000\right)\left( \Delta x_0 \right) \cos (180) \\
& = \left(8000\right)\left( \Delta x_0 \right)(-\text{1}) \\
& = \left(-\text{8 000}\right)\left( \Delta x_0 \right)
\end{align*}
Apply the work-enemy theorem
The change in kinetic energy is equal to the work done.
\begin{align*}
\Delta E_k& = W_{\text{net}}\\
{E}_{k,f}-{E}_{k,i}& = \left(-8000\right)\left({\Delta x_0}\right)\\
\text{0}-\text{139 445} & = \left(-8000\right)\left({\Delta x_0}\right)\\
\therefore \Delta x_0 & = \frac{139445}{8000}\\
& = \text{17,4}\text{ m}
\end{align*}
Write the final answer
The car stops in \(\text{17,4}\) \(\text{m}\).
Worked example 8: Block on an inclined plane [credit: OpenStax College]
A block of \(\text{2}\) \(\text{kg}\)
is pulled up along a smooth incline of length
\(\text{10}\) \(\text{m}\) and height
\(\text{5}\) \(\text{m}\)
by applying an non-conservative force. At the end of incline, the block is
released from rest to slide down
to the bottom. Find the
- work done by the non-conservative force,
- the kinetic energy of the
block at the end of round trip, and
- the speed at the end of the round trip.
Analyse what is given and what is required
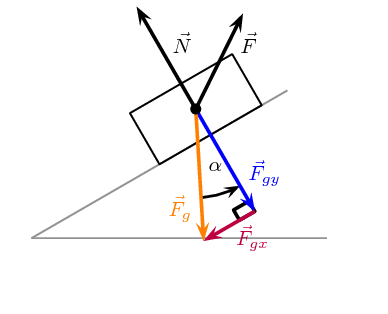
There are three forces on the block while going up:
- weight of the block, \(\vec{F}_g=m\vec{g}\),
- normal force, \(\vec{N}\), applied by the block and
- non-conservative force, \(\vec{F}\).
On the other hand, there are only two forces while going
down. The non-conservative force is absent in downward journey. The force diagram of
the forces is shown here for upward motion of the block.
Work done by non-conservative force during round trip
The work done by the non-conservative force we will call \(W_F\).
We have not been given a magnitude or direction for \(\vec{F}\),
all we do know is that it must result in the block moving up the slope.
We have represented
the non-conservative force on the force diagram with an arbitrary vector.
\(\vec{F}\) acts only during upward journey. Note that the
block is simply released at the end of the upward journey. We
need to find the work done by the non-conservative force only during the upward
journey.
\[W_F=W_{F\text{ (up)}}+W_{F\text{ (down)}}=W_{F\text{ (up)}}+0=W_{F\text{ (up)}}\]
The kinetic energies in the beginning and at the end of the motion up the slope
are zero.
We can conclude that sum of the work
done by all three forces is equal to zero during the upward motion. The change
in kinetic energy is zero which implies that the net work done is zero.
\begin{align*}
W_{\text{net}} & = W_{F(up)} + W_{g(up)} + W_{N(up)} \\
0 & = W_{F(up)} + W_{g(up)} + W_{N(up)}
\end{align*}
If we know the work done by the other two forces
(normal force and gravity), then we can calculate the work done by
the non-conservative force, \(F\), as required.
Work done by normal force during upward motion
The block moves up the slope, the normal force is perpendicular to the
slope and, therefore, perpendicular to the direction of motion.
Forces that are perpendicular to the direction of motion do no
work.
\begin{align*}
0 & = W_{F\text{ (up)}} + W_{g\text{ (up)}} + W_{N\text{ (up)}} \\
0 & = W_{F\text{ (up)}} + W_{g\text{ (up)}} + (0)\\
W_{F\text{ (up)}} & = - W_{g\text{ (up)}}
\end{align*}
Thus, we need to compute work done by the gravity in order to compute
work by the non-conservative force.
Work done by gravity during upward motion
The component of the force due to gravity that is perpendicular
to the slope, \(\vec{F}_{gy}\), will do no work so we only need to consider the
component
parallel to the slope, \(\vec{F}_{gx}\).
For the upward motion \(\vec{F}_{gx}\)
is in the opposite direction to the motion, therefore the angle between them is
\(\theta = 180°\), which means \(\cos \theta = -1\), so we expect to see
negative work is done.
The magnitude of \(\vec{F}_{gx}\) is \(F_{gx} = mg\sin\alpha\). So the work done by
gravity during the upward motion is :
\begin{align*}
W_{g\text{ (up)}}& = F_{gx} \Delta x \cos \theta \\
& = mg \sin\alpha\cdot\Delta x \cos \theta\\
&=(2)(\text{9,8})(\frac{5}{10})(10)\cos(180)\\
&=−\text{98}\text{ J}
\end{align*}
Be careful not to be confused by which angle has been labelled \(\alpha\) and
which \(\theta\). \(\alpha\) is
not the angle between the force and the direction of motion but the
incline of the plane in this
particular problem. It is important to understand which symbol
represents which physical quantity
in the equations you have learnt.
Hence, the work done by the non-conservative force during the round trip is:
\begin{align*}
W_F = W_{F\text{ (up)}} & = - W_{g\text{ (up)}} \\
=−(−\text{98})\\
=\text{98}\text{ J}
\end{align*}
Kinetic energy at the end of round trip
The kinetic energy at the end of the upward motion was zero but it is not
zero at the end of the entire downward motion.
We can use the work-energy theorem to analyse the whole motion:
\begin{align*}
W_{(round\ trip)} & = E_{k,f} - E_{k,i} \\
& = E_{k,f} - 0 \\
& = E_{k,f}
\end{align*}
To determine the net work done, \(W_{\text{ (round trip)}}\), we need to sum the work
done by each force acting during the period. We have calculated the work done by
\(\vec{F}\) already and we know that there is no work done by the normal force.
The total work done during round trip by gravity is the sum of the work done
during the upward motion (where the force is in the opposite direction to the
motion)
and the downward motion (where the force is in the same direction as the
motion).
The distance over which the force acts is the same during the upward and downward
motion and the magnitude of the force is the same. The only difference between
the
calculation for the work done during the upward and downward motion is the sign
because of the change of direction of the motion. Therefore:
\begin{align*}
W_{g\text{ (round trip)}} &=W_{g\text{ (up)}} + W_{g\text{ (down)}} \\
& = ( mg\sin\alpha \cdot \Delta x \cos 180°) + (mg\sin\alpha \cdot \Delta x
\cos 0°)\\
& = ( −mg\sin\alpha \cdot \Delta x) + (mg\sin\alpha \cdot\Delta x)\\
&= \text{0}\text{ J}
\end{align*}
Hence, the total work done during round trip is:
\begin{align*}
W_{(round\ trip)} & = W_{F} + W_{g} + W_{N} \\
& = W_{F} + W_{g(up)} + W_{N(up)} \\
& = (\text{98})+ (0) + (0) \\
& = \text{98}\text{ J}
\end{align*}
We can now use this in the equation for the work-energy theorem:
\begin{align*}
W_{(round\ trip)} & = E_{k,f} \\
E_{k,f} & =\text{98}\text{ J}
\end{align*}
Speed of the block
We know the kinetic energy of the block therefore we can determine its
speed:
\begin{align*}
E_{k,f} &= \frac{1}{2}mv^2 \\
\frac{1}{2}mv^2&= E_{k,f} \\
v &=\pm\sqrt{\frac{2}{m}E_{k,f}} \\
&=\pm\sqrt{\frac{2}{(2)}(\text{98})} \\
&=\pm\text{9,89949493661} \\
&=\text{9,90}\text{ m·s$^{-1}$}
\end{align*}
Note that the total work done during the
upward motion is zero as the block is stationary at the beginning and at the
end of the motion up the incline. The positive work done by the non-conservative
force is cancelled by the fact that exactly the same amount of negative work is
done by
gravity. The net work comes from the work done during the downward motion by
gravity.
Net work done results in a change in kinetic energy as per the work-energy
theorem.