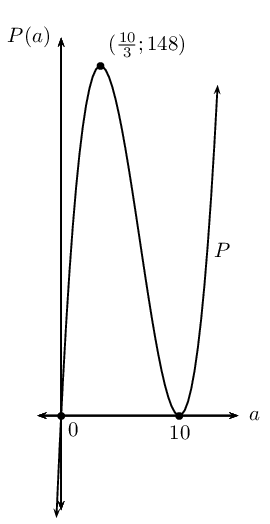
The sum of two positive numbers is \(\text{20}\). One of the
numbers is multiplied by the square of the other. Find
the numbers that make this product a maximum.
Let the first number be \(x\) and the second number be \(y\)
and let the product be \(P\). We get the following two
equations:
\begin{align*}
x + y & = 20 \\
xy^{2} & = P
\end{align*}
Rearranging the first equation and substituting into the
second gives:
\begin{align*}
P & = (20 - x)^{2}x \\
& = 400x - 40x^{2} + x^{3}
\end{align*}
Differentiating and setting to \(\text{0}\) gives:
\begin{align*}
P' & = 400 - 80x + 3x^{2} \\
0 & = 3x^{2} - 80x + 400 \\
& = (3x-20)(x-20)
\end{align*}
Therefore, \(x=20\) or \(x=\frac{20}{3}\).
If \(x=20\) then \(y=0\) and the product is a minimum, not a
maximum.
Therefore, \(x=\frac{20}{3}\) and \(y=20-\frac{20}{3} =
\frac{40}{3}\).
Therefore the two numbers are \(\frac{20}{3}\) and
\(\frac{40}{3}\) (approximating to the nearest integer
gives \(\text{7}\) and \(\text{13}\)).
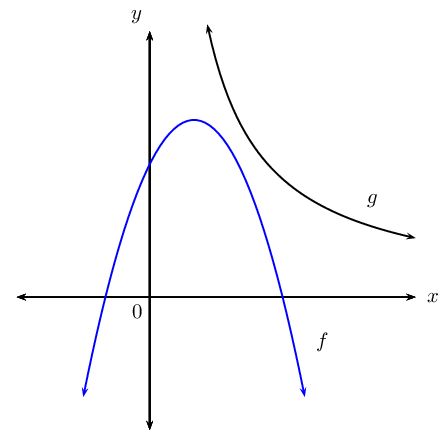
Determine the shortest vertical distance between the curves
of \(f\) and \(g\) if it is given that:
\begin{align*}
f(x)&= -x^{2}+2x+3 \\
\text{and } g(x)&= \frac{8}{x}, \quad x > 0
\end{align*}
\begin{align*}
\text{Let the distance } P(x) &= g(x) - f(x)\\
&=\frac{8}{x} - (-x^{2}+2x+3) \\
&=\frac{8}{x} +x^{2} - 2x - 3
\end{align*}
To minimise the distance between the curves, let \(P'(x) =
0:\)
\begin{align*}
P'(x) &= - \frac{8}{x^2 } + 2x - 2 \qquad (x \ne 0) \\
0 &= - \frac{8}{x^2 } + 2x - 2 \\
\therefore 0 &= - 8 + 2x^3 - 2x \\
0 &= 2x^3 - 2x - 8 \\
0 &= x^3 - x - 4 \\
0 &= (x - 2)(x^2 + x + 2) \\
\therefore x =2 & \text{ or } x = \frac{-1 \pm \sqrt{(1)^2 -
4(1)(2)}}{2(1)} \\
& \quad = \text{ no real solutions } \\
\therefore x & =2
\end{align*}
Therefore, the shortest distance:
\begin{align*}
P(2) &=\frac{8}{(2)} +(2)^{2} - 2(2) - 3 \\
&= 4 + 4 - 4 -3 \\
&= \text{1}\text{ unit}
\end{align*}
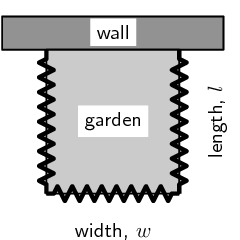
The diagram shows the plan for a verandah which is to be
built on the corner of a cottage. A railing \(ABCDE\) is
to be constructed around the four edges of the verandah.
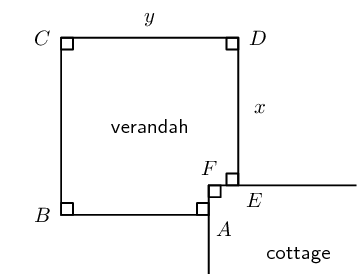
If \(AB=DE=x\) and \(BC=CD=y\), and the length of the railing
must be \(\text{30}\text{ m}\), find the values of \(x\)
and \(y\) for which the verandah will have a maximum
area.
We need to determine an expression for the area in terms of
only one variable.
The perimeter is:
\begin{align*}
P & = 2x + 2y \\
30 & = 2x + 2y \\
15 & = x + y \\
y&=15-x
\end{align*}
The area is:
\begin{align*}
A & = y^{2} - (y-x)^{2} \\
& = y^{2} - (y^{2} - 2xy + x^{2}) \\
& = y^{2} - y^{2} + 2xy - x^{2} \\
& = 2xy - x^{2}
\end{align*}
We use the expression for perimeter to eliminate the \(y\)
variable so that we have an expression for area in terms
of \(x\) only:
\begin{align*}
A(x) & = 2x(15-x) - x^{2} \\
& = 30x - 2x^{2} - x^{2} \\
& = 30x - 3x^{2}
\end{align*}
To find the maximum, we need to take the derivative and set
it equal to \(\text{0}\):
\begin{align*}
A'(x) & = 30 - 6x \\
0 & = 30 - 6x \\
6x & = 30 \\
x & = 5
\end{align*}
Therefore, \(x=\text{5}\text{ m}\) and substituting this
value back into the formula for perimeter gives
\(y=\text{10}\text{ m}\).
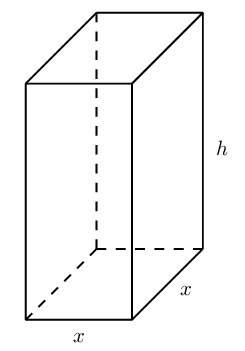
If the length of the sides of the base is \(x\) cm,
show that the total area of the cardboard needed
for one container is given by:
\[A (\text{in square centimetres}) =
\frac{\text{3 000}}{x} + 3x^{2}\]
\begin{align*}
V & = x^2h \\
750 & = x^2h \\
\therefore h & = \frac{750}{x^2}\\
A & = \text{ area of sides } + \text{ area of base }
+ \text{ area of top } \\
&= 4xh + x^2 + 2x^2 \\
&= 4xh + 3x^2 \\
\text{Substitute } h &= \frac{750}{x^2}: \\
A &= 4x\left( \frac{750}{x^2} \right) + 3x^2 \\
&= \frac{3000}{x}+ 3x^2
\end{align*}
Determine the dimensions of the container so that the
area of the cardboard used is minimised.
\begin{align*}
A(x) &= \frac{3000}{x}+ 3x^2 \\
A'(x) &= - \frac{3000}{x^2}+ 6x \\
\therefore 0 &= - \frac{3000}{x^2}+ 6x \\
6x &= \frac{3000}{x^2} \\
x^3 &= 500 \\
\therefore x &= \sqrt[3]{500} \\
&\approx \text{7,9}\text{ cm} \\
\therefore h & = \frac{750}{(\text{7,9})^2}\\
&\approx \text{12,0}\text{ cm}
\end{align*}