5.6 Summary | Polynomials

5.6 Summary (EMCGY)

Terminology:
Expression	A term or group of terms consisting of numbers, variables and the basic operators (\(+, -, \times, \div\)).
Univariate expression	An expression containing only one variable.
Root/Zero	A root, also referred to as the “zero”, of an equation is the value of \(x\) such that \(f(x)=0\) is satisfied.
Polynomial	An expression that involves one or more variables having different powers and coefficients. \(a_{n}x^{n} + \ldots + a_2x^{2} + a_{1}x + a_{0}, \text{ where } n \in \mathbb{N}_0\)
Monomial	A polynomial with one term. For example, \(7a^{2}b \text{ or } 15xyz^{2}\).
Binomial	A polynomial that has two terms. For example, \(2x + 5z \text{ or } 26 - g^{2}k\).
Trinomial	A polynomial that has three terms. For example, \(a - b + c \text{ or } 4x^2 + 17xy - y^3\).
Degree/Order	The degree, also called the order, of a univariate polynomial is the value of the highest exponent in the polynomial. For example, \(7p - 12p^2 + 3p^5 + 8\) has a degree of \(\text{5}\).

Quadratic formula: \(x = \frac{-b±\sqrt{{b}^{2}-4ac}}{2a}\)
Remainder theorem: a polynomial \(p(x)\) divided by \(cx - d\) gives a remainder of \(p\left(\dfrac{d}{c}\right)\).
Factor theorem: if the polynomial \(p(x)\) is divided by \(cx - d\) and the remainder, \(p \left( \frac{d}{c} \right)\), is equal to zero, then \(cx - d\) is a factor of \(p(x)\).
Converse of the factor theorem: if \(cx - d\) is a factor of \(p(x)\), then \(p \left( \frac{d}{c} \right) = 0\).
Synthetic division:

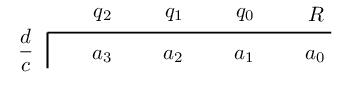
We determine the coefficients of the quotient by calculating:
\begin{align*} q_{2} &= a_{3} + \left( q_{3} \times \frac{d}{c} \right) \\ &= a_{3} \quad \text{ (since } q_{3} = 0) \\ q_{1} &= a_{2} + \left( q_{2} \times \frac{d}{c} \right) \\ q_{0} &= a_{1} + \left( q_{1} \times \frac{d}{c} \right) \\ R &= a_{0} + \left( q_{0} \times \frac{d}{c} \right) \end{align*}

temp text

Table of Contents