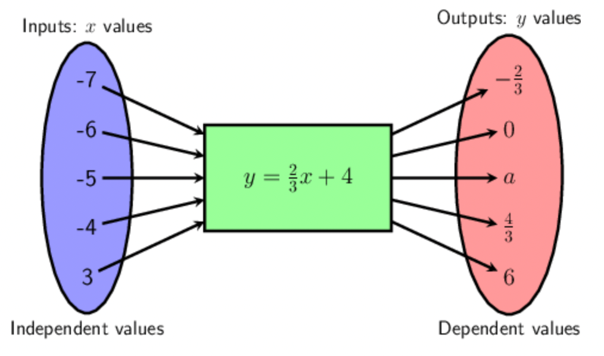
22.2 Working with equations and a table
We can use tables to solve equations – but we can also use equations to fill in a table of values. You
can think of tables as a way to compactly summarise information, such as input and output values that correspond
to each other.
For example, given the flow diagram below, we can show the same information using a table.
| \(x\) |
\(- 7\) |
\(- 6\) |
\(- 5\) |
\(- 4\) |
\(- 3\) |
| \(y\) |
\(- \frac{2}{3}\) |
\(0\) |
\(a\) |
\(\frac{4}{3}\) |
\(2\) |
The equation is \(y = \frac{2}{3}x + 4\). We can work out the missing output value like this:
\[\begin{align}
a &= \frac{2}{3}( - 5) + 4 \\
&= - \frac{10}{3} + 4 \\
&= - \frac{10}{3} + \frac{12}{3} \\
&= \frac{2}{3}
\end{align}\]
Can you see the pattern in \(y\)-values?
\[- \frac{2}{3}; 0; \frac{2}{3}; \frac{4}{3}; 2\]
| \(x\) |
\(- 7\) |
\(- 6\) |
\(- 5\) |
\(- 4\) |
\(- 3\) |
\(- 2\) |
| \(y\) |
\(- \frac{2}{3}\) |
\(0\) |
\(\frac{2}{3}\) |
\(\frac{4}{3}\) |
\(2\) |
\(?\) |
The common difference is \(\frac{2}{3}\), so it will be easy to find the next output value in this table if the
input is \(x = - 2\):
\[\begin{align}
2 + \frac{2}{3} &= 2\frac{2}{3} \\
&= \frac{8}{3}
\end{align}\]
Now, use the equation to check if this is true:
\[\begin{align}
y &= \frac{2}{3}x + 4 \\
&= \frac{2}{3}( - 2) + 4 \\
&= - \frac{4}{3} + 4 \\
&= - \frac{4}{3} + \frac{12}{3} \\
&= \frac{8}{3}
\end{align}\]
Yes! The pair of values \(\left( - 2; \frac{8}{3} \right)\) is a solution of the equation \(y = \frac{2}{3}x +
4\).
Number patterns and equations
Let’s do a quick revision of number patterns.
Exercise 22.1
Look at the table below and answer the questions that follow.
| Term number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
| Term value |
\(8\) |
\(13\) |
\(18\) |
\(23\) |
\(28\) |
\(33\) |
\(38\) |
\(43\) |
\(48\) |
-
Which of the following rules will produce the number pattern given in the second row of the table above?
- Term value = \(8n\) where \(n\) is the term number
- Term value = \(6n\ - \ 1\) where \(n\) is the term number
- Term value = \(6n\ + \ 2\) where \(n\) is the term number
- Term value = \(10n\ - \ 2\) where \(n\) is the term number
- Term value = \(5n\ + \ 3\) where \(n\) is the term number
-
The sixth term of the sequence has the value \(33\). Which term will have the value \(143\)? Set up and
solve an equation to find the answer.
- Pattern E
-
Term value \(= 5n + 3\). The term \(= 143\), so we solve for \(n\).
\[\begin{align}
143 &= 5n + 3 \\
143 - 3 &= 5n + 3 - 3 \\
140 &= 5n \\
140 \div 5 &= 5n \div 5 \\
\therefore 28 &= n
\end{align}\]
So the \(28^{\text{th}}\) term will have the value \(143\).
Look at the table below and answer the questions that follow.
| Term number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
| Term value |
\(5\) |
\(8\) |
\(11\) |
\(14\) |
\(17\) |
\(20\) |
\(23\) |
\(26\) |
\(29\) |
- Write the rule that will produce the number pattern in the second row of this table. You may have to
experiment to find out what the rule is.
- Which term will have the value \(221\)?
-
\(5 = 1\ \mathbf{\times\ 3 + 2}\); \(8 = 2\ \mathbf{\times\ 3 + 2}\); …; \(20 = 6\
\mathbf{\times\ 3 + 2}\); …
Experiment with input values to find out what the rule is for the output numbers.
Term value = \(n \times 3 + 2 = 3n + 2\)
-
\[\begin{align}
221 &= 3n + 2 \\
221 - 2 &= 3n + 2 - 2 \\
219 &= 3n \\
\therefore n &= 73
\end{align}\]
The rule for number pattern A is \(4n + 11\), and the rule for pattern B is \(7n - 34\).
-
Complete the table below for the two patterns.
| Term number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
| Pattern A |
|
|
|
|
|
|
|
|
|
| Pattern B |
|
|
|
|
|
|
|
|
|
- For which value of \(n\) are the terms of the two patterns equal?
-
| Term number |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
\(8\) |
\(9\) |
| Pattern A: \(4n + 11\) |
\(15\) |
\(19\) |
\(23\) |
\(27\) |
\(31\) |
\(35\) |
\(39\) |
\(43\) |
\(47\) |
| Pattern B: \(7n - 34\) |
\(- 27\) |
\(- 20\) |
\(- 13\) |
\(- 6\) |
\(1\) |
\(8\) |
\(15\) |
\(22\) |
\(29\) |
-
To find out when the terms are equal, you can keep on filling in the table following the given
patterns until you find that the values are the same. Another way to do it is to equate the two
expressions for the patterns and solve the equation:
\[\begin{align}
4n + 11 &= 7n - 34 \\
4n + 11 - 11 &= 7n - 34 - 11 \\
4n &= 7n - 45 \\
4n - 7n &= 7n - 45 - 7n \\
- 3n &= - 45 \\
\frac{- 3n}{- 3} &= \frac{- 45}{- 3} \\
\therefore n &= 15
\end{align}\]
Therefore the \(15^{\text{th}}\) terms of the two patterns will be the same. Check by continuing
the table.
Now that you have worked with some patterns, you can continue to work with equations and tables to find
solutions to the equations.
Worked Example 22.1: Working with equations and a
table
The equation \(y = \frac{3}{2}x - 3\) is represented by the table below. However, there is a number missing
from the output values.
| \(x\) |
\(- 5\) |
\(- 2\) |
\(- 1\) |
\(4\) |
\(5\) |
\(10\) |
| \(y\) |
\(- \frac{21}{2}\) |
\(- 6\) |
\(- \frac{9}{2}\) |
\(a\) |
\(\frac{9}{2}\) |
\(12\) |
- Find the value of \(a\).
- Verify whether \((2;0)\) is a solution to the equation, \(y = \frac{3}{2}x - 3\).
Find the missing output value.
This question asks us to find the output value for the equation \(y = \frac{3}{2}x - 3\) when \(x = 4\).
Let the equation show you the answer: substitute \(x = 4\) into the equation and calculate the missing
value, \(a\).
\[\begin{align}
y &= \frac{3}{2}x - 3 \\
&= \frac{3}{2}(4) - 3 \\
&= 6 - 3 \\
&= 3
\end{align}\]
The missing value from the table is the output value of \(a = 3\).
Find out whether the given
ordered pair is a solution to the equation.
You have an equation, and you must decide if \((2; 0)\) solves the equation. Remember that a solution for
the equation has values for \(x\) and \(y\) which “agree with” the equation. If you substitute
\(x = 2\) into the equation and the answer is \(y = 0\) then \((2; 0)\) is a solution to the equation;
otherwise it is not.
The only way to know is to give it a try:
\[\begin{align}
y &= \frac{3}{2}x - 3 \\
&= \frac{3}{2}(2) - 3 \\
&= 3 - 3 \\
&= 0
\end{align}\]
When you substitute \(x = 2\) into the equation, the output value is \(y = 0\). This is exactly what the
ordered pair said it should be, so the ordered pair agrees with the equation!
Therefore, the ordered pair \((2; 0)\) is a solution to the equation \(y = \frac{3}{2}x - 3\).
Worked Example 22.2: Working with equations and a
table
The equation, \(y = \frac{3}{4}x + 1\), is represented by the table below. However, there are two numbers
missing from the input values.
| \(x\) |
\(- 4\) |
\(- 2\) |
\(0\) |
\(1\) |
\(b\) |
\(c\) |
| \(y\) |
\(- 2\) |
\(- \frac{1}{2}\) |
\(1\) |
\(\frac{7}{4}\) |
\(7\) |
\(12\) |
- Find the values of \(b\) and \(c\).
- Verify whether \((24; 19)\) is a solution to the equation, \(y = \frac{3}{4}x + 1\).
This question asks us to find the input value for the equation \(y = \frac{3}{4}x + 1\) when \(x = b\) and
\(y = 7\).
Use the equation to find the answer: substitute \(x = b\) and \(y = 7\) into the equation and calculate the
missing value, \(b\).
\[\begin{align}
y &= \frac{3}{4}x + 1 \\
7 &= \frac{3}{4}(b) + 1 \\
7\ \mathbf{-\ 1} &= \frac{3}{4}b + 1\ \mathbf{-\ 1} \\
6 &= \frac{3}{4}b \\
6 \times \frac{4}{3} &= \frac{3}{4}b \times \frac{4}{3} \\
\therefore 8 &= b
\end{align}\]
The missing value from the table is the input value of \(b = 8\).
This question asks us to find the input value for the equation \(y = \frac{3}{4}x + 1\) when \(x = c\) and
\(y = 12\).
Use the equation to find the answer: substitute \(x = c\) and \(y = 12\) into the equation and calculate
the missing value, \(c\).
\[\begin{align}
y &= \frac{3}{4}x + 1 \\
12 &= \frac{3}{4}(c) + 1 \\
12\ \mathbf{-\ 1} &= \frac{3}{4}c + 1\ \mathbf{-\ 1} \\
11 &= \frac{3}{4}c \\
11 \times \frac{4}{3} &= \frac{3}{4}c \times \frac{4}{3} \\
\frac{44}{3} &= c \\
\therefore 14\frac{2}{3} &= c
\end{align}\]
The missing value from the table is the input value of \(c = \frac{44}{3}\) or \(c = 14\frac{2}{3}\).
Verify the given ordered pair as a
solution to the equation.
You have an equation, and you must decide if \((24; 19)\) solves the equation. Remember that a solution for
the equation has values for \(x\) and \(y\) which “agree with” the equation. If you substitute
\(x = 24\) into the equation and the answer is \(y = 19\), then \((24; 19)\) is a solution to the equation;
otherwise it is not.
\[\begin{align}
y &= \frac{3}{4}x + 1 \\
&= \frac{3}{4}(24) + 1 \\
&= 3(6) + 1 \\
&= 18 + 1 \\
&= 19
\end{align}\]
When you substitute \(x = 24\) into the equation, the output value is \(y = 19\). This is exactly what the
ordered pair said it should be, so the ordered pair agrees with the equation.
Therefore, the ordered pair \((24; 19)\) is a solution to the equation \(y = \frac{3}{4}x + 1\).
Exercise 22.1
The equation, \(y = 7x - 3\), is represented by the table below. However, there are two numbers missing from
the input values.
| \(x\) |
\(- 2\) |
\(- 1\) |
\(0\) |
\(\frac{1}{2}\) |
\(b\) |
\(c\) |
| \(y\) |
\(- 17\) |
\(- 10\) |
\(- 3\) |
\(\frac{1}{2}\) |
\(4\) |
\(60\) |
- Find the values of \(b\) and \(c\).
- Verify whether \((5;32)\) is a solution to the equation \(y = 7x - 3\).
-
For \(y = 4\), what is \(b\)?
\[\begin{align}
y &= 7x - 3 \\
4 &= 7b - 3 \\
7 &= 7b \\
\therefore 1 &= b
\end{align}\]
For \(y = 60\), what is \(c\)?
\[\begin{align}
y &= 7x - 3 \\
60 &= 7c - 3 \\
63 &= 7c \\
\therefore 9 &= c
\end{align}\]
-
\(\ (5;32)\) is a solution, because \(32 = 7(5) - 3 = 35 - 3\).
or
\[\begin{align}
y &= 7x - 3 \\
32 &= 7x - 3 \\
35 &= 7x \\
\therefore 5 &= x
\end{align}\]
The equation, \(y = x - \frac{2}{5}\), is represented by the table below. However, there are two numbers
missing from the input values.
| \(x\) |
\(- \frac{4}{5}\) |
\(a\) |
\(0\) |
\(\frac{1}{5}\) |
\(\frac{3}{5}\) |
\(b\) |
| \(y\) |
\(- \frac{6}{5}\) |
\(- \frac{3}{5}\) |
\(- \frac{2}{5}\) |
\(- \frac{1}{5}\) |
\(\frac{1}{5}\) |
\(\frac{3}{5}\) |
- Find the values of \(a\) and \(b\).
- Verify whether \(\left( \frac{3}{5};\frac{1}{5} \right)\) is a solution to the equation \(y = x -
\frac{2}{5}\).
-
For \(y = -\frac{3}{5}\), what is \(a\)?
\[\begin{align}
y &= x - \frac{2}{5} \\
- \frac{3}{5} &= a - \frac{2}{5} \\
- \frac{3}{5} + \frac{2}{5} &= a \\
\therefore - \frac{1}{5} &= a
\end{align}\]
For \(y = \frac{3}{5}\), what is \(b\)?
\[\begin{align}
\frac{3}{5} &= b - \frac{2}{5} \\
\frac{3}{5} + \frac{2}{5} &= b \\
\frac{5}{5} &= b \\
\therefore 1 &= b
\end{align}\]
-
\(\left( \frac{3}{5};\frac{1}{5} \right)\) is a solution to the equation, \(y = x - \frac{2}{5}\),
because \(\frac{1}{5} = \frac{3}{5} - \frac{2}{5}\).
The equation, \(y = \frac{1}{3}x + 2\), is represented by the table below. However, there are three numbers
missing from the input values.
| \(x\) |
\(- 3\) |
\(- 1\) |
\(a\) |
\(1\) |
\(b\) |
\(c\) |
| \(y\) |
\(1\) |
\(\frac{5}{3}\) |
\(2\) |
\(\frac{7}{3}\) |
\(\frac{8}{3}\) |
\(3\) |
- Find the values of \(a\), \(b\) and \(c\).
- Verify whether \((2;\frac{4}{3})\) is a solution to the equation \(y = \frac{1}{3}x + 2\).
-
Solve for \(a\):
\[\begin{align}
y &= \frac{1}{3}x + 2 \\
2 &= \frac{1}{3}a + 2 \\
0 &= \frac{1}{3}a \\
0 \times \frac{3}{1} &= \frac{1}{3}a \times \frac{3}{1} \\
\therefore 0 &= a
\end{align}\]
Solve for \(b\):
\[\begin{align}
\frac{8}{3} &= \frac{1}{3}b + 2 \\
\frac{8}{3} - \frac{2}{1} &= \frac{1}{3}b \\
\frac{8}{3} - \frac{6}{3} &= \frac{1}{3}b \\
\frac{2}{3} &= \frac{1}{3}b \\
\frac{2}{3} \times \frac{3}{1} &= \frac{1}{3}b \times \frac{3}{1} \\
\frac{6}{3} &= b \\
\therefore 2 &= b
\end{align}\]
Solve for \(c\):
\[\begin{align}
3 &= \frac{1}{3}c + 2 \\
3 - 2 &= \frac{1}{3}c \\
1 \times \frac{3}{1} &= \frac{1}{3}c \times \frac{3}{1} \\
\therefore 3 &= c
\end{align}\]
-
\((2;\frac{4}{3})\) is not a solution to the equation \(y = \frac{1}{3}x + 2\), because:
\[\begin{align}
RHS: \frac{1}{3}(2) + 2 &= \frac{2}{3} + \frac{6}{3} \\
&= \frac{8}{3} \\
\therefore RHS \neq LHS
\end{align}\]
The equation \(y = - 10x + \text{0,9}\) is represented by the table below. However, there is a number missing from
the input values.
| \(x\) |
\(a\) |
\(- 1\) |
\(0\) |
\(2\) |
| \(y\) |
\(\text{20,9}\) |
\(\text{10,9}\) |
\(\text{0,9}\) |
\(- \text{19,1}\) |
- Find the value of \(a\).
- Verify whether \((\text{2,5}; - \text{24,1})\) is a solution to the equation \(y = - 10x + 0,9\).
-
Solve for \(a\):
\[\begin{align}
y &= - 10x + \text{0,9} \\
\text{20,9} &= - 10a + \text{0,9} \\
\text{20,9} - \text{0,9} &= - 10a \\
20 &= - 10a \\
\therefore - 2 &= a
\end{align}\]
-
\((\text{2,5}; - \text{24,1})\) is a solution to the equation \(y = - 10x + 0,9\), because:
\[\begin{align}
RHS: - 10(\text{2,5}) + \text{0,9} &= - 25 + \text{0,9}\\
&= - \text{24,1} \\
\therefore RHS = LHS
\end{align}\]
The equation, \(y = 25x - 100\), is represented by the table below. However, there are two numbers missing
from the input values.
| \(x\) |
\(- 10\) |
\(- 5\) |
\(0\) |
\(b\) |
\(16\) |
\(c\) |
| \(y\) |
\(- 350\) |
\(- 225\) |
\(- 100\) |
\(150\) |
\(300\) |
\(400\) |
- Find the values of \(b\) and \(c\).
- Verify whether \((5;125)\) is a solution to the equation \(y = 25x - 100\).
-
Solve for \(b\):
\[\begin{align}
y &= 25x - 100 \\
150 &= 25b - 100 \\
150 + 100 &= 25b \\
250 &= 25b \\
250 \div 25 &= 25b \div 25 \\
\therefore 10 &= b
\end{align}\]
Solve for \(c\):
\[\begin{align}
400 &= 25c - 100 \\
500 &= 25c \\
500 \div 25 &= 25b \div 25 \\
\therefore 20 &= c
\end{align}\]
-
\((5;125)\) is not a solution to the equation \(y = 25x - 100\), because \(\lbrack 25(5) - 100 =
125 - 100 = 25\rbrack\), not \(125\).