16.4 Area and perimeter of rectangles
The opposite sides of a rectangle are equal in length. The perimeter of a rectangle is equal to the sum of the lengths of its four sides.
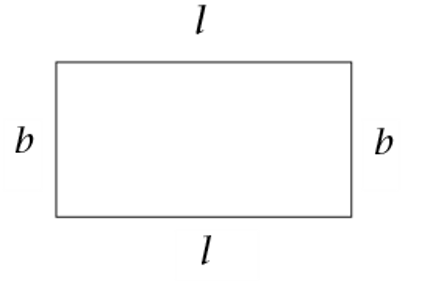
The area of a rectangle is equal to the product of its length and breadth.
\[\text{Area of a rectangle } = l \times b\]Worked example 16.8: Calculating the perimeter of a rectangle
Determine the perimeter of the rectangle. Express your answer in metres.
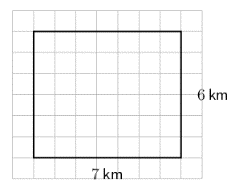
Calculate the perimeter of the rectangle.
Find the sum of all four sides of the rectangle.
\[\text{Perimeter of the rectangle } = 7 + 6 + 7 + 6 = 2 (7 + 6) = 2(13) = 26 \text{ km}\]Convert the units to give the answer in metres.
\(1 \text{ km} = 1\ 000 \text{ m}\), so we get \(26 \text{ km} = 26 \times 1\ 000 = 26\ 000 \text{ m}\).
Write the final answer.
\(\text{Perimeter of the rectangle } = 26\ 000 \text{ m}\).
Worked example 16.9: Calculating the area of a rectangle
Calculate the area of the rectangle.
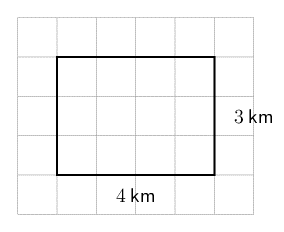
Calculate the area of the rectangle.
To calculate the area if the rectangle, we use the formula:
\[\begin{align} \text{Area of the rectangle } &= l \times b \\ &= 4 \times 3 \\ &= 12 \end{align}\]Write the final answer.
\(\text{Area of the rectangle} = 12 \text{ km}^2\).
