16.5 Area and perimeter of triangles
The perimeter of a triangle is the sum of the lengths of its three sides.
For a scalene triangle with three sides of different lengths:
\[\text{Perimeter } = a + b + c\]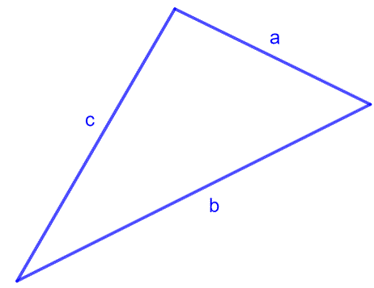
For an isosceles triangle with two sides of equal length:
\[\text{Perimeter } = 2a + b\]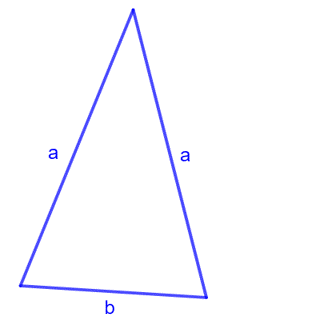
For an equilateral triangle with all three sides equal in length:
\[\text{Perimeter } = 3a\]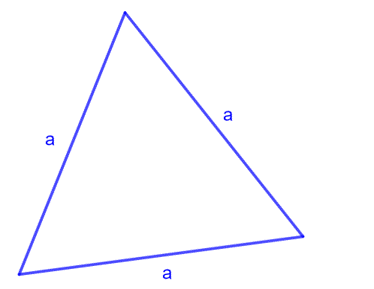
Worked example 16.10: Calculating the perimeter of a triangle
Find the perimeter of the triangle.

Calculate the perimeter of the triangle.
The triangle is a scalene triangle with three sides of different lengths.
\[\text{Perimeter } = 7 + 8 + 9 = 24 \text{ cm}\]Write the final answer.
\(\text{Perimeter of the triangle} = 24 \text{ cm}\).
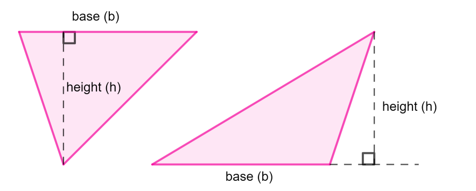
The formula for the area of a triangle is half the length of the base (\(b\)) times the perpendicular height (\(h\)) of the triangle.
Area of a triangle \(= \frac{1}{2} (b \times h)\)
We can choose any side of a triangle to be the base of the triangle. The perpendicular height of a triangle is the perpendicular line drawn from the opposite vertex to the base of the triangle. If a triangle is an obtuse-angled triangle, we can extend the base of the triangle so that the perpendicular height can be drawn.
Worked example 16.11: Calculating the area of a triangle by extending the base
Calculate the area of \(\triangle DEF\).
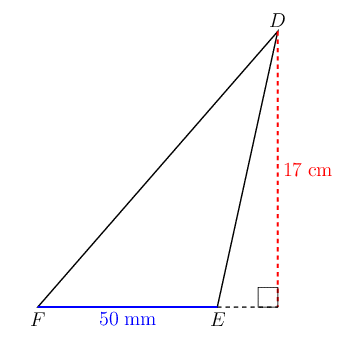
Convert the lengths to the same unit.
The diagram shows that \(FE = 50 \text{ mm}\) and \(DE = 17 \text{ cm}\). Before we can calculate the area of the triangle, we need to convert the lengths to the same unit.
\(10 \text{ mm} = 1 \text{ cm}\), so we can divide \(FE\) by \(10\) to get a length in centimetres:
\[FE = 50 \text{ mm} = \frac{50}{10} = 5 \text{ cm}\]Calculate the area of the triangle.
\[\begin{align} \text{Area of a triangle } &= \frac{1}{2} (b \times h) \\ \text{Area } \triangle DEF &= \frac{1}{2} (5 \times 17) \\ &= \text{42,5} \end{align}\]Write the final answer.
\(\text{Area } \triangle DEF = \text{42,5} \text{ cm}^2\).
Worked example 16.12: Calculating the area of a triangle using the correct perpendicular height
In \(\triangle XYZ\), \(YZ = \text{7} \text{ cm}, YT = \text{6,5} \text{ cm}\) and \(XS = \text{6} \text{ cm}\). Determine the area of \(\triangle XYZ\).
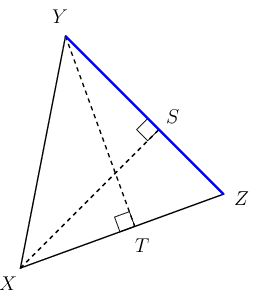
Identify the perpendicular height of the triangle for base \(YZ\).
We know the length of the side \(YZ\) so we can take \(YZ\) to be the base of the triangle. Vertex \(X\) lies opposite the base \(YZ\), so the correct perpendicular height for base \(YZ\) is \(XS\).
Note that \(YT\) is the perpendicular height of the triangle for base \(XZ\).
Calculate the area of the triangle.
\[\begin{align} \text{Area of a triangle } &= \frac{1}{2} (b \times h) \\ \text{Area } \triangle XYZ &= \frac{1}{2} (7 \times 6) \\ &= 21 \end{align}\]Write the final answer.
\(\text{Area } \triangle XYZ = 21 \text{ cm}^2\).
