16.7 Area and perimeter of complex shapes
Worked example 16.17: Calculating the area and perimeter of complex shapes
Determine the perimeter and area of the given shape. All lengths are measured in metres.
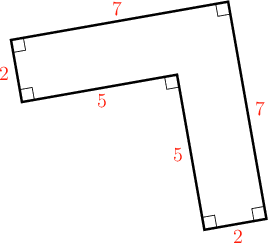
Determine the perimeter of the shape.
To find the perimeter of the shape, we need to find the sum of the lengths of the sides. Choose a starting point on the shape and then add the lengths of the sides:
Starting at the top right corner and moving in a clockwise direction:
\[\text{Perimeter } = 7 + 2 + 5 + 5 + 2 + 7 = 28\]The perimeter of the shape is \(28 \text{ m}\).
Find the area of the shape.
To calculate the area, we divide the shape into two rectangles.
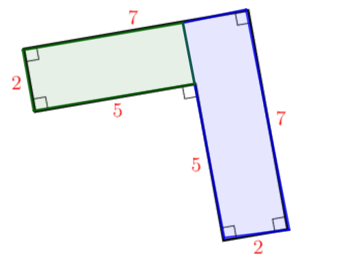
The area of the shape is \(24 \text{ m}^2\).
Write the final answer.
The perimeter of the shape is \(28 \text{ m}\) and the area is \(24 \text{ m}^2\).
Worked example 16.18: Calculating the area of a polygon
In the diagram below, \(WZ = 12 \text{ m}, YZ = 5 \text{ m}, XY = 8 \text{ m}\), and \(WY = 13 \text{ m}\). Calculate the area and perimeter of quadrilateral \(WXYZ\). Give your answer correct to one decimal place.
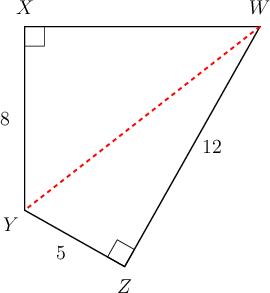
Divide the shape into two right-angled triangles.
We can divide the area of the quadrilateral into two right-angled triangles, \(\triangle WXY\) with \(\angle X = 90°\) and \(\triangle WYZ\) with \(\angle Z = 90°\).
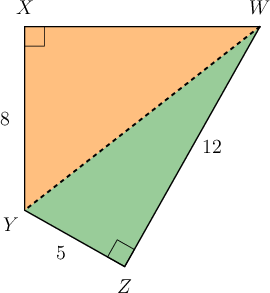
Calculate the area of \(\triangle WYZ\).
\[\begin{align} \text{Area of } \triangle WYZ &= \frac{1}{2}(b \times h) \\ &= \frac{1}{2}(5 \times 12) \\ &= \frac{1}{2}60 \\ &= 30 \\ \text{Area of } \triangle WYZ &= 30 \text{ m}^2 \end{align}\]Calculate the area of \(\triangle WXY\).
For this triangle, we do not know the perpendicular height (\(XW\)), so we need to use the theorem of Pythagoras to calculate the length of \(XW\):
\[\begin{align} WX^2 + XY^2 &= WY^2 \text{ (Pythagoras)} \\ WX^2 &= WY^2 − XY^2 \\ &= 13^2 − 8^2 \\ &= 169 − 64 \\ &= 105 \\ \therefore WX &= \sqrt{105} \end{align}\]Now that we know the perpendicular height, we can calculate the area of \(\triangle WXY\):
\[\begin{align} \text{Area of } \triangle WXY &= \frac{1}{2}(b \times h) \\ &= \frac{1}{2}(8 \times \sqrt{105}) \\ &= 4 \sqrt{105} \\ &= 4 \sqrt{105} = \text{40,9} \text{ m}^2 \end{align}\]