16.6 Area and perimeter of circles
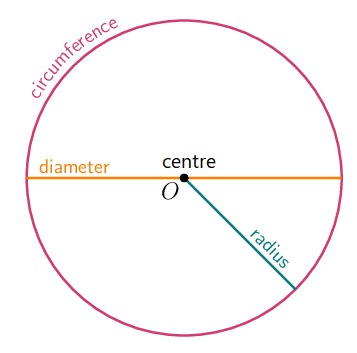
Parts of a circle
- The perimeter of a circle is called its circumference.
- The centre of a circle is the point inside the circle that is the same distance (that is, it is equidistant) from all points on the circumference of the circle.
- A line segment drawn from one point on the circumference to another point on the circumference that passes through the centre is called a diameter.
- A line segment from the centre of the circle to a point on the circumference is called a radius.
- The diameter of a circle is equal to twice its radius (\(d = 2r\)).
- circumference
- the perimeter of a circle
- centre of a circle
- the point inside the circle that is equidistant from all points on the circumference of the circle
- diameter
- a line segment drawn from one point on the circumference to another point on the circumference that passes through the centre of a circle
- radius
- a line segment from the centre of the circle to a point on the circumference
The relationship between the circumference and the diameter of a circle
For this investigation, you will need a pencil, paper and a measuring tape (or a piece of string and a ruler). You will also need five round or cylindrical objects to measure. For example, a round mug, a bowl, a toilet roll, a round lid, or a round jar.
Question 1
- Use your measuring tape (or string and ruler) to measure the circumference of each object. Be as accurate as possible.
- Use a measuring tape to measure the diameter of each object. Again, try to be as accurate as possible. Note that, for each object, the circumference and the diameter must be measured in the same unit of length.
- Copy and complete the table.
- For the last column of each row, divide the circumference by the diameter. Record each answer correct to three decimal places.
The first row has been completed as an example.
| Object | Description | Circumference | Diameter | \(\frac{\text{Circumference}}{\text{Diameter}}\) |
|---|---|---|---|---|
| Example: Bowl | Round breakfast bowl | \(\text{47,5} \text{ cm}\) | \(\text{15} \text{ cm}\) | \(\frac{\text{47,5}}{\text{15}} = \text{3,167}\) |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
Question 2
- What do you notice about the values in the last column of the table?
- What can you deduce from this investigation about the circumference of a circle divided by its diameter?
From the previous investigation, you should have noticed that there is a special relationship between the circumference of a circle and its diameter. For a circle of any size, the ratio of the circumference to its diameter is a constant value. This constant value is called pi (symbol \(\pi\)). Pi is an irrational number and when written as a decimal number, it has an infinite number of decimal places \(\text{3,141592654} \dots\) . Can you find the \(\pi\) function on your calculator?
- pi
- an irrational number that represents the ratio of the circumference of a circle to its diameter (symbol \(\pi\))
For everyday use in calculations, we use an approximate rational value of \(\pi\). We can use the fraction \(\frac{22}{7}\) or the decimal number \(\text{3,14}\).
Circumference of a circle
We have seen that the ratio of the circumference of a circle to its diameter is equal to the constant value \(\pi\). We can express this mathematically as:
\[\frac{C}{d} = \pi\]where \(C\) is the circumference and \(d\) is the diameter of a circle.
If we know the diameter of a circle, then we can use this formula to determine the circumference.
\[C = \pi \times d = \pi d\]We know that the diameter of a circle is equal to twice its radius, so we can also express the circumference of a circle in terms of its radius:
\[C = \pi d = \pi \times (2r) = 2 \pi r\]Worked example 16.13: Calculating the circumference of a circle
The circle below has a diameter of \(\text{8} \text{ m}\).
Calculate the circumference of the circle. Use \(\pi = \text{3,14}\) for your calculations.

Substitute the known values into the formula for circumference.
The question states that we must use \(\pi = \text{3,14}\) for our calculations and the diameter of the circle is \(d = 8\).
\[\begin{align} C &= \pi \times d \\ &= \text{3,14} \times 8 \\ &= \text{25,12} \end{align}\]Write the final answer.
Always remember to write your answer with the correct units.
The circumference of the circle is \(\text{25,12} \text{ m}\).
If we know the circumference of a circle, we can use the formula \(C = \pi d\) to determine the diameter of the circle. We divide both sides of the equation by \(\pi\) to get \(d\) on its own:
\[\begin{align} C &= \pi d \\ \frac{C}{\pi} &= \frac{\pi d}{\pi} \\ \frac{C}{\pi} &= d \end{align}\]So to find the diameter of a circle, we divide the circumference of the circle by \(\pi\):
\[d = \frac{C}{\pi}\]Worked example 16.14: Calculating the radius of a circle from the circumference
The circumference of a circle is \(24 \text{ cm}\). Find the radius of the circle. Give your answer correct to two decimal places.
Substitute known values into the formula for the diameter of a circle.
We know that the circumference of the circle is \(\text{24} \text{ cm}\). The question does not specify which value for \(\pi\) we must use, so we choose \(\text{3,14}\).
\[\begin{align} d &= \frac{C}{\pi} \\ &= \frac{\text{24}}{\text{3,14}} \\ &= \text{7,64} \end{align}\]Write the final answer.
We know that \(d = 2r\), so we can write:
\[\begin{align} r &= \frac{d}{2} \\ &= \frac{\text{7,64}}{2} \\ &= \text{3,82} \end{align}\]The radius of the circle is \(\text{3,82} \text{ cm}\).
Area of a circle
Area of a circle
For this investigation, you will need a pencil, paper, compass, scissors, glue and a ruler. You will also need two colour pencils. If you don’t have a compass, then you will need a round object that you can trace around to draw a circle.
Read all the instructions carefully before starting the investigation.
Question 1
- Draw a circle on a piece of paper.
- Cut out the circle.
- Fold the circle in half to get a semi-circle.
- Fold the semi-circle in half again to get a quarter circle.
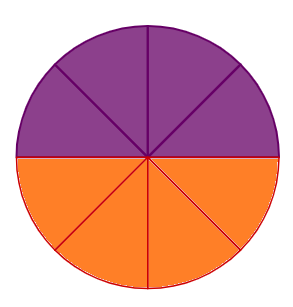
- Fold the quarter circle in half again to divide the circle into eighths.
- Unfold the piece of paper to get a full circle again. The fold lines should divide the circle into eight equal sectors.
- Mark the centre of the circle.
- Measure the radius of the circle.
- Fill in the top half of the circle using one colour and the bottom half of the circle using a different colour.
The diagram below shows the top four sectors in purple and the bottom four sectors in orange.
Question 2
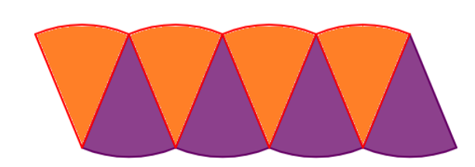
- Cut along the fold lines so that you have four orange sectors and four purple sectors.
- Arrange the sectors as shown in the diagram below. Use glue to keep the sectors in place.
- What type of quadrilateral does this shape look like?
Question 3
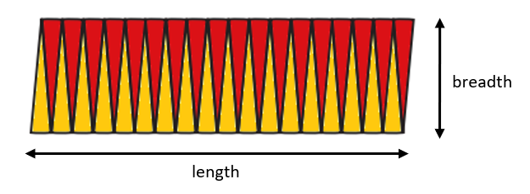
- The diagram below shows a circle that has been divided into \(36\) sectors. What type of quadrilateral does this shape look like?
- Can you express the approximate length in terms of circumference of the circle?
- Can you express the approximate breadth in terms of the radius of the circle?
- What is the formula for the area for this type of quadrilateral?
- Can you express the area of this quadrilateral in terms of circumference of the circle and its radius?
- Use your answers to deduce a formula for the area of a circle.
From the investigation, you should have discovered that the area of a circle is equal to half the circumference of the circle times its radius:
\[\begin{align} \text{Area of a circle } &= r \times \frac{1}{2}(\pi d) \\ \text{Substitute }d &= 2r \\ \text{Area of a circle } &= r \times \frac{1}{2} \pi (2r) \\ &= r \times \pi r \\ &= \pi r^2 \end{align}\]Worked example 16.15: Calculating the area of a circle
Calculate the area of a circle with a diameter of \(28 \text{ mm}\). Use \(\pi = \frac{22}{7}\).
Find the radius of the circle.
We know that \(d = 2r\). The diameter of the circle is \(28 \text{ mm}\), so the radius \(= \frac{1}{2} \times 28 = 14 \text{ mm}\).
Calculate the area of the circle.
\[\begin{align} \text{Area of a circle } &= \pi r^2 \\ &= \frac{22}{7} \times (14)^2 \\ &= \frac{22}{7} \times 196 \\ &= 616 \end{align}\]Write the final answer.
The area of the circle is \(616 \text{ mm}^2\).
Worked example 16.16: Calculating the diameter of a circle from the area
The area of a circle is \(\text{30} \text{ cm}^2\). Determine the diameter of the circle.
Use \(\pi = \text{3,14}\) and give your answer correct to one decimal place.
Use the area of the circle to find the length of the radius.
\[\begin{align} \text{Area of a circle } &= \pi r^2 \\ \text{30} &= \text{3,14} \times r^2 \end{align}\]We divide both sides of the equation by \(3,14\):
\[\frac{\text{30}}{\text{3,14}} = r^2\]We take the square root of both sides of the equation to get a value for \(r\):
\[\begin{align} r &= \sqrt{\frac{30}{3,14}} \\ \therefore r &= \sqrt{\text{9,55}} \end{align}\]Determine the diameter of the circle.
We know that \(d = 2r\).
\[\begin{align} \therefore d &= 2 \times \sqrt{\text{9,55}} \\ &= 2 \times \text{3,09} \\ &= \text{6,18} \\ \end{align}\]Write the final answer.
The diameter of the circle is \(\text{6,2} \text{ cm}\).
