13.2 Representing fractions
Instead of writing “four sevenths”, we may write \(\frac{4}{7}\). This is called common fraction notation.
The number \(7\) below the line is called the denominator and it shows that the whole was divided into \(7\) equal pieces. Therefore, each piece is \(1\) seventh of the whole. The denominator shows the unit in which the number is expressed.
The number \(4\) above the line is called the numerator and it indicates the number of pieces.
- common fraction
- a fraction in which both the numerator and the denominator are integers
- numerator
- the number above the line in a fraction that tells how many parts of the whole are used
- denominator
- the number below the line in a fraction that tells how many parts there are in the whole
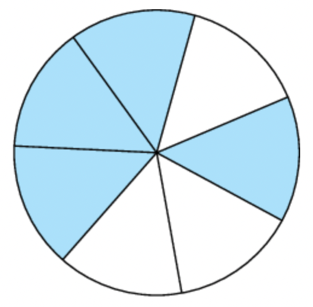
We can show a fraction using a diagram. Using a circle, we show the denominator as the total number of slices the circle is divided into, and the numerator as the number of shaded or unshaded slices.
We can also group the number of parts in a diagram to show different fractions. For example, this rectangle is divided into \(6\) identical squares:
If we shade \(4\) out of \(6\) squares, we can say that the shaded part represents \(\frac{4}{6}\) and the unshaded part represents \(\frac{2}{6}\).
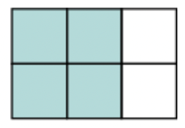
We can also say that \(2\) out of the \(3\) parts are shaded. We shade \(2\) in every \(3\) parts of the rectangle. So the shaded part represents \(\frac{2}{3}\) and the unshaded part represents \(\frac{1}{3}\).
We call these fractions equivalent, so \(\frac{4}{6} = \frac{2}{3}\) and \(\frac{2}{6} = \frac{1}{3}\).
The same fraction can be expressed in different forms. For example, the fraction \(\frac{3}{4}\) can be expressed in eighths as \(\frac{6}{8}\), in twentieths as \(\frac{15}{20}\), in sixtieths as \(\frac{45}{60}\), and in many other units.
These are all different ways of expressing the same fraction. They are called equivalent fractions.
Equivalent fractions allow us to write the same number in different ways.
\[\frac{3}{4} = \frac{6}{8} = \frac{15}{20} = \frac{45}{60}\]- equivalent fractions
- two or more fractions that represent the same amount (or value)
Equivalent fractions are the same value written in two or more different ways. It is exactly the same when we write \(4\) and \(\frac{4}{1}\). The values are the same – they only look different.
Worked example 13.1: Showing equivalent fractions in a diagram
Are the following fractions equivalent fractions or not?
\(\frac{2}{3}\) and \(\frac{6}{9}\)
Represent each fraction in a diagram.
Hint: You can either use a rectangle or a circle. We will use a rectangle in this example.
The rectangle at the top shows the fraction \(\frac{2}{3}\); the rectangle at the bottom shows \(\frac{6}{9}\).
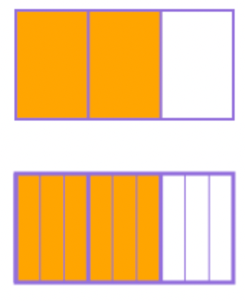
Compare the diagrams and draw a conclusion about the fractions.
Each of the three pieces of the top rectangle has been split into three more pieces in the rectangle at the bottom, but you can see from the picture that the fractions are the same size, because the shaded area is the same. Therefore \(\frac{2}{3}\) and \(\frac{6}{9}\) are equivalent.
Worked example 13.2: Equivalent fractions in a diagram
Are the following fractions equivalent fractions or not?
\(\frac{2}{5}\) and \(\frac{8}{20}\)
Represent each fraction in a diagram.
Hint: You can either use a rectangle or a circle. We will use a circle in this example.
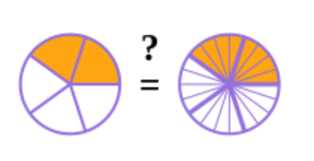
Compare the diagrams and draw a conclusion about the fractions.
The circle on the left shows the fraction \(\frac{2}{5}\); the circle on the right shows \(\frac{8}{20}\). Each of the pieces from the left circle has been split into four pieces in the circle on the right.
You can see from the picture that the fractions are the same size, because the shaded area is the same. Therefore \(\frac{2}{5}\) and \(\frac{8}{20}\) are equivalent.
Simplifying fractions
Simplifying a fraction means reducing the numbers in the fraction to the smallest possible numbers. We do this by cancelling a common factor from the numerator and the denominator. For example, in the fraction \(\frac{4}{6}\), both the numerator \(4\) and the denominator \(6\) are divisible by \(2\).
\(2\) is the common factor of \(4\) and \(6\); it is also the highest common factor.
\[\frac{4}{6} = \frac{2\ \mathbf{\times\ 2}}{3\ \mathbf{\times\ 2}} = \frac{2}{3} \times \frac{\mathbf{2}}{\mathbf{2}} = \frac{2}{3}\]Worked example 13.3: Using common factors to simplify fractions
Consider the following fraction:
\[\frac{21}{27}\]- What is the highest common factor in the numerator and denominator?
- Simplify the fraction.
Find the highest common factor.
The fraction in this question has a common factor in the numerator and denominator. We want the highest common factor (HCF) of the numerator and the denominator.
In this case, the highest common factor is \(3\). You can see this factor by rewriting the numbers in the fraction like this:
\[\frac{21}{27} = \frac{7 \times 3}{9 \times 3}\]The highest common factor in the numerator and denominator is \(3\).
Simplify the fraction.
Once you have the common factor, you can cancel those factors. The key thing is to realise that \(\frac{3}{3}\) cancels to make \(1\), which goes like this:
\[\frac{7 \times 3}{9 \times 3} = \frac{7}{9} \times \frac{3}{3} = \frac{7}{9}\]The simplified fraction is \(\frac{7}{9}\).
You can see this in a diagram too. The circle on the left shows the fraction \(\frac{21}{27}\), and the circle on the right shows the fraction \(\frac{7}{9}\). You can see that the shaded areas are the same: the fractions are equal (equivalent), but \(\frac{7}{9}\) is simplified because it has the smallest possible numbers.
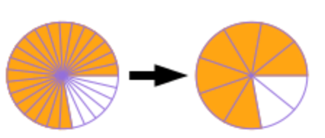
Worked example 13.4: Simplifying negative fractions
Consider the following fraction:
\[- \frac{20}{100}\]Simplify by dividing by the HCF.
The fraction is negative, but that really has nothing to do with simplifying the fraction: just do not lose the negative along the way!
In this case, there is a factor of \(20\) in both parts of the fraction, and you can cancel them. Remember that “cancel” means that they leave \(1\) behind when divided by each other.
\[- \frac{20}{100} = - \frac{1 \times 20}{5 \times 20} = - \frac{1}{5} \times \frac{20}{20} = - \frac{1}{5}\]Different types of fractions
You will find three types of fractions in fraction problems. Here is a summary of the three types:
- Proper fractions have a value of less than one; the numerator is always less than the denominator.
- Improper fractions are greater than or equal to one; the numerator is larger than or equal to the denominator.
- Mixed numbers (also called mixed fractions) have an integer part and a fraction part; the fraction part must be a proper fraction (less than one). We can write a mixed number as a sum of its integer part and the fractional part: \(2\frac{3}{5} = 2 + \frac{3}{5}\).
- proper fraction
- a fraction that has a value of less than one; the numerator is less than the denominator
- improper fraction
- a fraction that has a numerator larger than the denominator
- mixed number
- a number that is made up of a whole number and a fraction
Converting mixed numbers to common fractions for calculations
To convert a mixed number to an improper fraction, start with the denominator; then follow the solid arrow around and multiply by the integer in the front; then continue to follow the dashed arrow, and add the numerator.
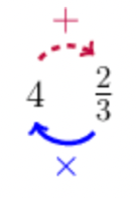
In other words, do this: \(3 \times 4 + 2 = 14\). This calculation gives you the numerator of the improper fraction.
Once we have the numerator, we must write the improper fraction using the same denominator as the mixed number, which gives us the answer:
\[4\frac{2}{3} = \frac{14}{3}\]It is important to know that these are really just two different ways of writing the same number!
Worked example 13.5: Converting mixed numbers to improper fractions
Convert the following mixed number to an improper fraction.
\[2\frac{3}{4}\]Calculate the numerator of the improper fraction.
\[4 \times 2 + 3 = 8 + 3 = 11\]Write the improper fraction.
Once we have the numerator, we must write the improper fraction using the same denominator as the mixed number, which gives us this answer:
\[2\frac{3}{4} = \frac{11}{4}\]The correct improper fraction is \(\frac{11}{4}\).
To convert an improper fraction to a mixed number, divide the numerator by the denominator.
Remember that the fraction bar is also a division symbol, so this fraction is a division problem:
\[\frac{5}{2} = 5 \div 2\]Start by finding out how many times \(2\) fits into \(5\): \(2 \times 2 = 4\), which is \(1\) less than \(5\). (In other words, when you divide \(5\) by \(2\), there is an “extra” \(1\) left over that did not come out of the \(5\).)
When we put it all together it comes out like this:
\[\frac{5}{2} = 2\frac{1}{2}\]Worked example 13.6: Converting improper fractions to mixed numbers
Convert the following improper fraction to a mixed number.
\[\frac{25}{9}\]Divide the numerator by the denominator.
You must change the improper fraction into a mixed number, so you solve a division problem:
\[\frac{25}{9} = 25 \div 9\]Start by finding out how many times \(9\) fits into \(25\).
\(9 \times 2 = 18\), which is \(7\) less than \(25\). (In other words, when you divide \(25\) by \(9\), there is an “extra” \(7\) left over that did not come out of the \(25\).)
Put the integer part and the fraction together.
When we put it all together, it comes out like this:
\[\frac{25}{9} = 2\frac{7}{9}\]The correct mixed number is \(2\frac{7}{9}\).
Fractions on a number line
We can locate fractions on a number line.
- All proper fractions are placed between \(0\) and \(1\) (or \(0\) and \(−1\) in the case of negative fractions).
In the diagram below, the dot shows where we reach \(7\) parts out of \(10\) pieces, which is the fraction \(\frac{7}{10}\).
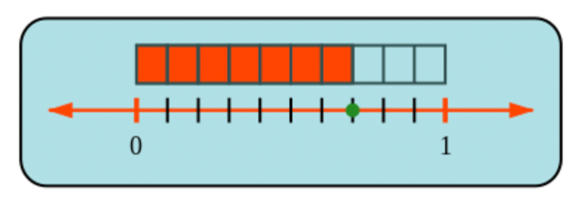
In the diagram below, the dot shows where we reach \(3\) parts out of \(5\) pieces, which is the fraction \(\frac{3}{5}\).
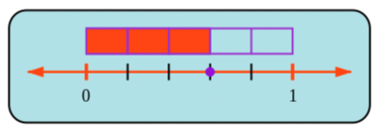
Placing fractions on a number line helps when we compare fractions.
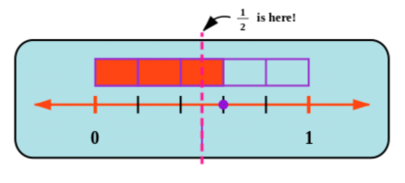
For example, to decide whether \(\frac{3}{5}\) is less than \(\frac{1}{2}\), greater than \(\frac{1}{2}\) or equal to \(\frac{1}{2}\), you can place these two fractions on the number line.
The diagram below shows the position of \(\frac{1}{2}\) on the number line. You can see that \(\frac{3}{5}\) is more (greater) than \(\frac{1}{2}\) (therefore \(\frac{3}{5} > \frac{1}{2}\)).
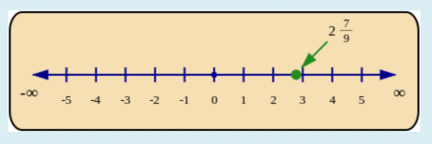
- Improper and mixed numbers (mixed fractions) are placed between two whole numbers. The integer part of the mixed number shows the number after which the fraction is placed on the number line.
The position of \(\frac{25}{9} = 2\frac{7}{9}\) is shown on the number line below.
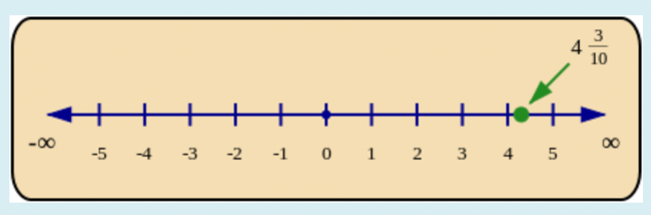
The position of \(4\frac{3}{10}\) is shown on the number line below.
Worked example 13.7: Finding proper fractions on a number line
- What is the fraction at the dot in the following number line?
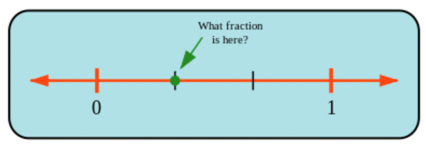
- Is this fraction less than \(\frac{1}{2}\), greater than \(\frac{1}{2}\), or equal to \(\frac{1}{2}\)?
Count the number of parts.
A fraction tells you how many parts there are out of a whole.
The number line in the picture is broken into \(3\) parts between zero and one; these \(3\) pieces make the “whole”. The position of the dot is \(1\) part away from zero. In other words, the position of the dot represents \(1\) part out of \(3\) parts (the whole).
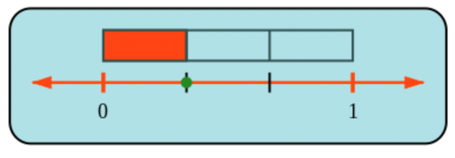
The rectangle above the number line shows how many parts of the whole we need to reach the dot.
That dot represents \(1\) part out of \(3\), which is the fraction \(\frac{1}{3}\).
Compare the fraction to \(\frac{1}{2}\).
Draw a line across the picture to cut the shape in two equal parts:
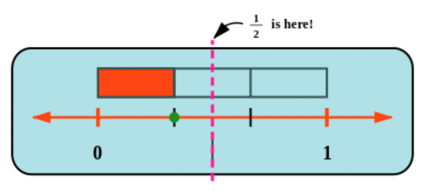
The picture shows the position of \(\frac{1}{2}\) on the number line. You can see that \(\frac{1}{3}\) is smaller than \(\frac{1}{2}\) (therefore \(\frac{1}{3} < \frac{1}{2}\)).
Worked example 13.8: Finding improper fractions and mixed numbers on the number line
Which of the points on the number line below shows the correct location of \(3\frac{2}{9}\)?
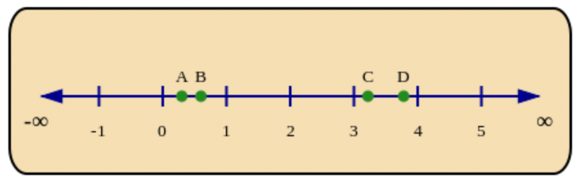
Identify the integer part in the mixed number.
\(3\frac{2}{9}\) is a mixed number. Mixed numbers have an integer part and a fraction part (which must be a proper fraction).
\(3\frac{2}{9}\) has the same meaning as both “\(3 + \frac{2}{9}\)” and “three and two ninths”.
Locate the fraction on the number line.
To find it on the number line, start at 3 on the number line and then add the fraction \(\frac{2}{9}\). That means that \(3\frac{2}{9}\) must be between \(3\) and \(4\).
Now compare the fraction part of the number to \(\frac{1}{2}\): is it more or less than a half? \(\frac{2}{9}\) is less than a half, which means \(3\frac{2}{9}\) must be less than halfway from \(3\) to \(4\).
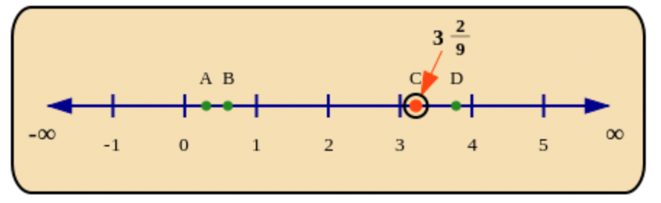
The point that agrees with all of this information is Point C.