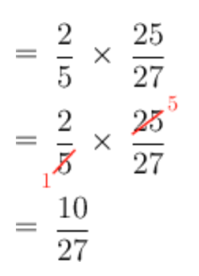13.3 Calculations using fractions
Ordering fractions
Ordering or comparing fractions is easier to do if all the fractions have the same denominator. We will use the concept of equivalent fractions and the lowest common multiple in this context.
Worked example 13.9: Ordering fractions
List the fractions \(\frac{5}{9}\); \(\frac{2}{3}\); \(\frac{4}{7}\) in ascending order.
Find the lowest common multiple of the denominators.
Multiples of \(9\): \(9\); \(18\); \(27\); \(36\); \(45\); \(54\); \(\mathbf{63}\); … \(9 \times 7 = 63\)
Multiples of \(3\): \(3\); \(6\); \(9\); \(12\); \(15\); \(18\); …; \(\mathbf{63}\); … \(3 \times 21 = 63\)
Multiples of \(7\): \(7\); \(14\); \(21\); \(28\); \(35\); …; \(\mathbf{63}\); … \(7 \times 9 = 63\)
The common denominator is \(63\).
Find the equivalent fractions.
\[\frac{5}{9} = \frac{5 \times 7}{9 \times 7} = \frac{35}{63}\] \[\frac{2}{3} = \frac{2 \times 21}{3 \times 21} = \frac{42}{63}\] \[\frac{4}{7} = \frac{4 \times 9}{7 \times 9} = \frac{36}{63}\]List the fractions in ascending order.
Now that the denominators are the same, we can order the numerators: \(35\); \(36\); \(42\).
Therefore, in ascending order, the fractions are: \(\frac{35}{63};\frac{36}{63};\frac{42}{63}\).
Finally, getting back to the given fractions, the fractions listed in ascending order are: \(\frac{5}{9};\frac{4}{7};\frac{2}{3}\).
Worked example 13.10: Ordering fractions
Order the following fractions from smallest to biggest, without using a calculator.
\[\frac{7}{10};\frac{26}{35};\frac{5}{7}\]Find the lowest common denominator.
The lowest common denominator is the smallest number that is a multiple of all the denominators.
Multiples of \(10\): \(10\); \(20\); \(30\); \(40\); …; \(70\); …
Multiples of \(35\): \(35\); \(70\); \(105\); \(140\); …
Multiples of \(7\): \(7\); \(14\); \(21\); \(28\); …; \(70\); …
Therefore, the lowest common denominator is \(70\).
Convert the fractions to fractions that have the lowest common denominator (LCD).
From Step \(1\), we know that the LCD is \(70\). So, we must convert the fractions to equivalent fractions with a denominator of \(70\).
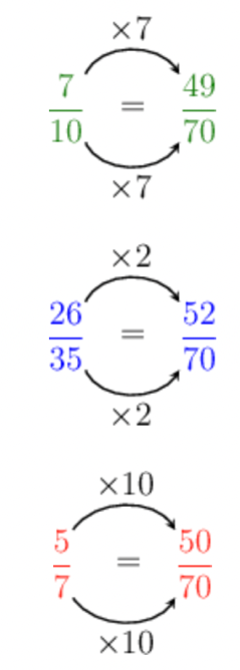
Order the fractions.
Now that the fractions have the same denominator, we only need to look at their numerators.
\[\frac{49}{70} < \frac{50}{70} < \frac{52}{70}\]Therefore, the original fractions ordered from smallest to biggest are:
\[\frac{7}{10};\frac{5}{7};\frac{26}{35}\]Addition and subtraction
To add (or subtract) fractions:
- Make sure that they have the same denominators. Convert the fractions to equivalent fractions with the same denominators using the lowest common denominator (LCD), if necessary.
- Add (or subtract) the numerators.
Worked example 13.11: Adding fractions
Evaluate the following sum without using a calculator:
\[\frac{1}{8} + \frac{5}{12}\]Find the LCD for the fractions and rewrite the sum with equivalent fractions.
The first thing to do is to find the LCD for the fractions \(\frac{1}{8}\) and \(\frac{5}{12}\).
In this case, the LCD is \(24\), so to add the fractions, both of them must have \(24\) as their denominators.
We must rewrite both of the fractions to get this denominator, and we can do this using equivalent fractions.
\[\frac{1}{8} \times \left( \frac{3}{3} \right) + \frac{5}{12} \times \left( \frac{2}{2} \right) = \frac{3}{24} + \frac{10}{24}\]So \(\frac{1}{8} + \frac{5}{12}\) is the same expression as \(\frac{3}{24} + \frac{10}{24}\).
Evaluate the answer and simplify if necessary.
Now we can add the fractions \(\frac{3}{24}\) and \(\frac{10}{24}\). Remember that a fraction shows how many parts in a whole. The first fraction here represents \(3\) out of \(24\), while the second fraction represents \(10\) out of \(24\). If you add the \(10\) to the \(3\), you will get a total of \(13\) out of \(24\).
We can view this sum as a picture. Notice that each of the circles on the left have equally sized pieces: this is what happens when we write the fractions with the same denominators!
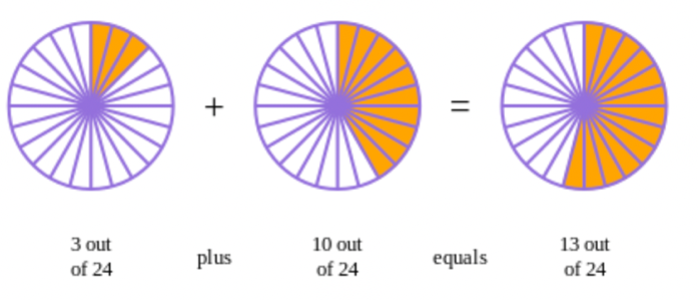
The picture shows that the sum works out to be \(\frac{13}{24}\). Remember that you should always see if the answer can be simplified. In this case, though, it cannot be reduced any more: \(\frac{13}{24}\) is already as simple as possible.
Therefore, the answer for \(\frac{1}{8} + \frac{5}{12}\) is \(\frac{13}{24}\).
Worked example 13.12: Adding fractions
Find the sum of the following fractions:
\[\frac{5}{6} + \frac{23}{24}\]Find the lowest common denominator.
The lowest common denominator (LCD) is the smallest number that is a multiple of all the denominators.
Multiples of \(6\): \(6\); \(12\); \(18\); \(24\); …
Multiples of \(24\): \(24\); \(48\); \(72\); \(96\); …
Therefore, the LCD is \(24\).
Find the equivalent fractions.
Convert the fractions to equivalent fractions using the LCD as the denominator.
\[\frac{5}{6} = \frac{5 \times 4}{6 \times 4} = \frac{20}{24}\]\(\frac{23}{24}\) is already expressed as a numerator over the LCD.
Add the fractions:
\[\begin{align} \frac{5}{6} + \frac{23}{24} &= \frac{20}{24} + \frac{23}{24} \\ &= \frac{20 + 23}{24} \\ &= \frac{43}{24} \end{align}\]\(\frac{43}{24}\) is an improper fraction. You can convert this fraction into a mixed number, so that your answer looks neater. Remember that, to do this, you turn the fraction into a division problem.
\(\frac{43}{24} = 43 \div 24 = 1\frac{19}{24}\).
Worked example 13.13: Subtracting fractions
Evaluate the following difference without using a calculator:
\[\frac{7}{15} - \frac{1}{10}\]Find the LCD for the fractions and rewrite the expression with equivalent fractions.
The first thing to do is to find the LCD for the fractions \(\frac{7}{15}\) and \(\frac{1}{10}\).
In this case, the LCD is \(30\), so to subtract the fractions, we must rewrite both to have \(30\) as their denominators. We can do this using equivalent fractions.
\[\frac{7}{15} \times \left( \frac{2}{2} \right) - \frac{1}{10} \times \left( \frac{3}{3} \right) = \frac{14}{30} - \frac{3}{30}\]\(\frac{7}{15} - \frac{1}{10}\) is the same expression as \(\frac{14}{30} - \frac{3}{30}\).
Evaluate the answer and simplify, if necessary.
Now we can subtract the fractions:
\[\frac{14}{30} - \frac{3}{30}\]Remember that a fraction shows how many parts of a whole. The first fraction here represents \(14\) out of \(30\), while the second fraction represents \(3\) out of \(30\). If you subtract the \(3\) from the \(14\), there will be \(11\) out of \(30\) remaining.
Again, we can view this difference using a diagram. Notice that each of the circles on the left have equally sized pieces: this is what happens when we write the fractions with the same denominators.
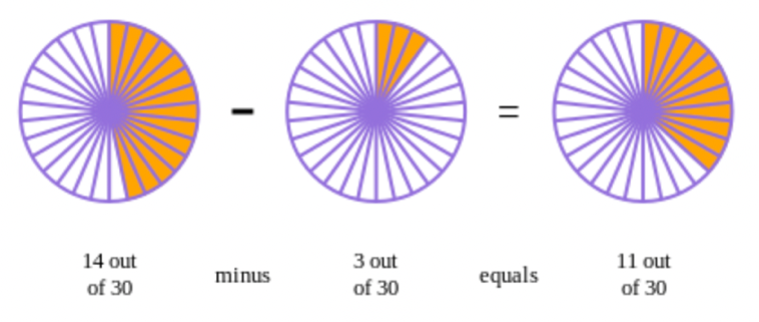
The picture shows that the difference works out to be \(\frac{11}{30}\). Remember that you should always check to see if the answer can be simplified. In this case, though, it cannot be reduced any more: \(\frac{11}{30}\) is already as simple as possible.
Therefore, \(\frac{7}{15} - \frac{1}{10} = \frac{11}{30}\).
Worked example 13.14: Subtracting fractions
Calculate the difference:
\[\frac{14}{13} - \frac{1}{26}\]Find the lowest common denominator.
Multiples of \(13\): \(13\); \(26\); \(39\); \(52\); …
Multiples of \(26\): \(26\); \(52\); \(78\); \(104\); …
The LCD is \(26\).
Find the equivalent fractions.
Convert the fractions to equivalent fractions over the LCD:
\[\frac{14}{13} = \frac{14 \times 2}{13 \times 2} = \frac{28}{26}\]\(\frac{1}{26}\) is already expressed as a numerator over the LCD.
Subtract the fractions:
\[\begin{align} \frac{14}{13} - \frac{1}{26} &= \frac{28}{26} - \frac{1}{26} \\ &= \frac{28 - 1}{26} \\ &= \frac{27}{26} \end{align}\]The answer can be given as a mixed number: \(\frac{27}{26} = 27 \div 26 = 1\frac{1}{26}\).
When subtracting fractions from whole numbers, remember that any whole number can be represented as a fraction over \(1\). For example, \(5 = \frac{5}{1}\) and \(12 = \frac{12}{1}\).
Worked example 13.15: Calculating with fractions and whole numbers
Calculate the following, without using a calculator:
\[4 - \frac{2}{5}\]Change the whole number to a fraction and then find the LCD.
\[\begin{align} 4 - \frac{2}{5} &= \frac{4}{1} - \frac{2}{5} \\ &= \frac{4 \times 5}{1 \times 5} - \frac{2}{5} \\ &= \frac{20}{5} - \frac{2}{5} \\ &= \frac{20 - 2}{5} \\ &= \frac{18}{5} \end{align}\]Convert to a mixed number.
Turning this into a division problem gives \(18 \div 5\).
\(5\) goes into \(18\) \(3\) times with a remainder of \(3\), therefore the final answer is:
\[3\frac{3}{5}\]Multiplication of common fractions, including mixed numbers
Multiplying fractions follows this rule:
\[\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\]To multiply fractions:
- Cross cancel any common factors. (This is not strictly necessary, but it will make your life easier.)
- Multiply the numerators, and then multiply the denominators.
“Cross cancelling” is a very nice way to make multiplying fractions easier. You can cross cancel when you multiply fractions if there is a common factor between the numerator of one fraction and the denominator of another fraction. If there are no common factors, then you cannot cross cancel.
For example, in the multiplication expression, \(\frac{10}{7} \times \frac{11}{4}\), we can cross cancel the numerator \(10\) and the denominator \(4\) because they have a common factor of \(2\). To find the missing number, we must just divide the common factor of \(2\) into \(10\).
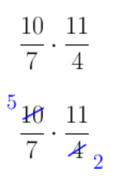
Notice that this is exactly the same as reducing the fraction \(\frac{10}{4}\) to get \(\frac{5}{2}\).
Hint: Remember that a dot between numbers means the same as a \(\times\) sign.
To multiply a whole number by a fraction, convert the whole number to a fraction and follow the same steps.
\[\begin{align} 5 \times \frac{4}{7} &= \frac{5}{1} \times \frac{4}{7} \\ &= \frac{5 \times 4}{1 \times 7} \\ &= \frac{20}{7} \\ &= 2\frac{6}{7} \end{align}\]
Worked example 13.16: Multiplying fractions
Calculate the following, without using a calculator:
\[\frac{8}{7} \times \frac{1}{3}\]Check if it is possible to cross cancel any common factors.
There are no common factors across the numerators and denominators, so we cannot cross cancel. Therefore, we must multiply the numerators and multiply the denominators.
Multiply the numerators and multiply the denominators.
\[\frac{8}{7} \times \frac{1}{3} = \frac{8 \times 1}{7 \times 3} = \frac{8}{21}\]Worked example 13.17: Multiplying fractions
Evaluate the following, without using a calculator:
\[\frac{7}{6} \times \frac{27}{8}\]Cross cancel then multiply.
When you are multiplying fractions, the first thing you should try to do is cross cancel: simplify before you multiply! Look at the numerators and denominators in the fractions: are there any common factors that you can cancel?
Yes, \(3\) goes into both \(6\) and \(27\), so we can cross cancel:
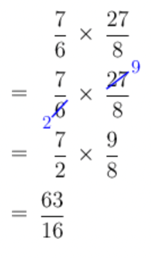
Convert the improper fraction to a mixed number.
Convert the fraction into a division problem.
\[\frac{63}{16} = 63 \div 16\]You can use trial-and-error to find out how many times \(16\) goes into \(63\).
- \(16 × 4 = 64\), so that’s too much. \(16 × 3 = 48\), so the answer is \(3\). \(3\) will be the integer in the mixed number.
- Work out the remainder (what is left over): \(63 - 48 = 15\). \(15\) is the new numerator.
- Keep the denominator the same, so the denominator is still \(16\).
The final answer is:
\[3\frac{15}{16}\]The rules for multiplying with mixed numbers are the same, we just need to add one step – convert mixed numbers to improper fractions.
Worked example 13.18: Multiplying mixed numbers
Calculate the following product:
\[1\frac{4}{5} \times 2\frac{1}{7}\]Convert mixed numbers to improper fractions.
\[1\frac{4}{5} = \frac{(5 \times 1) + 4}{5} = \frac{5 + 4}{5} = \frac{9}{5}\] \[2\frac{1}{7} = \frac{(7 \times 2) + 1}{7} = \frac{14 + 1}{7} = \frac{15}{7}\]Cross cancel.
There are common factors across the numerators and denominators, so we can cross cancel.
\[\frac{9}{5\ \mathbf{\div\ 5}} \times \frac{15\ \mathbf{\div\ 5}}{7} = \frac{9}{1} \times \frac{3}{7}\]Multiply and simplify if possible
\[\frac{9}{1} \times \frac{3}{7} = \frac{9 \times 3}{1 \times 7} = \frac{27}{7} = 3\frac{6}{7}\]Therefore \(1\frac{4}{5} \times 2\frac{1}{7} = 3\frac{6}{7}\)
Worked example 13.19: Multiplying mixed numbers and solving problems
Five friends are sharing a cake, which is cut into \(30\) pieces. The friends eat, on average, \(2\frac{4}{5}\) pieces each. What fraction of the cake is left over?
Determine how many pieces of cake were eaten in total.
We must multiply the number of people by the number of pieces eaten by each person.
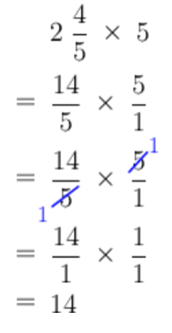
Therefore \(14\) pieces of cake were eaten.
Determine the number of pieces left over.
\[30 - 14 = 16\]Therefore \(16\) pieces of cake are left over.
Determine the fraction of cake left over.
\(16\) out of \(30\) pieces are left over.
\[\frac{16}{30} = \frac{8 \times 2}{15 \times 2} = \frac{8}{15}\]Therefore, \(\frac{8}{15}\) of the cake is left over.
Divide whole numbers and common fractions by common fractions
When dividing fractions, you need to know how to find the reciprocal. The reciprocal of a fraction is another fraction that, when multiplied by the first, gives an answer of \(1\). The second fraction is just the original fraction turned “upside down.” The sign of the number does not change. For example, we need to flip \(\frac{5}{11}\) upside down to get \(\frac{11}{5}\). The two fractions are reciprocals of each other. The reciprocal of \(\frac{5}{11}\) is \(\frac{11}{5}\). The reciprocal of \(\frac{11}{5}\) is \(\frac{5}{11}\):
\[\frac{5}{11} \times \frac{11}{5} = 1\]- reciprocal
- the inverse or opposite of a value; the product of the number and its reciprocal is equal to \(1\)
To divide fractions:
- “Tip and times”: multiply by the reciprocal of the fraction that is the divisor (the second fraction).
- Multiply the fractions as normal.
For example, \(\frac{3}{4} \div \frac{1}{5} = \frac{3}{4} \times \frac{5}{1} = \frac{3\ \times \ 5}{4\ \times \ 1} = \frac{15}{4}\).
Dividing fractions follows this rule, which uses the reciprocal of the second fraction:
\[\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}\]Worked example 13.20: Dividing fractions
Calculate the following, without using a calculator:
\[\frac{5}{7} \div \frac{3}{5}\]Find the reciprocal of the second fraction.
The reciprocal of \(\frac{3}{5}\) is \(\frac{5}{3}\).
Multiply by the reciprocal.
\[\frac{5}{7} \div \frac{3}{5} = \frac{5}{7} \times \frac{5}{3} = \frac{5 \times 5}{7 \times 3} = \frac{25}{21}\]Express the improper fraction as a mixed number.
\[\frac{25}{21} = 25 \div 21 = 1\frac{4}{21}\]Worked example 13.21: Dividing fractions
Calculate the following, without using a calculator:
\[\frac{21}{5} \div \frac{14}{9}\]Find the reciprocal of the second fraction.
The reciprocal of \(\frac{14}{9}\) is \(\frac{9}{14}\), so for this question, the rule gives us this:
\[\begin{align} &\frac{21}{5} \div \frac{14}{9} \\ &\downarrow \\ &\text{rewrite so that you can use multiplication} \\ &\downarrow \\ &\frac{21}{5} \times \frac{9}{14} \end{align}\]Multiply by the reciprocal.
Now we can work out the multiplication problem in the normal way. As always, when multiplying fractions, try to cross cancel.
The working from the beginning to the end should look like this:
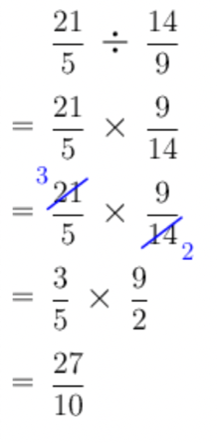
This answer can also be written as a mixed number: \(2\frac{7}{10}\).
When dividing whole numbers by fractions, first convert the whole number to a fraction and then follow the same steps as described above.
For example:
\[5 \div \frac{2}{7} = \frac{5}{1} \div \frac{2}{7} = \frac{5}{1} \times \frac{7}{2} = \frac{35}{2}\]Worked example 13.22: Dividing fractions and whole numbers
Calculate the following, without using a calculator:
\[9 \div \frac{6}{5}\]Write the whole number as a fraction over \(1\) first, then divide the fractions.
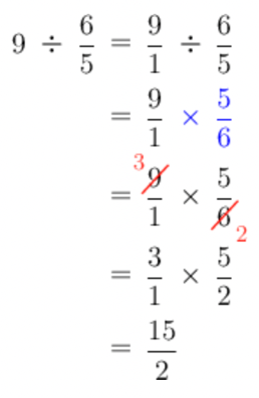
It is best to give your answer as a mixed number: \(7\frac{1}{2}\).
Multiplication and division word problems with fractions
Worked example 13.23: Solving word problems with fractions
Courtney has a pizza that is cut into \(10\) pieces. She cuts each piece into quarters. How many pieces of pizza are there now? (Courtney did not eat any pieces!)
Summarise the given information.
Each of the \(10\) pieces is divided into quarters.
Therefore, the correct number sentence is: \(10 \div \frac{1}{4}\)
We need to find the new number of pieces
Work out the answer.
Calculate the answer to the number sentence in Step \(1\).
\[10 \div \frac{1}{4} = 10 \times \frac{4}{1} = 40\]There are \(40\) pieces now.
Worked example 13.24: Solving word problems with fractions
Lubanzi has \(\frac{1}{4}\) of a cake. He eats \(\frac{3}{5}\) of what he has. What fraction of the whole cake did he eat?
Multiply the fractions to find a fraction of another.
Lubanzi eats \(\frac{3}{5}\) of \(\frac{1}{4}\) of a cake.
\[\frac{3}{5}\text{ of }\frac{1}{4}\ = \frac{3}{5} \times \frac{1}{4} = \frac{3}{20}\]Therefore, Lubanzi ate \(\frac{3}{20}\) of the cake.
Worked example 13.25: Solving word problems with fractions
Seven friends are sharing a cake, which is cut into \(28\) pieces. The friends eat, on average, \(1\frac{6}{7}\) pieces each. What fraction of the cake is left over?
Determine how many pieces of cake the \(7\) friends eat in total.
We must multiply the number of people by the number of pieces eaten by each person.
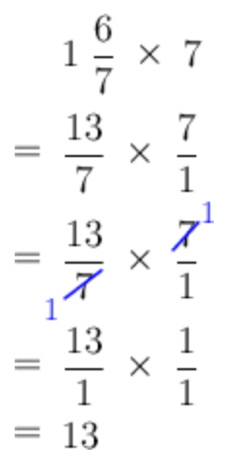
Therefore \(13\) pieces of cake were eaten.
Determine the number of pieces left over.
\[28 - 13 = 15\]Therefore \(15\) pieces of cake are left over.
Determine the fraction of cake left over.
\(15\) out of \(28\) pieces are left over.
Therefore \(\frac{15}{28}\) of the cake is left over.
Worked example 13.26: Solving word problems with fractions
Realeboha is painting a wall with an area of \(5\frac{1}{2}\ \text{m}^{2}\). He has \(4\) cans of paint, each containing \(420\) ml of paint. Each can of paint covers \(1\frac{3}{4}\ \text{m}^{2}\) of the wall.
How many millilitres (ml) of paint are left over after Realeboha has painted the wall (ignoring any potential spillages)?
Summarise the given information.
The area to be painted is \(5\frac{1}{2}\ \text{m}^{2}\)
One can of paint covers \(1\frac{3}{4}\ \text{m}^{2}\)
There are \(4\) cans of paint
\(1\) can = \(450\) ml of paint
We need to find the amount of paint left over.
Choose the correct calculation.
We need to find the number of cans of paint used to cover the whole area.
Divide the area of the wall by the fraction that is covered by each can of paint:
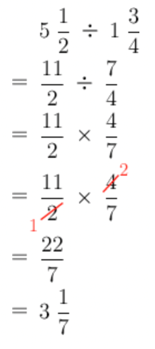
Determine the fraction of cans of paint left over.
Realeboha had \(4\) cans of paint.
\[4 - 3\frac{1}{7} = \frac{4}{1} - \frac{22}{7} = \frac{4 \times 7}{1 \times 7} - \frac{22}{7} = \frac{28}{7} - \frac{22}{7} = \frac{6}{7}\]Find the amount of paint left over.
Multiply the fraction of paint left over by the capacity of the can.
Each can contains \(420\) ml of paint.
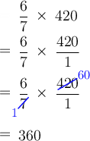
There are \(360\) ml of paint left over.
Calculate the squares, cubes, square roots and cube roots of common fractions
When finding a square of a fraction, start by writing out the fraction two times: that is what the exponent tells you to do!
For example, \(\left( \frac{3}{5} \right)^{2} = \frac{3}{5} \times \frac{3}{5}\). Now this is a multiplication problem:
\[\frac{3}{5} \times \frac{3}{5} = \frac{3 \times 3}{5 \times 5} = \frac{9}{25}\]Worked example 13.27: Finding squares of fractions
Determine the value of each of the following expressions:
\(\left( \frac{9}{8} \right)^{2}\); \(- \left( \frac{9}{8} \right)^{2}\); \(\left( - \frac{9}{8} \right)^{2}\)
Calculate \(\left( \frac{9}{8} \right)^{2}\).
Squared means multiply the fraction by itself.
\[\left( \frac{9}{8} \right)^{2} = \frac{9}{8} \times \frac{9}{8} = \frac{9 \times 9}{8 \times 8} = \frac{81}{64}\]Calculate \(- \left( \frac{9}{8} \right)^{2}\).
It is important to note that the negative sign in front of the brackets will not be squared. The exponent is only “talking” to what is inside the brackets – the exponent is not talking to the negative sign outside the brackets.
\[- \left( \frac{9}{8} \right)^{2} = - \left( \frac{9}{8} \times \frac{9}{8} \right) = - \frac{9 \times 9}{8 \times 8} = - \frac{81}{64}\]Calculate \(\left( - \frac{9}{8} \right)^{2}\).
The exponent tells us to multiply everything inside the brackets by itself. This includes the negative sign. This means that there are two negative signs in the expression.
\[\left( - \frac{9}{8} \right)^{2} = \left( - \frac{9}{8} \right) \times \left( - \frac{9}{8} \right) = + \frac{9 \times 9}{8 \times 8} = \frac{81}{64}\]To take a square root of a fraction, take a square root of the numerator and a square root of the denominator. For example, \(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\).
We can only find the square root of a single term. Therefore, if there is more than one expression, we must simplify the expression within the square root first.
Worked example 13.28: Finding square roots of fractions
Calculate the following, without using a calculator:
\[\sqrt{\frac{7}{2} + \frac{25}{16}}\]Simplify the expression within the square root.
Remember, we add fractions with the same denominators. So, convert \(\frac{7}{2}\) to an equivalent fraction with denominator \(16\) (LCD of \(2\) and \(16\)).
\[\frac{7}{2} = \frac{7}{2} \times \frac{8}{8} = \frac{7 \times 8}{2 \times 8} = \frac{56}{16}\]
We need to add the fractions first:
\[\frac{7}{2} + \frac{25}{16} = \frac{56}{16} + \frac{25}{16} = \frac{81}{16}\]Find the square root.
\[\sqrt{\frac{7}{2} + \frac{25}{16}} = \sqrt{\frac{81}{16}} = \frac{\sqrt{81}}{\sqrt{16}} = \frac{9}{4}\]Just like with squares, to find the cube of a fraction you can begin by multiplying a fraction by itself twice.
For example, \(\left( \frac{2}{3} \right)^{3} = \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} = \frac{2\ \times \ 2\ \times \ 2}{3\ \times \ 3\ \times \ 3} = \frac{8}{27}\).
Another way of doing it is to cube the numerator and to cube the denominator:
\[\left( \frac{2}{3} \right)^{3} = \frac{2^{3}}{3^{3}} = \frac{8}{27}\]Worked example 13.29: Working with cubes in fractions
Calculate the following, without using a calculator:
\[\frac{(9 - 4)^{3}}{6}\]Carry out the calculation.
Hint: Subtract the numbers in the numerator before cubing.
\[\frac{(9 - 4)^{3}}{6} = \frac{(5)^{3}}{6} = \frac{125}{6}\]Convert to a mixed number.
Convert the improper fraction \(\frac{125}{6}\) to a mixed number.
\[\frac{125}{6} = 125 \div 6 = 20\frac{5}{6}\]In this question, only the numerator is cubed, so be careful not to cube the denominator. If the question looked like this: \(\left( \frac{9 - 4}{6} \right)^{3}\) then you would need to cube both the numerator and the denominator.
\[\left( \frac{9 - 4}{6} \right)^{3} = \frac{(9 - 4)^{3}}{6^{3}} = \frac{5^{3}}{6^{3}} = \frac{125}{216}\]
When finding the cube root of a fraction, we must cube root the numerator, and cube root the denominator.
Worked example 13.30: Working with cube roots of fractions
Calculate the following, without using a calculator:
\[\sqrt[3]{\frac{8}{125}} \div \frac{27}{25}\]Simplify the cube root.
There is only one term in this expression. Within a term, we always simplify exponents and roots first. So simplify the cube root first:
\[\sqrt[3]{\frac{8}{125}} = \frac{\sqrt[3]{8}}{\sqrt[3]{125}} = \frac{2}{5}\]Check:
\[\left( \frac{2}{5} \right)^{3} = \left( \frac{2}{5} \right) \times \left( \frac{2}{5} \right) \times \left( \frac{2}{5} \right) = \frac{8}{125}\] \[\sqrt[3]{\frac{8}{125}} = \frac{2}{5}\]Divide.
\[\frac{2}{5} \div \frac{27}{25} = \frac{2}{5} \times \frac{25}{27}\]Cross cancel: \(25 \div 5 = 5\) and \(5 \div 5 = 1\)