11.4 Similar and congruent shapes
Congruent shapes
Two shapes can be described as congruent if they are exactly the same in size and shape. Their position and orientation can be different, but the shape and the size must be identical. In other words, the two shapes should be able to fit on top of each other perfectly.
For two shapes to be congruent, their corresponding angles must be equal and their corresponding sides must be the same length. The diagram shows two congruent triangles, \(\triangle ABC\) and \(\triangle DEF\).
Corresponding angles are equal:
- \(\hat{A} = \hat{D} = 78^{\circ}\)
- \(\hat{B} = \hat{E} = 57^{\circ}\)
- \(\hat{C} = \hat{F} = 45^{\circ}\)
Corresponding sides are equal:
- \(AB = DE = 3 \text{ units}\)
- \(BC = EF = 5 \text{ units}\)
- \(CA = FD = 4 \text{ units}\)
We use this symbol (\(\equiv\)) to indicate that two shapes are congruent.
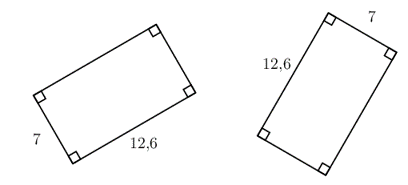
\[\triangle ABC \equiv \triangle DEF\]For two quadrilaterals to be congruent, their corresponding angles must be equal and their corresponding sides must be the same length. The diagram below shows two congruent rectangles. Their corresponding sides are the same length: \(7\) units and \(\text{12,6}\) units, and their corresponding angles are equal: \(90^{\circ}\). Notice that we could rotate one of the rectangles and it would fit exactly on top of the other rectangle.
The diagram below shows a square and a rhombus. Notice that the corresponding sides are the same length, but the corresponding angles are not equal. These two shapes are not congruent.
Corresponding sides must be equal and corresponding angles must be equal.
The diagram below shows two equilateral triangles. The interior angles of both triangles are all \(60^{\circ}\) but their corresponding sides are not equal. The two triangles do not fit exactly on top of each other. These two triangles are not congruent.
Corresponding angles must be equal and corresponding sides must be equal.
Similar shapes
Two shapes are similar if they have the same shape, but they may be different sizes. In other words, two shapes are similar if their corresponding angles are equal (same shape) and their corresponding sides are in the same proportion (different size). The corresponding sides of two shapes are in the same proportion if the length of each side can be multiplied or divided by the same number to make the shape the same size as the other shape. We say that one shape is an enlargement or a reduction of the other shape.
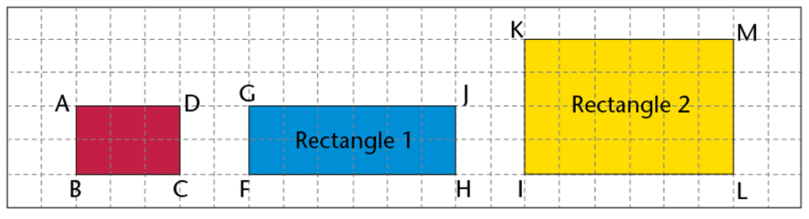
The diagram shows three rectangles. For rectangle \(ABCD\), \(AB = 2 \text{ units}\), \(AD = 3 \text{ units}\) and \(\hat{A} = \hat{B} = \hat{C} = \hat{D} = 90^{\circ}\). Is rectangle 1 similar to rectangle \(ABCD\)? Or is rectangle 2 similar to rectangle \(ABCD\)? We know that the interior angles are all the same (right angles), so we need to find out which rectangle has sides in the same proportion to rectangle \(ABCD\).
We show that the sides are in the same proportion by dividing corresponding sides and obtaining the same value. We know that the opposite sides of a rectangle are equal, so we only need to compare two sides:
Rectangle 1: For rectangle \(GFHJ\), \(GF = 2 \text{ units}\) and \(GJ = 6 \text{ units}\).
- \(\frac{AB}{GF} = \frac{2}{2} = 1\)
- \(\frac{AD}{GJ} = \frac{3}{6} = \frac{1}{2}\)
The proportion of the sides is not the same, so the rectangles are not similar.
Rectangle 2: For rectangle \(KILM\), \(KI = 4 \text{ units}\) and \(KM = 6 \text{ units}\).
- \(\frac{AB}{KI} = \frac{2}{4} = \frac{1}{2}\)
- \(\frac{AD}{KM} = \frac{3}{6} = \frac{1}{2}\)
The sides are in the same proportion, so the rectangles are similar.
We use this symbol, \(|||\), to indicate that two shapes are similar.
Rectangle \(ABCD\) \(|||\) Rectangle \(KILM\)
Worked Example 11.13: Finding similar triangles
Show that \(\triangle ABC ||| \triangle XYZ\).
Show that corresponding angles are equal.
The diagram shows that \(\triangle ABC\) and \(\triangle XYZ\) are right-angled isosceles triangles.
- \(\hat{A} = \hat{X} = 45^{\circ}\)
- \(\hat{B} = \hat{Y} = 90^{\circ}\)
- \(\hat{C} = \hat{Z} = 45^{\circ}\)
For \(\triangle ABC\) and \(\triangle XYZ\), corresponding angles are equal.
Show that corresponding sides are in the same proportion.
We need to show that the sides of the triangles are in the same proportion.
We divide the lengths of corresponding sides:
- \(\frac{AB}{XY} = \frac{2}{4} = \frac{1}{2}\)
- \(\frac{BC}{YZ} = \frac{2}{4} = \frac{1}{2}\)
- \(\frac{CA}{ZX} = \frac{3}{6} = \frac{1}{2}\)
All the sides are in the same proportion, so the triangles are similar.
\[\triangle ABC ||| \triangle XYZ\]