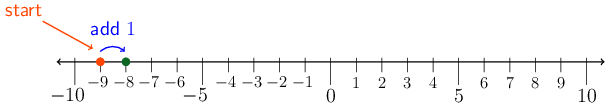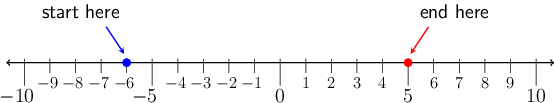2.2 Calculations with integers
Revise addition and subtraction with integers
When calculating with small integers, you can use the number line:
- Count to the left when subtracting a positive number.
- Count to the right when adding a positive number.
Worked example 2.1: Revise addition and
subtraction with integers
Evaluate the following without using a calculator:
\[2 - 8\]
Use a number line.
To subtract \(8\) from \(2\), we must start at \(2\) on the number line and count \(8\) to the left.
Write the calculation.
\[2 - 8 = - 6\]
Worked example 2.2: Revise addition and
subtraction with integers
Evaluate the following without using a calculator:
\[- 9 + 1\]
Use a number line
To add \(1\) to \(−9\), we must start at \(−9\) on the number line and count \(1\) to the
right.
Write the calculation
\[- 9 + 1 = - 8\]
Understanding addition and subtraction with integers
The following statement is true if the unknown number is \(5\):
\(15\) − (a certain number) = \(10\)
Another number will make the following statement true:
\(15\) + (a certain number) = \(10\)
If you add this number, it should have the same effect as to subtract \(5\).
That number is “negative \(5\)”. It has the property that if you add it to another number, the
effect will be the same as when you subtract its positive opposite:
\(15 + ( - 5)\) is equal to \(15 - 5\).
Adding a negative number has the same effect as subtracting a positive number.
For example: \(20 + ( - 15) = 20 - 15 = 5\).
Exercise 2.1 Understanding addition and subtraction of integers
Calculate the following:
-
\(30 + ( - 10)\)
-
\(25 + ( - 15)\)
-
\(10 + ( - 5) - 3\)
-
\(30 + ( - 10) = 30 - 10 = 20\)
-
\(25 + ( - 15) = 25 - 15 = 10\)
- \(10 + ( - 5) - 3 = 10 - 5 - 3 = 5 - 3 = 2\)
or \(10 + ( - 5) - 3 = 10 + ( - 5 - 3) = 10 + ( - 8) = 10 - 8 = 2\)
Worked example 2.3: Addition and subtraction of
integers
Gcina is working with the number line below. She needs to start at the blue dot at \(−6\) and end at
the red dot at \(5\).
What must Gcina do to get from the starting point at \(−6\) to the end point at \(5\)? Write the
number sentence to match this problem.
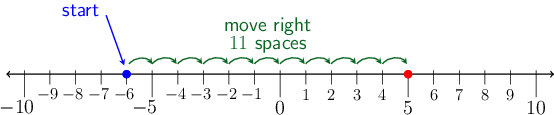
Use a number line.
Moving from the blue dot (\(−6\)) to the red dot (\(5\)) looks like this:
Since the arrows are moving to the right, this is addition.
Adding positive numbers means going to the right, while subtracting positive numbers means
going to the left.
Count the number of spaces between two points.
You can count the number of arrows. This tells us how many units to add to the blue dot to get to the red
dot. In this case there are \(11\) arrows.
The correct final answer is that you need to add \(11\) to \(−6\).
Write the number sentence to match this problem.
The picture tells us how to do this: if we start at \(−6\) and then add \(11\) spaces, we will end up
at \(5\).
The number sentence is:
\[-6 + 11 = 5\]
Multiply with integers
When multiplying with integers, the following rules apply:
- The product of two positive numbers is a positive number, for example \(5 \times 6 = 30\).
- The product of a positive number and a negative number is a negative number, for example \(5 \times ( - 6) =
- 30\).
- The product of a negative number and a positive number is a negative number, for example \(( - 5) \times 6 =
- 30\).
- The product of two negative numbers is a positive number, for example \(( - 5) \times ( - 6) = 30\).
Worked example 2.4: Multiplying integers
Calculate the following without using a calculator: \(- 3 \times ( - 4)\).
Decide on the sign.
When you multiply a negative number and a negative number, you get a positive number. So, the answer will
be positive.
Multiply.
\[- 3 \times ( - 4) = + 12 = 12\]
Worked example 2.5: Multiplying integers
Calculate the following, without using a calculator: \(- 15 \times 2\).
Decide on the sign.
When you multiply a negative number and a positive number, you get a negative number. So, the answer will
be negative.
Multiply.
\[- 15 \times 2 = - 30\]
Worked example 2.6: Multiplying integers
Calculate the following, without using a calculator: \(25 \times ( - 10)\).
Decide on the sign.
When you multiply a positive number and a negative number, you get a negative number. So, the answer will
be negative.
Multiply.
\[25 \times ( - 10) = - 250\]
Divide with integers
When dividing with integers, the following rules apply:
- The quotient of two positive numbers is a positive number, for example \(15 \div 3 = 5\).
- The quotient of a positive number and a negative number is a negative number, for example \(50 \div ( - 5) =
- 10\).
- The quotient of a negative number and a positive number is a negative number, for example \(( - 50) \div 10
= - 5\).
- The quotient of two negative numbers is a positive number, for example \(( - 10) \div ( - 2) = 5\).
Worked example 2.7: Dividing integers
Calculate the following without using a calculator: \(- 30 \div ( - 5)\).
Decide on the sign.
When you divide a negative number and a negative number, you get a positive number. So, the answer will be
positive.
Divide.
\[- 30 \div ( - 5) = + 6 = 6\]
Worked example 2.8: Dividing integers
Calculate the following without using a calculator: \(- 15 \div 3\).
Decide on the sign.
When you divide a negative number and a positive number, you get a negative number. So, the answer will be
negative.
Divide.
\[- 15 \div 3 = - 5\]
Worked example 2.9: Dividing integers
Calculate the following without using a calculator: \(25 \div ( - 5)\).
Decide on the sign.
When you divide a positive number and a negative number, you get a negative number. So, the answer will be
negative.
Divide.
\[25 \div ( - 5) = - 5\]
When it comes to the sign of product or quotient, the rules for multiplication and division with integers
are the same.
When you multiply or divide with negative numbers, there are only two rules you must remember:
- If the numbers have the same signs, then the answer is positive.
- If the numbers have opposite signs, then the answer is negative.
These rules also apply when simplifying fractions. For example, \(\frac{- 49}{7} = - 7\) and \(\frac{-
14}{- 2} = 7\).
Exponents and roots of integers
When finding the square of an integer, we multiply an integer by itself, keeping its sign in mind. For example,
\(12^{2} = 12 \times 12 = 144\) and \(( - 12)^{2} = ( - 12) \times ( - 12) = + 144\).
The square of an integer is always a positive number.
When finding a cube of an integer, we multiply an integer by itself, and by itself again. For example, \(2^{3}
= 2 \times 2 \times 2 = 8\) and \(( - 2)^{3} = ( - 2) \times ( - 2) \times ( - 2) = - 8\).
The cube of an integer is positive if the integer is positive, and negative if the integer is
negative.
Always pay attention to where the minus sign is placed: \(- 5^{2} \neq ( - 5)^{2}\).
\[- 5^{2} = - (5 \times 5) = - 25\]
\[( - 5)^{2} = ( - 5) \times ( - 5) = 25\]
The minus sign of a negative integer raised to a power will always be inside the brackets.
Now have a look at the square roots of integers: \(10^{2}\) is \(100\) and \(( - 10)^{2}\) is also \(100\).
Both \(10\) and (\(−10\)) are called square roots of \(100\). \(10\) is the positive square root of
\(100\) and (\(−10\)) is the negative square root of \(100\):
\(\sqrt{100} = 10\) and \(\sqrt{100} = - 10\)
Cube roots can also be positive or negative numbers. For example,
\(3^{3}\) is \(27\) and \(( - 5)^{3}\) is \(−125\).
\(3\) is called the cube root of \(27\), because \(3^{3} = 27\). So, \(\sqrt[3]{27} = 3\).
\(( - 5)\) is called the cube root of \(−125\) because \(( - 5)^{3} = - 125\). So, \(\sqrt[3]{- 125} = -
5\).
It is possible to take a cube root of a negative integer, but it is not possible to take a square root of a
negative integer.
\(\sqrt[3]{- 8} = - 2\)
but \(\sqrt{- 16}\) is undefined
Worked example 2.10 Calculate cube roots of
integers
Calculate the following without using a calculator:
\[\sqrt[3]{9 + ( - 17)}\]
We can only find the root of a single term. Therefore, we must simplify the expression within the root
first. Simplify under the cube root.
\[9 + ( - 17) = 9 - 17 = 9\textbf{ - 9 - 8 =} - 8\]
Find cube root.
\[\sqrt[3]{- 8} = - 2\]
So,
\[\sqrt[3]{9 + ( - 17)} = \sqrt[3]{- 8} = - 2\]
Worked example 2.11 Calculate cube roots of
integers
Calculate the following without using a calculator:
\[8 - \sqrt[3]{- 64}\]
Find the cube root.
When we take the cube root of a number, we are looking for a number that, when multiplied by itself, and by
itself again, gives the number within the cube root.
\(\sqrt[3]{- 64} = - 4\) because \(( - 4) \times ( - 4) \times ( - 4) = - 64\)
Calculate from left to right.
\[8 - \sqrt[3]{- 64} = 8 - ( - 4) = 8 + 4 = 12\]
Order of operations
Remember that, in any numeric or algebraic sentence, the terms are separated by addition and subtraction
symbols, and joined into one by multiplication symbols, division symbols, and brackets. To simplify or evaluate
an expression, we must:
- separate it into terms
- simplify each term (if needed)
- add or subtract from left to right.
To simplify a term, we must first simplify any parts within brackets. Then we must apply the exponents. If
there are no brackets, then the exponent only applies to the base immediately before it, and we must simplify
the power first.
Worked example 2.12 Evaluate numeric
expressions with integers
Simplify and evaluate: \(- 3 + 2 \times 3^{2}\).
Separate into terms.
There are two terms in this expression: \(( - 3)\) and \((2 \times 3^{2})\).
The first term doesn’t need to be simplified. The second term must be simplified.
Simplify the power.
\[3^{2} = 3 \times 3 = 9\]
Multiply.
\[\left( 2 \times 3^{2} \right) = 2 \times 9 = 18\]
Add the two terms together.
\[- 3 + 2 \times 3^{2} = - 3 + 18 = 15\]
Worked example 2.13 Evaluate numeric
expressions with integers
Calculate the following without using a calculator:
\[6 + (6 - 9) \div 3\]
Separate into terms.
This expression has two terms: \(6\) and \((6 - 9) \div 3\).
We must simplify the second term, and then add from left to right.
Simplify the second term.
The second term has brackets, so we must simplify the expression within the brackets first.
\[(6 - 9) \div 3 = ( - 3) \div 3 = - 1\]
Add the two terms
\[6 + (6 - 9) \div 3 = 6 + ( - 1) = 6 - 1 = 5\]
Worked example 2.14 Evaluate numeric
expressions with integers
Calculate the following without using a calculator:
\[25 \div ( - 5) + 28 \div ( - 2)\]
Separate into terms.
This expression has two terms: \(25 \div ( - 5)\) and \(28 \div ( - 2)\).
We must simplify each term before adding from left to right.
Simplify each term.
\(25 \div ( - 5) = - 5\) and \(28 \div ( - 2) = - 14\)
Add the two terms.
\(25 \div ( - 5) + 28 \div ( - 2)\)
\(= - 5 + ( - 14)\)
\(= - 5 - 14\)
\(= - 19\)