2.3 Counting, ordering and comparing integers
Definition of the integers
The numbers \(1\); \(2\); \(3\); \(4\) etc. are called natural numbers. The natural numbers along with \(0\)
make up the whole numbers. The whole numbers and the negatives of the natural numbers together are called
integers.
The set of integers is defined as follows:
\[\mathbb{Z} = \{\ldots; - 3; - 2; - 1;0;1;2;3;\ldots\}\]
- integers
- the set of positive and negative numbers that can be written without a fractional component, and zero
Here are the important facts about integers.
- The correct symbol for integers is the special letter, \(\mathbb{Z}\).
- The set of integers includes all of the whole numbers as well as the negatives of the natural numbers.
- The set of integers does not include “messy” decimals and fractions like \(\text{4,2}; -
\text{1,5};\frac{1}{2}; - \frac{5}{4}\).
- The following decimals and fractions are elements of the integers, because their result is not a fraction:
\(\text{4,0}; - \text{1,0};\frac{2}{1}; - \frac{10}{2}\).
When we need to describe a number in a set, we use a special symbol, \(\in\), to show that the number
“belongs to” the set or “is an element of” the set.
For example, the statement \(- 4 \text{ } \mathbb{\in Z}\) means that “\(−4\) is an element of the
set of integers”.
You can show this fact on a number line:
Integers on the number line
We can show integers on a number line:
A number line helps us to arrange integers in order. You can see that the distance from the negative number on
the left of \(0\) is the same as the distance to the opposite positive number on the right of \(0\). For
example, there are \(9\) units from \(−9\) to \(0\), and also \(9\) units from \(0\) to \(9\).
The distance between two points on the number line is how far apart the points are, in other words, how many
spaces there are in between them. In the number line above, you can actually just count the spaces between one
point and another.
Exercise 2.2 Find the distance between
points on the number line
The diagram below shows a section of a number line with two labelled points, Point P and Point K. How
far
apart are the points from each other?
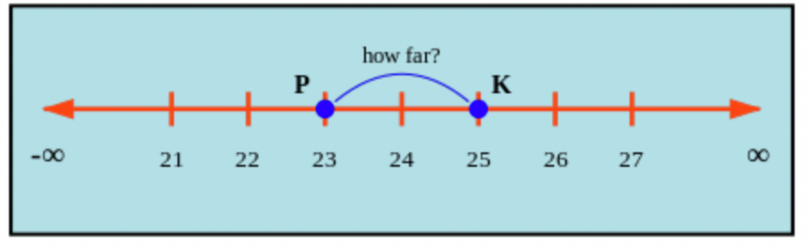
Imagine putting your finger on Point P and just hop your finger over one unit at a time until you reach
Point K. If you add up all of these hops, you can find the total distance between the points.
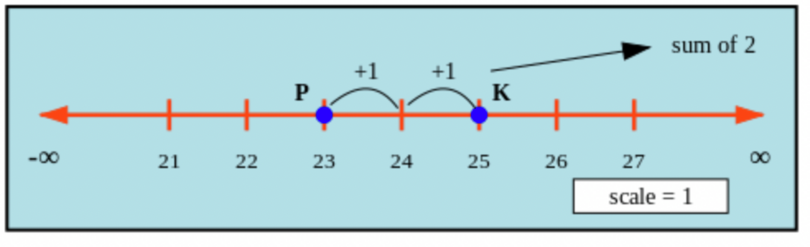
The distance between Point P and Point K is \(2\).
You can count the hops on the number line to get the distance between the points, but there is also a way to
calculate it. You can calculate the distance by subtracting the smaller number from the larger number.
distance = larger number – smaller number
The symbol \(\infty\) on each side of the number line is called the infinity symbol. This means
that the number line will continue in the negative \(( - \infty)\) and in the positive \((\infty)\) direction
infinitely, or forever.
To locate or place a number on a number line:
- Count the number of places from zero. If the number is negative, you count to the left of zero. If the
number is positive, you count to the right of zero.
- First check the scale of the unit marks. You can check this anywhere on the number line.
For example, if you look at \(0\) and \(−5\) on this number line, you can see that there are five spaces
between \(0\) and \(−5\). This means that each unit mark represents a space of \(1\) (or \(1\) unit). If
there had only been a unit mark at \(0\) and \(−5\), and no unit marks in between, then each unit mark
would represent \(5\) units.
- unit mark
- a line that shows where each unit falls on a number line or graph
Worked example 2.15: Finding the number on the
number line
Given the following number line, which number is at point A?
Only some of the unit marks are labelled, so we should first check the scale of the unit marks. We can
check this anywhere on the number line. If we look between \(−5\) and \(−10\), we can see that
there are five spaces between unit marks, so each unit mark represents \(1\) unit.
Count from zero until you reach point A.
Since point A is to the left of zero, we must count backwards, one unit at a time, to get to point A.
Therefore, point A is at \(−4\).
It is also useful to know how to find and place big integers on the number line. For example, the number
\(−105\) is far from \(0\) on the number line, so you would not draw \(105\) unit marks to the left of
\(0\) on the number line. In the number line below, the unit marks represent \(50\) units at a time. You compare
\(−105\) to other numbers on the number line to find its place.
\(−105\) is less than \(−100\). Therefore, point A represents \(−105\).
Counting and ordering integers
We use a number line to help us count or order numbers, too.
For example, to count forwards in \(4\)s, starting at \(−9\), we draw a number line that is long enough
to fit in all the numbers we need.
We must start at \(−9\) and count forwards (to the right) in \(4\)s.
Therefore, the completed list of numbers is \(−9\); \(−5\); \(−1\); \(3\).
Worked example 2.16: Counting integers
Nicky is counting forwards in \(2\)s, starting at \(−5\). She has filled in the first two numbers,
and you must complete the next two.
\(−5\); \(−3\); …; …
Draw a number line.
Place the starting number on your number line.
Count forwards.
We must start at \(−5\) and count forwards (to the right) in \(2\)s.
Therefore, the completed list of numbers is: \(−5\); \(−3\); \(−1\); \(1\).
On a number line, smaller numbers are further to the left, and larger numbers are further to the right.
Therefore, to order the numbers from smallest to largest, we must write them as they appear from left to right
on a number line.
For example, the numbers \(−7\); \(−6\); \(−4\) and \(10\) are in order from smallest to
largest because this is the order in which they appear on a number line.
We use a semi-colon (;) to separate the elements in a list, so when writing numbers in order, we
place a semi-colon between them. For example, \(−5\); \(−1\); \(10\); \(20\).
Remember:
- To place the numbers in \(ascending\) order is to place them from smallest to largest.
- To place the numbers in \(descending\) order is to place them from largest to smallest.
Worked example 2.17: Ordering integers
Place the following integers in ascending order: \(−8\); \(−6\); \(−9\); \(8\).
Place the numbers on a number line.
We need to order the numbers \(−8\); \(−6\); \(−9\) and \(8\). Draw a suitable number
line.
Place the numbers in ascending order.
On the number line, smaller numbers are further to the left, and larger numbers are further to the right.
Therefore, to order the numbers in ascending order, we must write them as they appear from left to right on
the number line: \(−9\); \(−8\); \(−6\); \(8\).
It could get a little trickier when comparing bigger numbers, but you can always let the number line guide you
when you need to order (compare) negative numbers.
For example, you have the numbers \(−96\); \(−99\); \(−82\) and \(−85\), and you must
put them in order from smallest to largest. Draw a number line like this:
Now you can just read off the numbers from left to right. As you go from left to right, the numbers get larger,
so the picture already arranged the numbers in numerical order.
The correct answer is: \(−99\); \(−96\); \(−85\); \(−82\).
It is useful to write this as a big inequality: \(- 99 < - 96 < - 85 < - 82\). If you
read this out loud, it says, “\(−99\) is less than \(−96\) is less than \(−85\) is less
than \(−82\)”.
- numerical order
- when numbers are arranged from smallest to largest














