17.4 Surface area and volume of rectangular prisms
A rectangular prism (also called a cuboid) is a solid with six rectangular faces at right angles to each other.
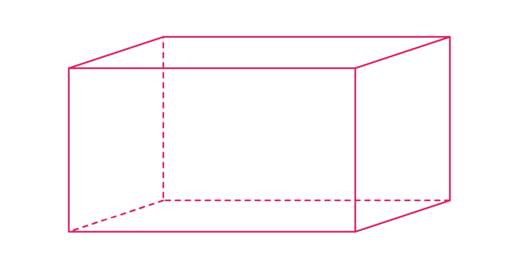
Calculating surface area of a rectangular prism
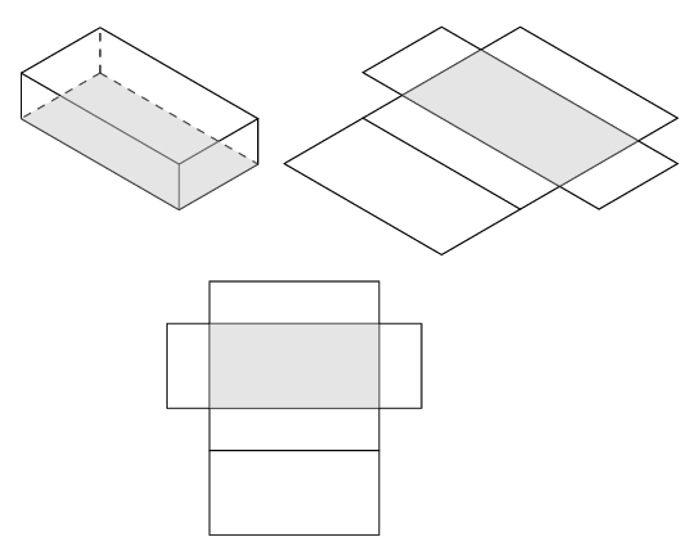
The diagrams below show a cuboid unfolded into a net, which has six rectangular faces. Notice that the rectangular faces are made up of three pairs of identical faces:
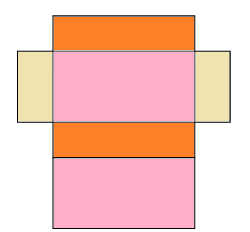
- the vertical side faces are identical (orange rectangles),
- the vertical end faces are identical (yellow rectangles), and
- the horizontal faces are identical (pink rectangles).
Worked Example 17.4: Finding the surface area of a rectangular prism
Find the surface area of the rectangular prism.
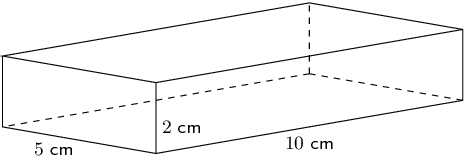
First sketch and label the net of the prism.
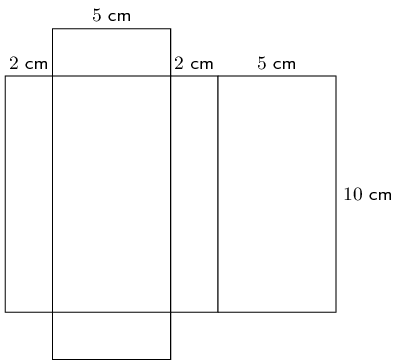
Find the areas of the different rectangles in the net.
\[\begin{align} \text{Area rectangle } 1 &= l \times b \\ &= 2 \times 10 \\ &= 20 \end{align}\] \[\begin{align} \text{Area rectangle } 2 &= l \times b \\ &= 5 \times 10 \\ &= 50 \end{align}\] \[\begin{align} \text{Area rectangle } 3 &= l \times b \\ &= 2 \times 5 \\ &= 10 \end{align}\]Use an alternative approach to finding area of rectangles.
We can also consider the four purple rectangles as one large rectangle. To get the length of the large rectangle, we add up the individual lengths of each rectangle:
\[\begin{align} \text{Length of large rectangle} &= 2 + 5 + 2 + 5 \\ &= 14 \text{ cm} \end{align}\]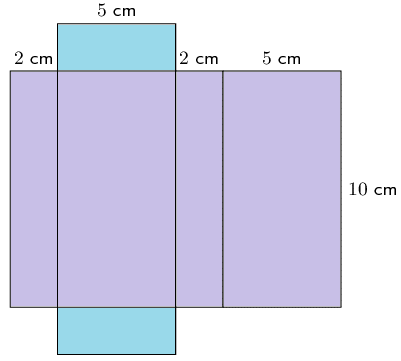
Find the sum of the areas.
Remember to multiply each area by two, as there are two of each type of rectangle.
\[\begin{align} \text{Surface area of cuboid} &= 2(\text{area rectangle }1) + 2(\text{area rectangle }2) + 2(\text{area rectangle }3) \\ &= 2(20) + 2(50) + 2(10) \\ &= 40 + 100 + 20 \\ &= 160 \end{align}\]OR
\[\begin{align} \text{Surface area of cuboid} &= \text{area large rectangle} + 2(\text{area small rectangle}) \\ &= 140 + 2(10) \\ &= 160 \end{align}\]Write the final answer.
The surface area of the rectangular prism is \(160 \text{ cm}^2\).
Calculating volume of a rectangular prism
The volume of a cuboid is calculated by multiplying the area of the base by the height of the cuboid.
\[\text{Volume } = l \times b \times h\]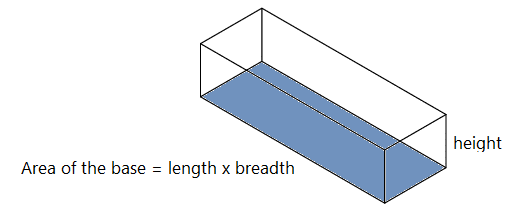
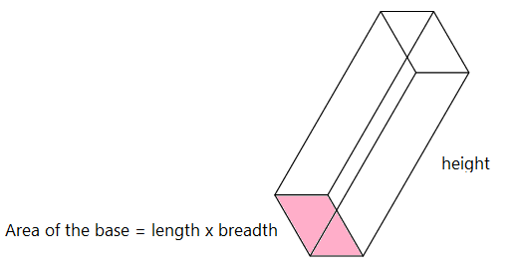
To find the volume of a rectangular prism, we can choose any side as the base of the prism.
Worked Example 17.5: Calculating the volume of a cuboid
The height of the rectangular prism is \(17 \text{ cm}\), the length is \(23 \text{ cm}\), and the breadth is \(5 \text{ cm}\). Calculate the volume of the object.
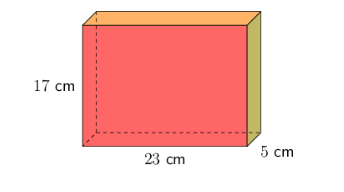
Use the formula for volume of a prism.
\[\begin{align} \text{Volume of prism} &= \text{area of base} \times \text{height} \\ &= (l \times b) \times h \end{align}\]Calculate the volume of the rectangular prism.
\[\begin{align} \text{Volume of prism} &= 23 \times 5 \times 17 \\ &= 1\ 955 \end{align}\]Write the final answer.
Remember to show the correct units in the answer.
Volume of the rectangular prism \(= 1\ 955 \text{ cm}^3\).
Worked Example 17.6: Using volume to find the height of a cuboid
The volume of the rectangular prism is \(1\ 080 \text{ m}^3\). Calculate the value of \(x\).
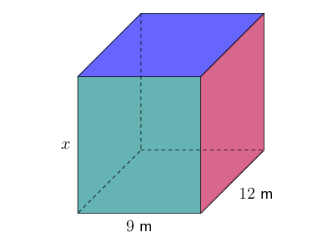
Write the formula for volume of a prism.
\[\begin{align} \text{Volume of prism} &= \text{area of base} \times \text{height} \\ &= (l \times b) \times h \end{align}\]Use the volume of the rectangular prism to find the value of \(x\).
\[\begin{align} \text{Volume of prism} &= 1\ 080 \text{ m}^3 \\ 1\ 080 &= 9 \times 12 \times x \\ 1\ 080 &= 108 \times x \\ \frac{1\ 080}{108} &= \frac{108x}{108} \\ 10 &= x \end{align}\]Write the final answer.
Remember to show the correct units in the answer.
Height of the rectangular prism \(x = 10 \text{ m}\).
