17.5 Surface area and volume of triangular prisms
A triangular prism has two identical triangular bases and three rectangular sides joined at right angles to the bases.
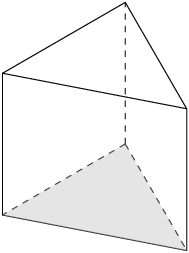
We can calculate the surface area of the prism by finding the area of the triangular faces and the rectangular faces, and then adding them all together.
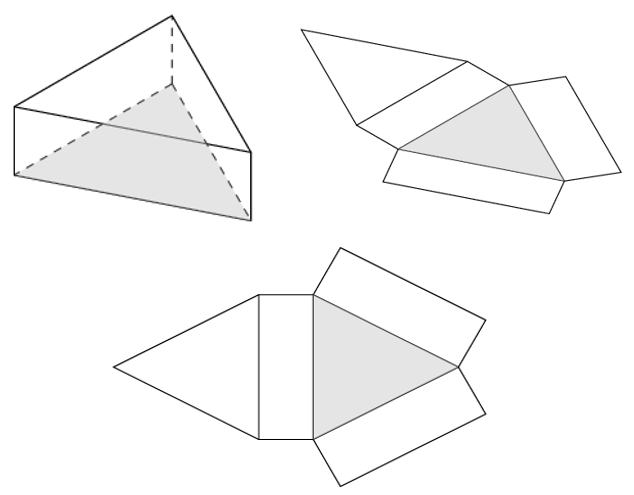
The net of a triangular prism consists of two triangular faces and three rectangular faces.
Worked Example 17.7: Finding the surface area of a triangular prism
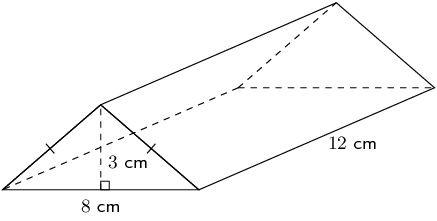
Find the surface area of the triangular prism.
Sketch and label the net of the triangular prism.
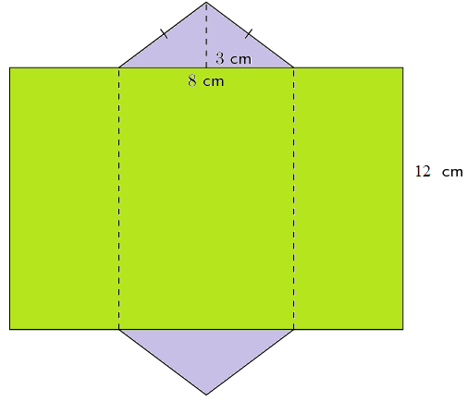
Find the areas of the middle rectangle in the net.
\[\begin{align} \text{Area rectangle} &= l \times b \\ &= 8 \times 12 \\ &= 96 \end{align}\]Use the theorem of Pythagoras to find the length of the hypotenuse.
The theorem of Pythagoras is covered in detail in Chapter 15, but it states that the square of the longest side in a right-angled triangle is equal to the sum of the squares of the other two sides. We use this theorem to work out the length of one side of a right-angled triangle if given the other two sides.
For the two smaller rectangular faces, we know that the breath is \(12 \text{ cm}\) but we do not know the length. The length of a small rectangle is equal to the length of the hypotenuse of one of the right-angled triangles (orange line in diagram below) that is formed by the \(3 \text{ cm}\) height of the triangle.
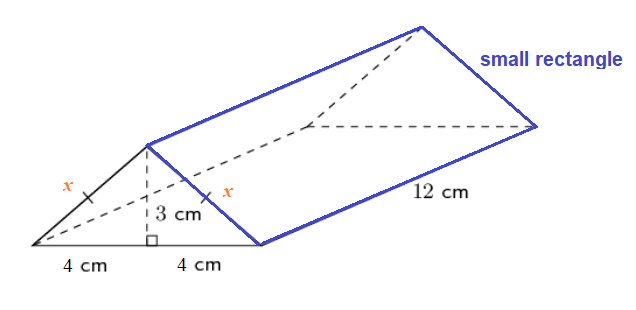
To use the theorem of Pythagoras for one half of the triangular faces:
Let the length of the longest side \(= x\)
\[\begin{align} x^2 &= 4^2 + 3^2 \\ x^2 &= 16 + 9 \\ x^2 &= 25 \\ x &= 5 \end{align}\]The longest side is equal to \(5 \text{ cm}\).
\[\begin{align} \text{Area of small rectangles} &= l \times b \\ &= 5 \times 12 \\ &= 60 \end{align}\]Find the area of the triangular faces.
\[\begin{align} \text{The area of a triangle} &= \frac{1}{2} b \times h \\ &= \frac{1}{2} (8 \times 3) \\ &= 12 \end{align}\]Find the sum of the areas of the faces.
\[\begin{align} \text{Surface area of triangular prism} &= 2(\text{area small rectangle}) + (\text{area middle rectangle}) + 2(\text{area triangle}) \\ &= 2(60) + 96 + 2(12) \\ &= 120 + 96+ 24 \\ &= 240 \end{align}\]Write the final answer.
The surface area of the triangular prism is \(240 \text{ cm}^2\).
Calculating volume of a triangular prism
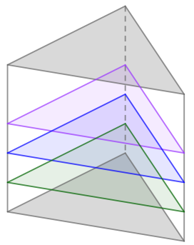
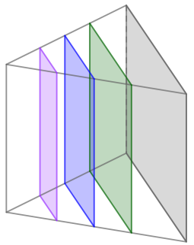
The volume of a triangular prism is calculated by multiplying the area of the triangular base by the height of the prism. To calculate the volume of a triangular prism, we must use the triangular face as the base of the prism so that the cross section of the prism is uniform (in other words, the same shape and area all the way up).
| Base: Triangular face Cross section: Uniform |
Base: Rectangular face Cross section: Not uniform |
 |
 |
Worked Example 17.8: Calculating volume of a triangular prism
Calculate the volume of the prism.
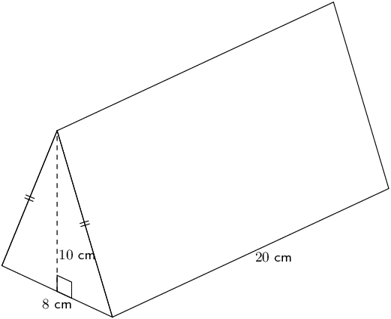
Use the formula for the area of the base.
\[\begin{align} \text{Area of triangle} &= \frac{1}{2}(b \times h) \\ &= \frac{1}{2}(8 \times 10) \\ &= 40 \end{align}\]Calculate the volume of the triangular prism.
\[\begin{align} \text{Volume of prism} &= \text{area of base} \times h \\ &= 40 \times 20 \\ &= 800 \end{align}\]Write the final answer.
Volume of the triangular prism \(= 800 \text{ cm}^3\).
Worked Example 17.9: Using volume to find an unknown length of a triangular prism
The volume of the rectangular prism is \(1\ 650 \text{ cm}^3\). Calculate the value of \(x\). All measurements are given in centimetres.

Write the formula for volume of a triangular prism.
\[\begin{align} \text{Volume of prism} &= \text{area of base} \times \text{height} \\ &= \frac{1}{2}(b \times h) \times h \end{align}\]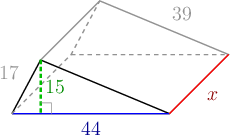
Use the volume of the rectangular prism to find the value of \(x\).
\[\begin{align} \text{Volume of prism} &= 1\ 650 \text{ cm}^3 \\ 1\ 650 &= \frac{1}{2} (44 \times 15) \times x \\ 1\ 650 &= 330x \\ 5 &= x \end{align}\]Write the final answer.
Height of the triangular prism \(x = 5 \text{ cm}\).
