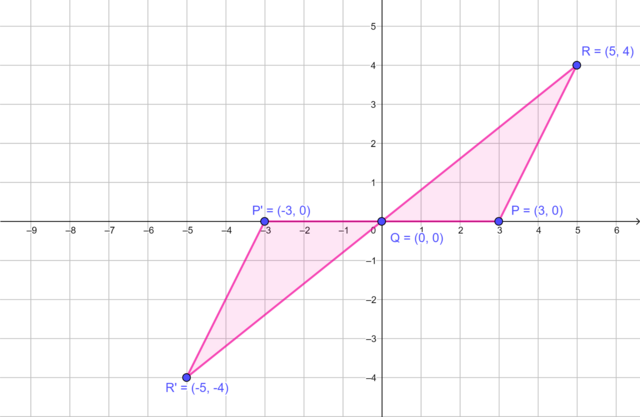
\(\triangle P'Q'R'\), the image of \(\triangle PQR\) rotated by \(180°\) in a clockwise (or anti-clockwise) direction about the origin.
|
Previous
Reflection transformations
|
Next
Enlargement and reduction transformations
|
A rotation is a transformation that rotates or turns an object. A rotation transformation is a rule that has three components:
For example, we can rotate point \(A\) by \(90°\) in a clockwise direction about the origin.
Notice that all three components are included in this transformation statement.
A clockwise direction means turning in the same direction as the hands of a clock. We can also describe clockwise as turning to the right from top to bottom.

An anti-clockwise direction means turning in the opposite direction to the direction of the hands of a clock. We can also describe anti-clockwise as turning to the left from top to bottom.

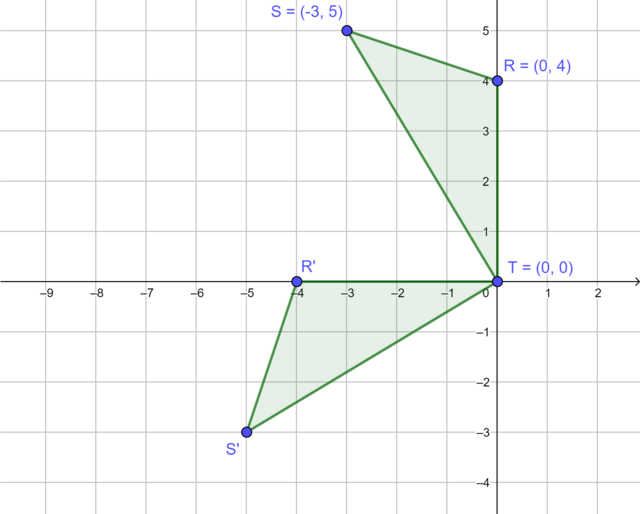
In the diagram, \(\triangle MNP\) is rotated \(180°\) in a clockwise direction about the origin to produce \(\triangle M'N'P'\).
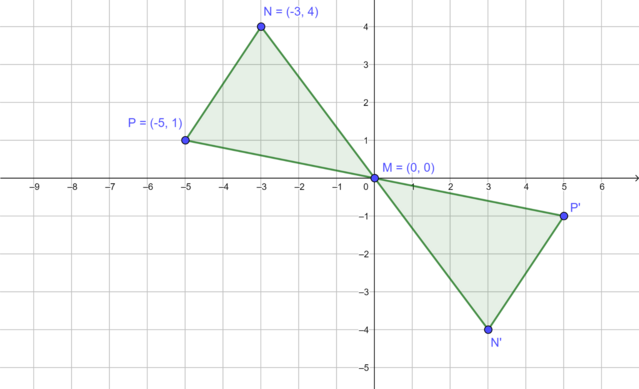
In the diagram, \(\triangle TRS\) is rotated \(90°\) in an anti-clockwise direction about the origin to produce \(\triangle T'R'S'\).
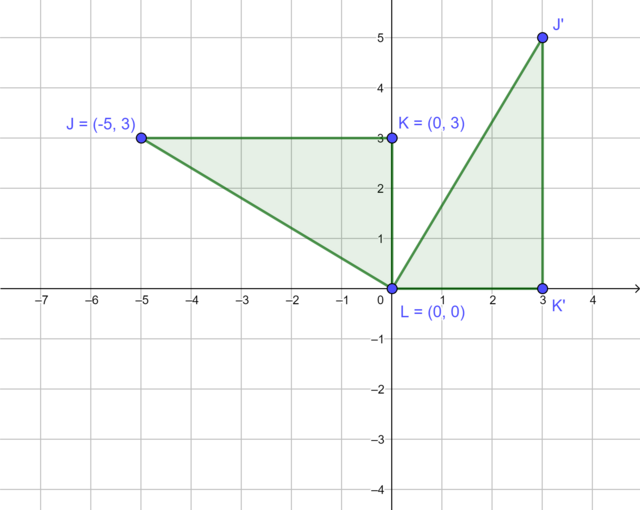
In the diagram, \(\triangle JKL\) is rotated \(90°\) in a clockwise direction about the origin to produce \(\triangle J'K'L'\).
When we rotate an object through a certain angle, every point on the object is rotated through the same number of degrees. The diagram shows that \(\triangle X'Y'Z'\) is the image of \(\triangle XYZ\) rotated by \(90°\) in a clockwise direction about the origin. Notice that every vertex of \(\triangle XYZ\) has been rotated through \(90°\) to produce the corresponding vertex of \(\triangle X'Y'Z'\).
Vertex \(X'\) is the image of vertex \(X\) rotated by \(90°\) in a clockwise direction about the origin.
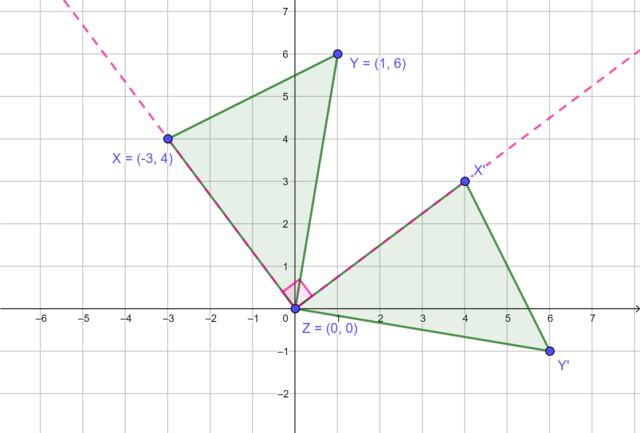
Vertex \(Y'\) is the image of vertex \(Y\) rotated by \(90°\) in a clockwise direction about the origin.
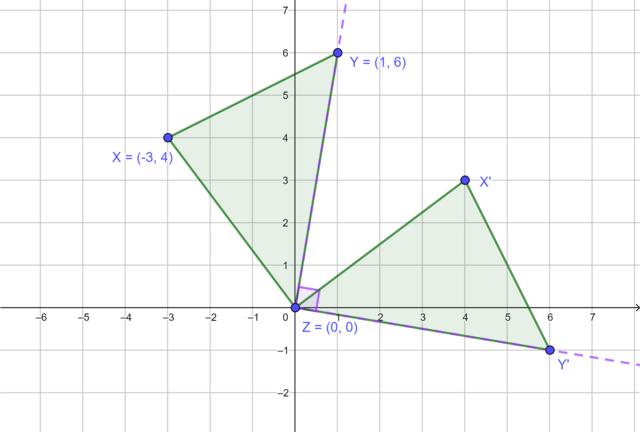
Vertex \(Z\) is on the origin so it stays in the same position.
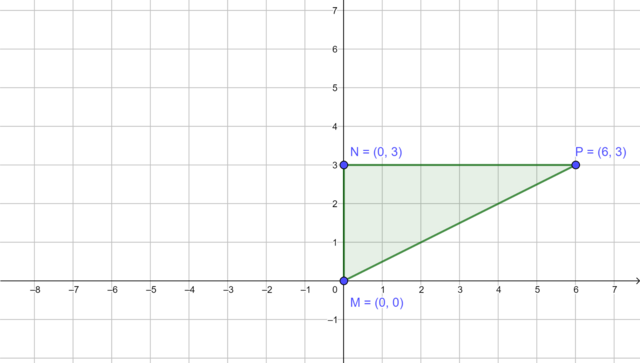
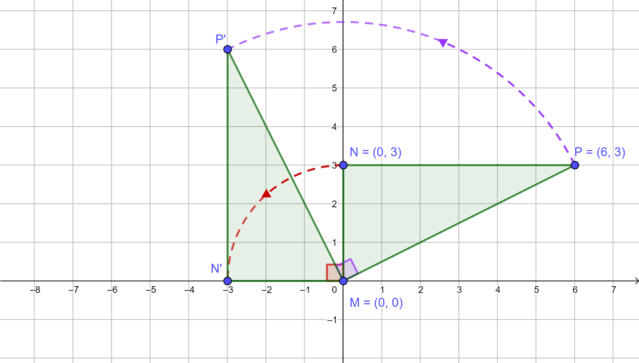
First, we look at the values of the coordinates of the vertices of \(\triangle MNP\) so that we draw the Cartesian plane to an appropriate size. Then, we plot each vertex and draw \(\triangle MNP\). We notice that vertex \(M\) is on the origin.
We rotate each vertex to find its image.
Vertex \(N(0; 3)\) lies on the \(y\)-axis, so after rotating \(90°\) in an anti-clockwise direction about the origin, \(N'(-3; 0)\) lies on the \(x\)-axis.
Vertex \(P(6; 3)\) lies in the first quadrant. After rotating \(90°\) in an anti-clockwise direction about the origin, \(P'(-3; 6)\) lies in the second quadrant.
For each diagram, describe the rotation transformation. Remember to state the angle of rotation, the direction of rotation and the centre of rotation in each case.

\(\triangle P'Q'R'\), the image of \(\triangle PQR\) rotated by \(180°\) in a clockwise (or anti-clockwise) direction about the origin.
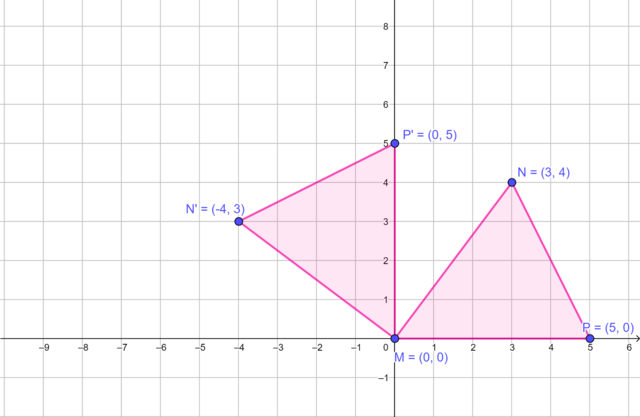
\(\triangle M'N'P'\), the image of \(\triangle MNP\) rotated by \(90°\) in an anti-clockwise direction about the origin.
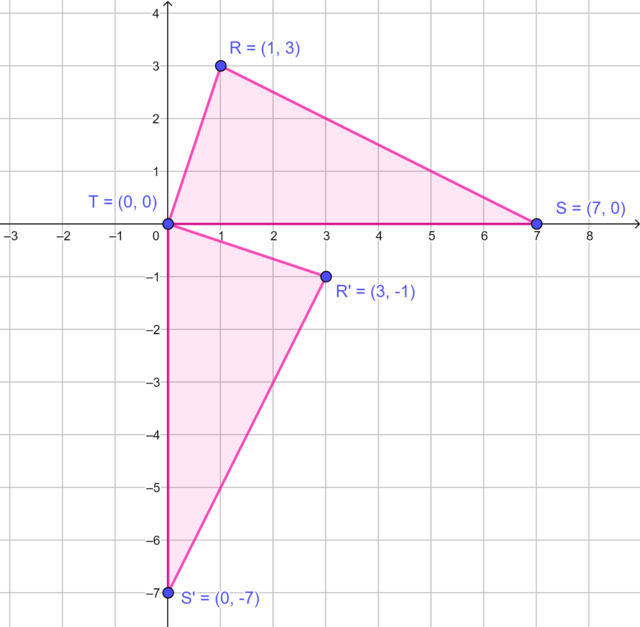
\(\triangle R'S'T'\), the image of \(\triangle RST\) rotated by \(90°\) in a clockwise direction about the origin.
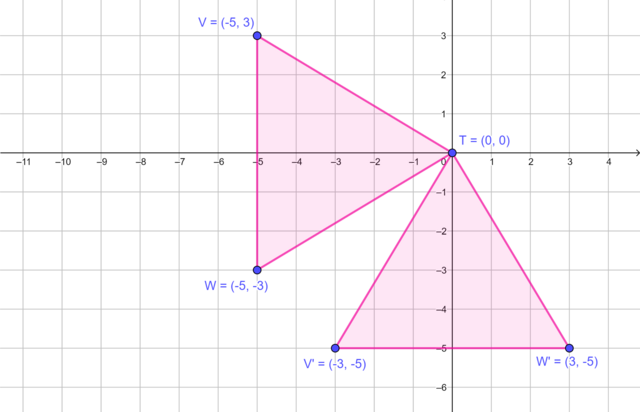
\(\triangle T'V'W'\), the image of \(\triangle TVW\) rotated by \(90°\) in an anti-clockwise direction about the origin.
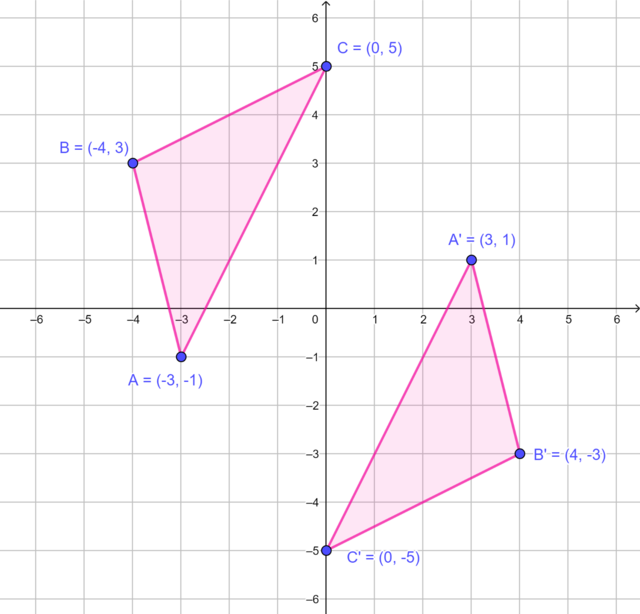
\(\triangle A'B'C'\), the image of \(\triangle ABC\) rotated by \(180°\) in a clockwise (or anti-clockwise) direction about the origin.
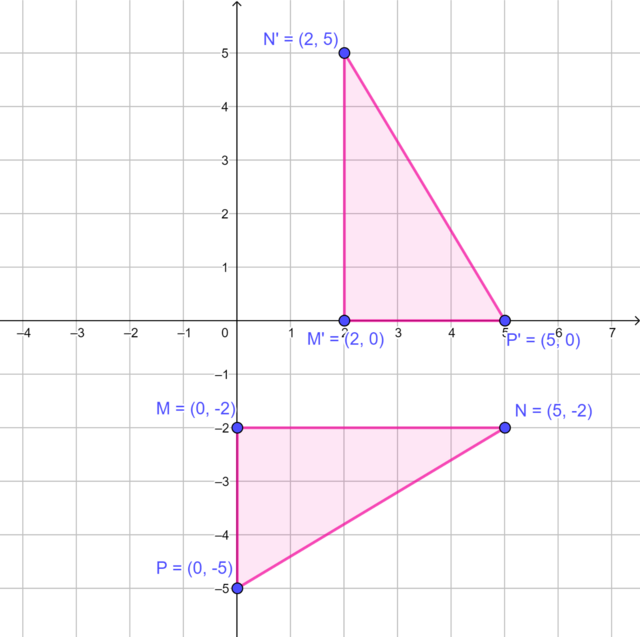
\(\triangle M'N'P'\), the image of \(\triangle MNP\) rotated by \(90°\) in an anti-clockwise direction about the origin.
Complete the following on the Cartesian plane:
Draw \(\triangle KLM\) with vertices \(K(-6; 0)\), \(L(-1; -3) \) and \(M(0; 0)\).
Draw \(\triangle K'L'M'\) the image of \(\triangle KLM\) rotated by \(180°\) in a clockwise direction about the origin.
Triangle \(A\) is the original triangle. Describe the rotation transformation that produces triangle \(B\) and triangle \(C\).
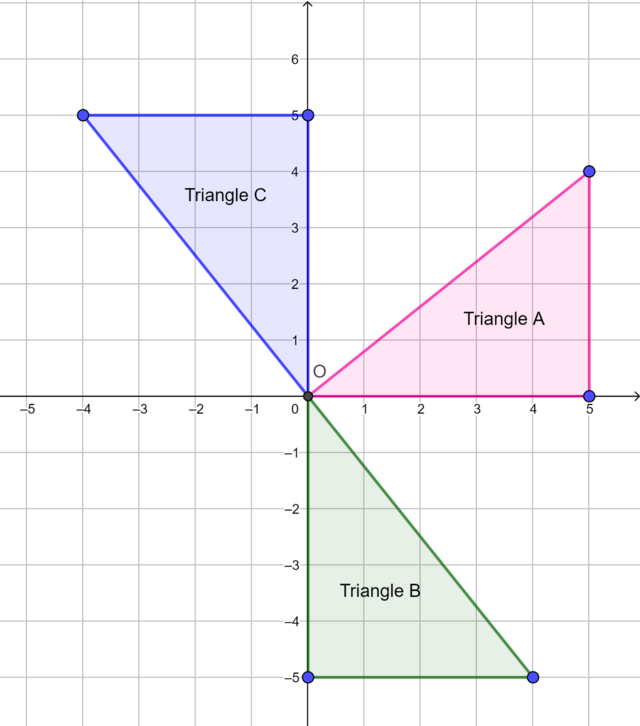
Triangle \(B\) is the image of triangle \(A\) rotated by …
Triangle \(C\) is the image of triangle \(A\) rotated by …
Triangle \(B\) is the image of triangle \(A\) rotated by \(90°\) in a clockwise direction about the origin.
Triangle \(C\) is the image of triangle \(A\) rotated by \(90°\) in an anti-clockwise direction about the origin.
Triangle \(A\) is the original triangle. Describe the rotation transformation that produces triangle \(B\) and triangle \(C\).

Triangle \(B\) is the image of triangle \(A\) rotated by …
Triangle \(C\) is the image of triangle \(A\) rotated by …
Triangle \(B\) is the image of triangle \(A\) rotated by \(90°\) in an anti-clockwise direction about the origin.
Triangle \(C\) is the image of triangle \(A\) rotated by \(180°\) in a clockwise (or anti-clockwise) direction about the origin.
Complete the following on the Cartesian plane:
Draw \(\triangle PQR\) with vertices \(P(5; 0)\), \(Q(0; 0)\) and \(R(4; -3)\).
Draw \(\triangle P'Q'R'\), the image of \(\triangle PQR\) rotated by \(90°\) in a clockwise direction about the origin.
|
Previous
Reflection transformations
|
Table of Contents |
Next
Enlargement and reduction transformations
|