24.5 Reflection transformations
Reflecting a point on the Cartesian plane
We can reflect (flip) a point on the Cartesian plane over a certain line. This line is called the line of reflection or the mirror line. The reflected point is called the mirror image. Any line on the Cartesian plane can be used as a line of reflection. In this section we will transform objects using the \(x\)-axis and \(y\)-axis as lines of reflection.
- line of reflection
- the line that separates a point, a line or an object and its reflected image
- mirror image
- the new position of a point, a line or an object after it has been reflected
Reflecting a point in the \(x\)-axis
In the diagram, point \(P(2; 3)\) is reflected in the \(x\)-axis (\(y=0\)) to produce image \(P'(2; -3)\). We say that \(P'\) is the image of \(P\) under a reflection transformation.
What do you notice about the values of the coordinates of \(P'\)?
What do you notice about the perpendicular distances of \(P\) and \(P'\) to the \(x\)-axis?
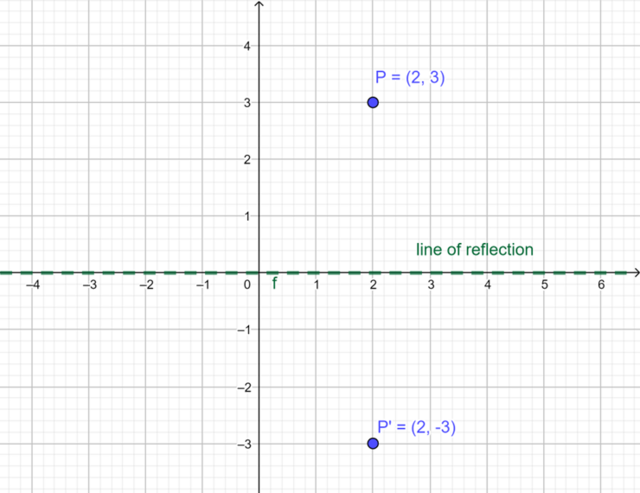
Notice that \(P\) lies in the first quadrant (positive \(x\)-value, positive \(y\)-value) and \(P'\) lies in the fourth quadrant (positive \(x\)-value, negative \(y\)-value).
We can express this reflection transformation in mapping notation as:
\[(x; y) \rightarrow (x; -y)\]Reflecting a point in the \(y\)-axis
We can also reflect a point on the Cartesian plane in the \(y\)-axis, which is the line \(x = 0\). In the diagram, point \(T(2; 3)\) is reflected in the \(y\)-axis to produce image \(T'(-2; 3)\).
What do you notice about the values of the coordinates of \(T\) and \(T'\)?
What do you notice about the perpendicular distances of \(T\) and \(T'\) to the \(y\)-axis?
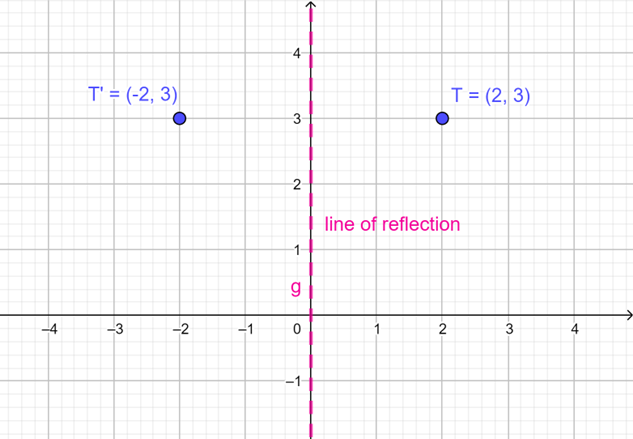
Notice that \(T\) lies in the first quadrant (positive \(x\)-value, positive \(y\)-value) and \(T'\) lies in the second quadrant (negative \(x\)-value, positive \(y\)-value).
We can express this reflection transformation in mapping notation as:
\[(x; y) \rightarrow (-x; y)\]We notice that the point and its image are the same perpendicular distance from the line of reflection. In other words, there is symmetry with respect to the line of reflection. In the diagram, \(T\) is 2 units from the \(y\)-axis and \(T'\) is also 2 units from the \(y\)-axis.
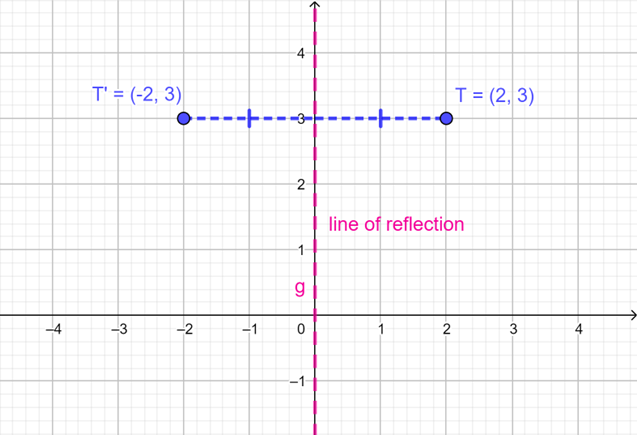
We see that reflecting a point in the \(x\)-axis changes the sign of the \(y\)-coordinate, and reflecting a point in the \(y\)-axis changes the sign of the \(x\)-coordinate.
Reflecting \(P(x; y)\) in the \(x\)-axis produces image \(P'(x; -y)\):
\[(x; y) \rightarrow (x; -y)\]
Reflecting \(T(x; y)\) in the \(y\)-axis produces image \(T'(-x; y)\):
\[(x; y) \rightarrow (-x; y)\]
Worked example 24.4: Reflecting a point on the Cartesian plane
Complete the following:
- Plot \(C(-1; 3)\) on the Cartesian plane.
- Write down the coordinates of \(C'\), the image of \(C(-1; 3)\) reflected in the \(x\)-axis.
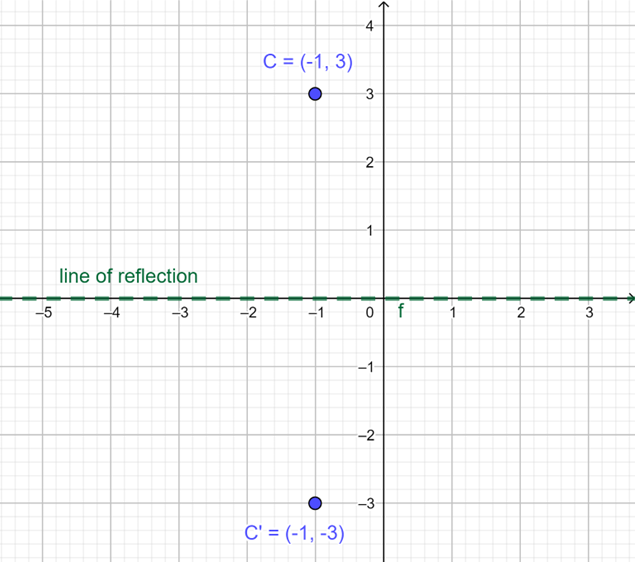
Plot point \(C\) on the Cartesian plane.
We plot the point \(C(-1; 3)\) on the Cartesian plane. Point \(C\) lies in the second quadrant.
Identify the line of reflection.
We need to reflect \(C\) in the \(x\)-axis (that is, in the line \(y = 0\)). We know that by reflecting a point in the \(x\)-axis to get its image, the value of the \(x\)-coordinate stays the same and the value of the \(y\)-coordinate changes its sign.
Plot image \(C'\) on the Cartesian plane.
\(C'\) lies in the third quadrant. The coordinates of the image \(C'\) are \((-1; -3)\).
The perpendicular distance between \(C\) and the \(x\)-axis is 3 units and the perpendicular distance between \(C'\) and the \(x\)-axis is 3 units.
Write the final answer.
\(C'(-1; -3)\).
Reflecting a shape on the Cartesian plane
We can also reflect a shape over a mirror line on the Cartesian plane. In this section, we will transform shapes such as triangles, squares and rectangles using the \(x\)-axis and the \(y\)-axis as lines of reflection.
Reflecting a shape in the \(x\)-axis
The diagram shows \(\triangle PQR\) with vertices \(P(4; 3)\), \(Q(0; 1)\) and \(R(-1; 3)\).
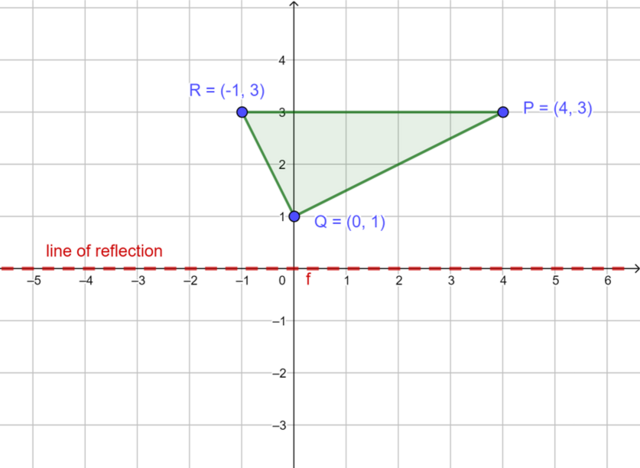
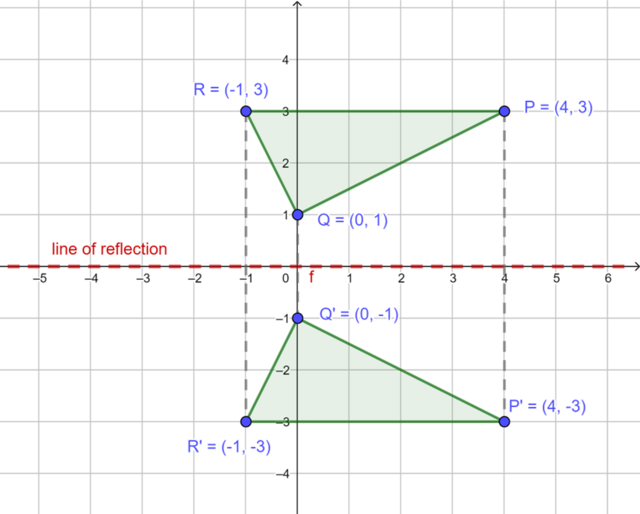
We can reflect \(\triangle PQR\) in the \(x\)-axis (\(y=0\)) to produce the image \(\triangle P'Q'R'\). To find the corresponding coordinates of the image of reflection in the \(x\)-axis, we keep the value of the \(x\)-coordinate the same and change the sign of the \(y\)-coordinate.
We can express this transformation in mapping notation as:
\[(x; y) \rightarrow (x; -y)\]Reflecting \(P(4; 3)\) in the \(x\)-axis produces image \(P'(4; -3)\).
Reflecting \(Q(0; 1)\) in the \(x\)-axis produces image \(Q'(0; -1)\).
Reflecting \(R(-1; 3)\) in the \(x\)-axis produces image \(R'(-1; -3)\).
Reflecting a shape in the \(y\)-axis
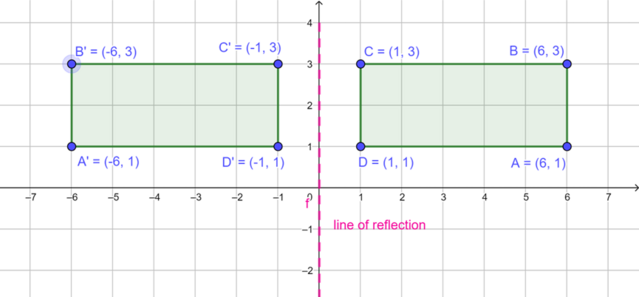
We can also reflect a shape using the \(y\)-axis as the line of reflection. The diagram shows rectangle \(ABCD\) with vertices \(A(6; 1)\), \(B(6; 3)\), \(C(1; 3)\) and \(D(1; 1)\).
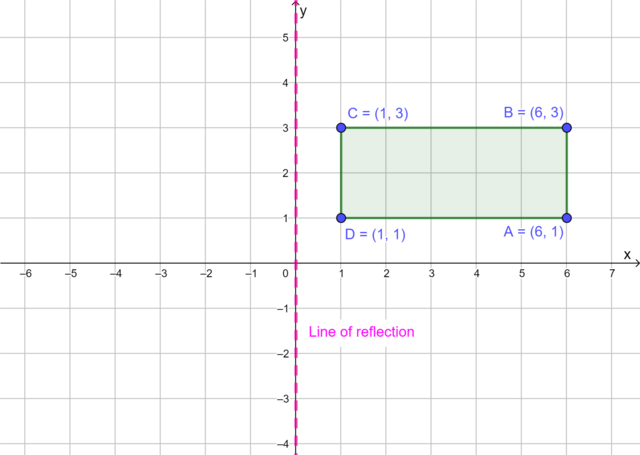
We can reflect rectangle \(ABCD\) in the \(y\)-axis (\(x=0\)) to produce the image \(A'B'C'D'\). To find the corresponding coordinates of the image of reflection in the \(y\)-axis, we change the sign of the \(x\)-coordinate and keep the value of the \(y\)-coordinate the same.
We can express this transformation in mapping notation as:
\[(x; y) \rightarrow (-x; y)\]Reflecting the vertices of rectangle \(ABCD\) in the \(y\)-axis we get:
- the image of \(A(6; 1)\) is \(A'(-6; 1)\)
- the image of \(B(6; 3)\) is \(B'(-6; 3)\)
- the image of \(C(1; 3)\) is \(C'(-1; 3)\)
- the image of \(D(1; 1)\) is \(D'(-1; 1)\)