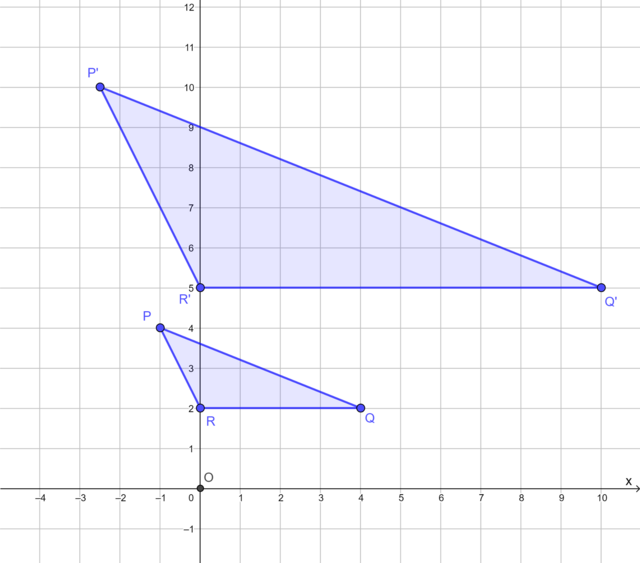
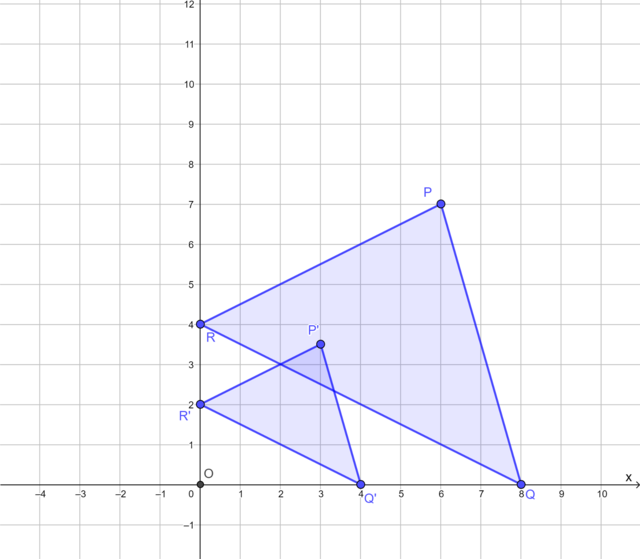
The diagram shows \(\triangle PQR\) and its image \(\triangle P'Q'R'\) under an enlargement transformation with the origin as the centre of enlargement.
24.7 Enlargement and reduction transformations
We can use transformations to change the size of a shape. To make a shape bigger, we use an enlargement transformation. This is sometimes referred to as stretching or expanding a shape. To make a shape smaller, we use a reduction transformation, also referred to as shrinking a shape.
Enlarging and reducing shapes on the Cartesian plane
Part A: Finding the image of a rectangle under an enlargement transformation
The diagram shows rectangle \(ABCD\) and its image \(A'B'C'D'\) under an enlargement transformation with the origin as the centre of enlargement.
-
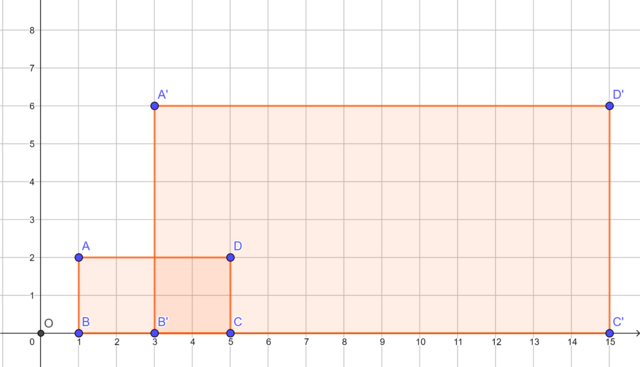
Compare the sides of rectangle \(ABCD\) and the corresponding sides of its image \(A'B'C'D'\):
- \[\dfrac{A'B'}{AB} = \dots\]
- \[\dfrac{B'C'}{BC} = \dots\]
- \[\dfrac{C'D'}{CD} = \dots\]
- \[\dfrac{D'A'}{DA} = \dots\]
- What do you notice about the ratios?
-
Compare the vertices of rectangle \(ABCD\) and the corresponding vertices of its image \(A'B'C'D'\).
- \(A = (\dots; \dots)\) and \(A' = (\dots; \dots)\)
- \(B = (\dots; \dots)\) and \(B' = (\dots; \dots)\)
- \(C = (\dots; \dots)\) and \(C' = (\dots; \dots)\)
- \(D = (\dots; \dots)\) and \(D' = (\dots; \dots)\)
- What do you notice about the values of the corresponding vertices?
- Calculate the perimeter of rectangle \(ABCD\) and the perimeter of rectangle \(A'B'C'D'\). What can you deduce?
- Complete the sentence: Perimeter of rectangle \(ABCD = \dots \times\) perimeter of rectangle \( A'B'C'D' \).
- Calculate the area of rectangle \(ABCD\) and the area of rectangle \(A'B'C'D'\). What can you deduce?
- Complete the sentence: Area of rectangle \(ABCD = \square^\square \times \) area of rectangle (\ A'B'C'D' \).
- How would you describe these two shapes? Are they congruent shapes? Are they similar shapes? Write a sentence to explain your answer.
Part B: Finding the image of a triangle under a reduction transformation
The diagram shows \(\triangle PQR\) and its image \(\triangle P'Q'R'\) under a reduction transformation with the origin as the centre of reduction.
-
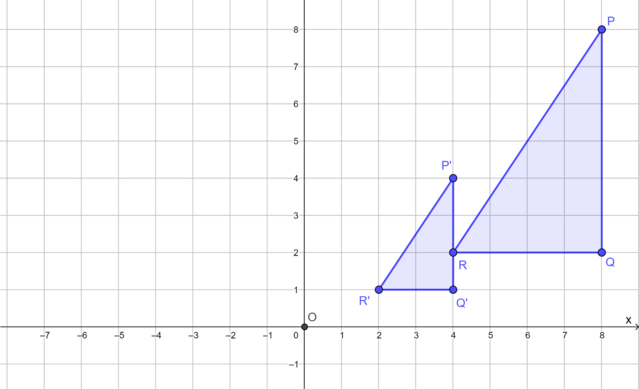
Compare the sides of \(\triangle PQR\) and the corresponding sides of its image \(\triangle P'Q'R'\):
- \[\dfrac{P'Q'}{PQ} = \dots\]
- \[\dfrac{Q'R'}{QR} = \dots\]
- \[\dfrac{R'P'}{RP} = \dots\] (Hint: Use the Theorem of Pythagoras)
- What do you notice about the ratios?
-
Compare the vertices of \(\triangle PQR\) and the corresponding vertices of its image \(\triangle P'Q'R'\).
- \(P = (\dots; \dots)\) and \(P' = (\dots; \dots)\)
- \(Q = (\dots; \dots)\) and \(Q' = (\dots; \dots)\)
- \(R = (\dots; \dots)\) and \(R' = (\dots; \dots)\)
- What do you notice about the values of the corresponding vertices?
- Calculate the perimeter of \(\triangle PQR\) and the perimeter of \(\triangle P'Q'R'\). What can you deduce?
- Complete the sentence: Perimeter of \(\triangle P'Q'R' = \dots \times\) perimeter of \(\triangle PQR\).
- Calculate the area of \(\triangle PQR\) and the area of \(\triangle P'Q'R'\). What can you deduce?
- Complete the sentence: Area of \(\triangle P'Q'R' = \left(\frac{\square}{\square} \right)^\square \times\) area of \(\triangle PQR\).
- How would you describe these two shapes? Are they congruent shapes? Are they similar shapes? Write a sentence to explain your answer.
Properties of enlargement and reduction transformations
We have discovered the following properties of enlargement and reduction transformations:
- All the sides of the image are scaled in the same proportion. This proportion is called the scale factor of the transformation.
- For enlargement and reduction transformations we must specify the centre of enlargement or reduction.
- For enlargement transformations, the scale factor is \(> 1\).
- For reduction transformations, the scale factor is a fraction between \(0\) and \(1\).
- When the centre of enlargement or reduction is the origin, the coordinates of the vertices of the image are scaled by the scale factor.
- Perimeter of the image = scale factor \(\times\) perimeter of the shape.
- Area of the image = (scale factor)\(^2 \times\) area of the shape
- For enlargement and reduction transformations, the shape and its image are similar shapes. Their shape and orientation are the same, but they differ in size.
Worked example 24.6: Determining the scale factor for an enlargement transformation
Determine the scale factor for the enlargement transformation with the origin as the centre of enlargement.
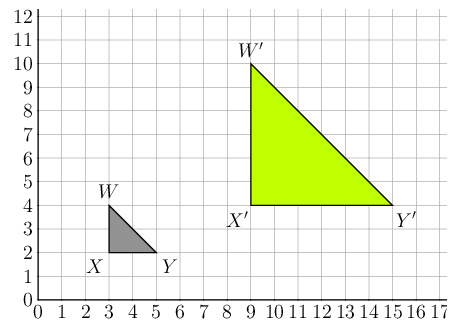
The diagram shows \(\triangle WXY\) and \(\triangle W'X'Y'\). We can draw dotted lines between the corresponding vertices to help us compare the corresponding sides.
Compare the lengths of the corresponding sides.
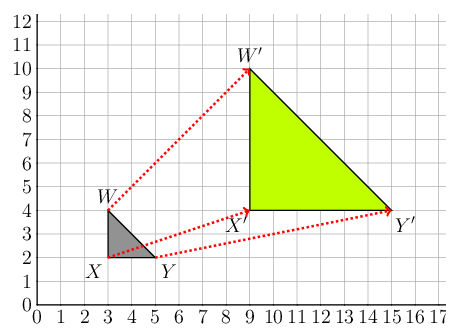
We can compare any pair of corresponding sides, so we choose sides for which we can easily find the lengths. \(XY\) and \(X'Y'\) are horizontal lengths and we can find the lengths by subtracting the values of the corresponding \(x\)-coordinates.
\[ \begin{align*} \frac{X'Y'}{XY} &= \frac{15 - 9}{5 - 3} \\ &= \frac{6}{2} \\ &= 3 \end{align*} \]We can calculate the lengths of the vertical sides \(XW\) and \(X'W'\) by subtracting the values of the corresponding \(y\)-coordinates.
\[ \frac{W'X'}{WX} = \frac{10 - 4}{4 - 2} = \frac{6}{2} = 3 \]We can find the length of \(WY\) and \(W'Y'\) using the Theorem of Pythagoras:
\[ \begin{align*} WY^2 &= WX^2 + XY^2 \\ &= (2)^2 + (2)^2 \\ &= 4 + 4 \\ &= 8 \\ WY &= \sqrt{8} \\ &= 2\sqrt{2} \end{align*} \] \[ \begin{align*} W'Y'^2 &= W'X'^2 + X'Y'^2 \\ &= (6)^2 + (6)^2 \\ &= 36 + 36 \\ &= 72 \\ W'Y' &= \sqrt{72} \\ &= 6\sqrt{2} \end{align*} \]So, \[\dfrac{W'Y'}{WY} = \dfrac{6\sqrt{2}}{2\sqrt{2}} = 3\]
Notice that the lengths of all three sides have been increased in the same proportion.
Write the final answer.
The scale factor for this enlargement transformation is 3.
Exercise 24.1
For each diagram, describe the enlargement or reduction transformation. Remember to state the centre of enlargement or reduction in each case.
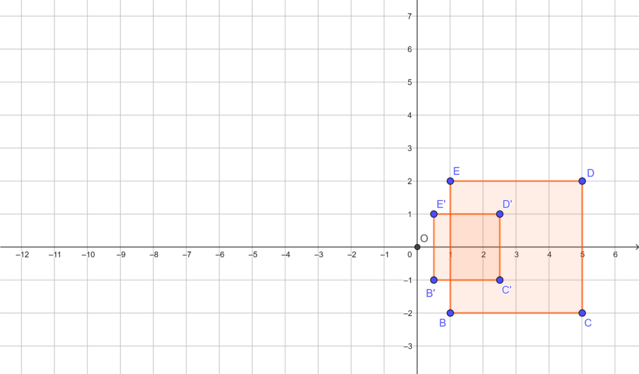
The diagram shows square \(BCDE\) and its image \(B'C'D'E'\) under a reduction transformation with the origin as the centre of reduction.
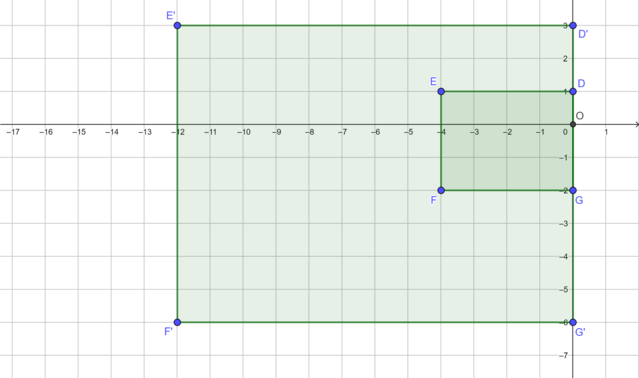
The diagram shows rectangle \(DEFG\) and its image \(D'E'F'G'\) under an enlargement transformation with the origin as the centre of enlargement.
The diagram shows \(\triangle PQR\) and its image \(\triangle P'Q'R'\) under a reduction transformation with the origin as the centre of reduction.
The diagram shows square \(QTSR\) and its image \(Q'T'S'R'\) under a reduction transformation with the origin as the centre of reduction. Find the scale factor.
Scale factor = \(\frac{1}{2}\)
The diagram shows \(\triangle ABC\) and its image \(\triangle A'B'C'\) under an enlargement transformation with the origin as the centre of enlargement. Determine the scale factor.
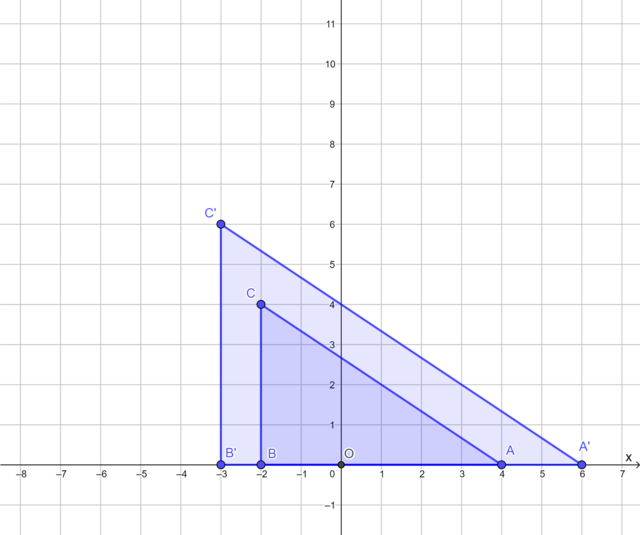
Scale factor = \(\frac{3}{2}\)
The diagram shows rectangle \(MNPQ\) and its image \(M'N'P'Q'\) under an enlargement transformation with the origin as the centre of enlargement. Find the scale factor.
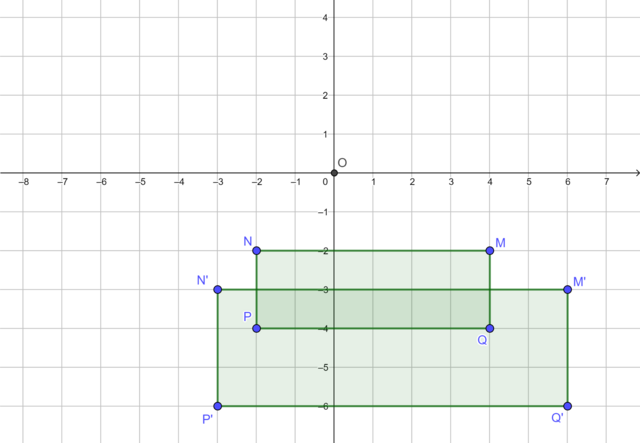
Scale factor = \(\frac{3}{2}\)
The diagram shows square \(WXYZ\) and its image \(W'X'Y'Z'\) under an enlargement transformation with the origin as the centre of enlargement. Find the scale factor.
Scale factor = 4