1.2 Ordering and comparing whole numbers
When writing whole numbers, you should pay careful attention to the place value of each digit in the number. This is especially important when you do calculations with whole numbers, because placing the digits incorrectly will cause errors.
Prime and composite numbers to \(100\)
A number that cannot be expressed as a product of two whole numbers, except as the product of \(1\) multiplied by the number itself, is called a prime number.
Composite numbers are natural numbers with more than two different factors. The sequence of composite numbers is \(4; 6; 8; 9; 10; 12; \ldots\)
For example, the number \(4\) can be expressed as \(4 \times 1\) or \(2 \times 2\). And the number \(12\) can be expressed as \(12 \times 1\) or \(6 \times 2\) or \(4 \times 3\).
- prime number
- a number that cannot be expressed as a product of two whole numbers, except for the product of \(1\) and the number itself.
- composite numbers
- natural numbers that have more than two different factors
- \(1\) is neither a prime number nor a composite number.
- \(1\) used to be a prime number, but mathematicians had to keep saying “all prime numbers except \(1\)”, so they changed this. \(1\) also can’t be a composite number, because its only factor is itself. So they decided to make \(1\) a special number in its own category.
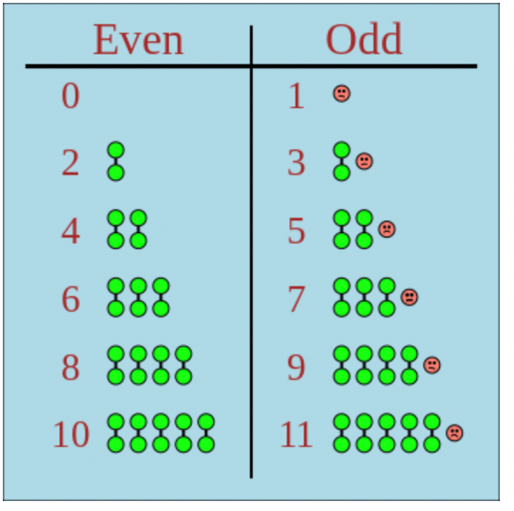
Even and odd numbers
Follow these rules to decide if each number is even, odd, or neither:
- If a whole number is divisible by \(2\), then it is even.
- If a whole number is not divisible by \(2\), then it is odd.
- If a number has a fractional part, then it cannot be even or odd.
Consecutive numbers
Consecutive means “next to each other” or “following each other without missing anything”.
For example, the list \({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}\) can be described as the list of consecutive whole numbers up to \(10\).
Sometimes, another property of numbers is used to clarify which consecutive numbers should be used. For example, if we need to decide whether a list of given numbers shows consecutive odd numbers or not, then we need to use the properties of odd numbers.
- Odd numbers start at \(1\) and count up in twos.
- So, consecutive odd numbers must start with an odd number and go up in twos, without skipping any numbers.
Similarly, the list of even numbers will start at \(2\) and count up in twos.
- So, consecutive even numbers start with an even number and go on in twos, without skipping any numbers.
Comparing numbers
We use a place value table to compare whole numbers. This is especially useful when working with big numbers. Place value tables let us look closely at what the digits in numbers mean. Digits in places further left represent bigger numbers.
Let’s compare the numbers, \(857\ 432\) and \(90\ 473\). First we will write them in a place value table.
| HTh \(100\ 000 \ \) |
TTh \(10\ 000 \ \) |
Th \(1\ 000 \ \) |
H \(100 \ \) |
T \(10 \ \) |
U \(1\) |
|---|---|---|---|---|---|
| \(9\) | \(0\) | \(4\) | \(7\) | \(3\) | |
| \(8\) | \(5\) | \(7\) | \(4\) | \(3\) | \(2\) |
The place value table helps us to see that \(857\ 432\) is bigger than \(90\ 473\). Another way of saying this is: \(90\ 473\) is smaller than \(857\ 432\).
We would write this mathematically as \(857\ 432 > 90\ 473\) or \(90\ 473 < 857\ 432\).
Worked Example 1.1: Comparing whole numbers
Compare these two numbers: \(631\ 947\) and \(632\ 035\). Explain the relationship between these two numbers using the correct inequality sign.
Use the place value table to organise the numbers.
| HTh \(100\ 000\) |
TTh \(10\ 000\) |
Th \(1\ 000\) |
H \(100\) |
T \(10\) |
U \(1\) |
|---|---|---|---|---|---|
| \(6\) | \(3\) | \(1\) | \(9\) | \(4\) | \(7\) |
| \(6\) | \(3\) | \(2\) | \(0\) | \(3\) | \(5\) |
Compare the digits starting at the left of the place value columns and moving to the right.
Starting on the left, both numbers have a \(6\) in the hundred thousands column. So, we need to look at the next column from the left: the ten thousands. These are also equal for both numbers! Looking at the thousands column, \(1 < 2\), so \(631\ 947\) is smaller than \(632\ 035\).
We write this as \(631\ 947 < 632\ 035\).
