1.3 Properties of whole numbers
The commutative property of addition and multiplication
We say that addition and multiplication are commutative. This means that the numbers can be swapped around, so their order does not change the answer.
- commutative property
- changing the order of the numbers does not change the answer
For example, the sum does not change if we swap around these numbers:
- \(5 + 10 = 15\) and \(10 + 5 = 15\)
- \(150 + 25 = 175\) and \(25 + 150 = 175\)
The same is true for multiplication:
- \(5 \times 8 = 40\) and \(8 \times 5 = 40\)
- \(10 \times 120 = 1\ 200\) and \(120 \times 10 = 1\ 200\)
This does not work for subtraction and division, however: \(8 - 4 \neq 4 - 8\) and \(6 \div 2 \neq 2 \div 6\). This also does not work for exponents: \(2^{3} \neq 3^{2}\). Can you see why the answers are not the same in each of these examples?
The associative (grouping) property of addition and multiplication
If three or more numbers must be multiplied, it does not matter which two of the numbers are multiplied first. In the same way, if three or more numbers must be added, it does not matter which two of the numbers are added first.
This is called the associative property of addition and multiplication. We can also say that addition and multiplication are associative.
- associative property
- when three or more numbers are added or multiplied, changing the order of the numbers does not change the answer
For example, the sum does not change if we group numbers together in different ways:
- \(4 + 7 + 5 + 6 = (4 + 7) + (5 + 6) = 11 + 11 = 22\)
- \(4 + 7 + 5 + 6 = (4 + 6) + (7 + 5) = 10 + 12 = 22\)
The same is true for multiplication:
- \(2 \times 12 \times 20 \times 3 = (2 \times 12) \times (20 \times 3) = 24 \times 60 = 1\ 440\)
- \(2 \times 12 \times 20 \times 3 = (2 \times 3) \times (12 \times 20) = 6 \times 240 = 1\ 440\)
Try to group the numbers differently. Do you get the same answer?
Let’s look at another example.
Lebogang and Nathi both must calculate \(25 \times 24\). They know that \(24 = 6 \times 4\).
- Lebogang calculates \(25 \times 4\) and then multiplies by \(6\).
- Nathi calculates \(25 \times 6\) and then multiplies by \(4\).
Will they get the same answer or not? Use your calculator to check:
- Lebogang: \(25 \times 4 \times 6 = 100 \times 6 = 600\)
- Nathi: \(25 \times 6 \times 4 = 150 \times 4 = 600\)
The distributive property of multiplication over addition and subtraction
The distributive property is a useful property because it allows us to do this:
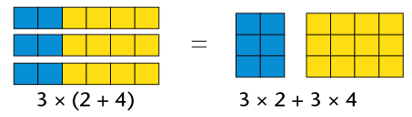
Both answers are \(18\). Notice that we must use brackets in the first example to show that the addition operation must be done first. Otherwise, we would have done the multiplication first.
For example, the expression \(3 \times 2 + 4\) means “multiply \(3\) by \(2\); then add \(4\)”. It does not mean “add \(2\) and \(4\); then multiply by \(3\)”.
The expression \(4 + 3 \times 2\) also means “multiply \(3\) by \(2\); then add \(4\)”.
If you wish to specify that addition or subtraction should be done first, that part of the expression should be enclosed in brackets.
The distributive property can be used to break up a difficult multiplication problem into smaller parts. For example, it can be used to make it easier to calculate \(6 \times 204\):
\(6 \times 204\) can be rewritten as \(6 \times (200 + 4)\) (Remember the brackets!)
\[\begin{align} 6 \times 204 &= 6 \times 200 + 6 \times 4 \\ &= 1\ 200 + 24 \\ &= 1\ 224 \end{align}\]Multiplication can also be distributed over subtraction. For example, to calculate \(7 \times 96\):
\[\begin{align} 7 \times 96 &= 7 \times (100 - 4) \\ &= 7 \times 100 - 7 \times 4 \\ &= 700 - 28 \\ &= 672 \end{align}\]We can write the distributive property of multiplication over addition and subtraction using formulas:
- \(a(b + c) = a \times b + a \times c\)
- \(a(b - c) = a \times b - a \times c\)
Worked Example 1.2: Applying the distributive properties of whole numbers
Use the distributive properties of multiplication to calculate \(8 \times 77\).
Rewrite \(77\) in tens and units.
\[77 = 70 + 7\]Use the distributive property.
The distributive property of multiplication over addition is:
\[a(b + c) = a \times b + a \times c\]So,
\[\begin{align} 8 \times 77 &= 8 \times (70 + 7) \\ &= 8 \times 70 + 8 \times 7 \end{align}\]Calculate the answer.
\[\begin{align} &8 \times 70 + 8 \times 7 \\ &= 560 + 56 \\ &= 616 \end{align}\]To multiply \(8\) by \(70\):
- multiply \(8\) by \(7\): \(8 \times 7 = 56\)
- multiply the answer by \(10\): \(56 \times 10 = 560\)
Worked Example 1.3: Applying the distributive properties of whole numbers
Use the distributive properties of multiplication to calculate \(6 \times 41\).
Rewrite \(41\) in tens and units.
\[41 = 40 + 1\]Use the distributive property.
The distributive property of multiplication over addition states that:
\[a(b + c) = a \times b + a \times c\]So,
\[\begin{align} 6 \times 41 &= 6 \times (40 + 1) \\ &= 6 \times 40 + 6 \times 1 \end{align}\]Calculate the answer.
\[\begin{align} &6 \times 40 + 6 \times 1 \\ &= 240 + 6 \\ &= 246 \end{align}\]To multiply \(6\) by \(40\):
- multiply \(6\) by \(4\): \(6 \times 4 = 24\)
- multiply the answer by \(10\): \(24 \times 10 = 240\)
Special properties when calculating with whole numbers
Think of an inverse operation as something that “reverses” another operation, or cancels it out.
-
Addition and subtraction as inverse operations
Addition and subtraction are inverses of each other. If you start with a number, then add and subtract the same number, the original number stays the same. For example, \(55 + 10 = 65\) and \(65 - 10 = 55\). So you are back to the original number after adding and subtracting \(10\).
-
Multiplication and division as inverse operations
Multiplication and division are inverses of each other. If you start with a number, then multiply and divide it by the same number, the original number stays the same. For example, \(15 \times 3 = 45\) and \(45 \div 3 = 15\). So you are back to the original number after multiplying and dividing by \(3\).
Numbers \(0\) and \(1\) also have important special properties that you need to remember when doing calculations.
-
The additive property of \(0\)
When we add zero to any number, the answer is that number.
-
The division property of \(0\)
Any number divided by \(0\) is undefined. For example, \(5 \div 0 =\) undefined (not possible to calculate).
-
The multiplicative property of \(0\)
Any number multiplied by \(0\) is \(0\). For example, \(15 \times 0 = 0\).
-
The multiplicative property of \(1\)
When we multiply any number by \(1\), the answer is that number. For example, \(36\ 500 \times 1 = 36\ 500\).
-
The division property of \(1\)
When dividing by \(1\), the answer remains the same. For example, \(135 \div 1 = 135\).
Be careful, \(1 \div 135 \neq 135\)!
Worked Example 1.4: Using the number \(1\) in addition
Calculate the following without using a calculator.
\[\frac{997 + 290}{997 + 290} + 251\]Look for a way to simplify your calculations.
The numerator and the denominator of the fraction are the same. When a number is divided by itself, the answer is always \(1\). So,
\[\frac{997 + 290}{997 + 290} = 1\]Calculate the final answer.
\[1 + 251 = 252\]Be careful when adding \(1\). This is not the same as multiplying by \(1\).
Worked Example 1.5: Using \(0\) in multiplication
Calculate the following without using a calculator.
\[929 - (224 + 124) \times 0\]Multiply first.
\[(224 + 124) \times 0\]We know that any number multiplied by \(0\) is always \(0\). So, it is not necessary to calculate inside the brackets. The answer of the multiplication will be \(0\).
\[348 \times 0 = 0\]Subtract.
\[929 - 0 = 929\]The number does not change when \(0\) is subtracted.
The final answer is \(929\).
