1.5 Multiples and factors
Let’s revise multiplication facts.
If \(n\) is a natural number, then \(2n\) represents the multiples of \(2\).
So, the numbers \(2; 4; 6; 8; 10; 12; 14; 16; 18; \ldots\) are multiples of \(2\).
In the same way, the numbers \(7; 14; 21; 28; 35; 42; 49; \ldots\) are multiples of \(7\).
When you need to answer the question: “Of which numbers is \(20\) a multiple?”, you look for factors of the number \(20\).
\(20\) is a multiple of \(1; 2; 4; 5; 10\) and \(20\), and all of these numbers are factors of \(20\).
Factors come in pairs. The following pairs are factors of \(20\):
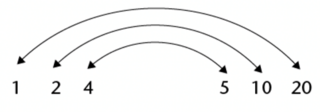
To find the factors
A natural number can be divided by its factors, without leaving a remainder. So, the factor of a natural number can divide that number perfectly without leaving a remainder. For example, \(2\) is one of the factors of \(14\), because \(14 \div 2 = 7\), with no remainder.
To find the multiples
The multiples of \(5\) are \(1 \times 5\), \(2 \times 5\), \(3 \times 5\), \(4 \times 5\), and so on. We call something a multiple of \(5\) if it is equal to \(5\) multiplied by another natural number. So, a multiple of any natural number is a value that is equal to the original number multiplied by another natural number. You can think of the multiples as the “times table” of the original number.
Worked Example 1.17: Finding multiples and factors
List all the factors of \(45\).
Find the first pair of factors.
To find the factors of a number, start by dividing by \(1\). We always get \(1\) and the number itself as factors of the number.
\(45 \div 1 = 45\) and \(45 \div 45 = 1\)
So, our first factor-pair is \(1\) and \(45\).
Continue with the next number until you find a factor.
\(2\) does not go into \(45\) without a remainder:
\[45 \div 2 = \text{22,5}\]So, \(2\) is not a factor of \(45\).
Next, let’s try dividing by \(3\).
\(45 \div 3 = 15\) and \(45 \div 15 = 3\)
So, our next factor-pair is \(3\) and \(15\).
\(4\) does not go into \(45\) without a remainder:
\[45 \div 4 = \text{11,25}\]So, \(4\) is not a factor of \(45\).
Continuing in this way, we get all of the factors of \(45\).
Next, let’s try dividing by \(5\).
\(45 \div 5 = 9\) and \(45 \div 9 = 5\)
So, our next factor-pair is \(5\) and \(9\).
List all the factors in numerical order.
\[1; 3; 5; 9; 15; 45\]Worked Example 1.18: Finding multiples and factors
List the first five multiples of \(45\).
List the first five multiples
The first five multiples of \(45\) are found by multiplying \(45\) by the first \(5\) natural numbers.
- \(1 \times 45 = 45\)
- \(2 \times 45 = 90\)
- \(3 \times 45 = 135\)
- \(4 \times 45 = 180\)
- \(5 \times 45 = 225\)
So, the first five multiples of \(45\) are \(45; 90; 135; 180; 225\).
Prime factors up to \(100\)
The number \(36\) can be written as \(2 \times 2 \times 3 \times 3\). Because \(2\) and \(3\) are used twice, they are called repeated factors of \(36\).
Remember, a number that cannot be expressed as a product of two whole numbers, except as the product the number itself, is called a prime number.
Composite numbers are natural numbers with more than two different factors. The sequence of composite numbers is \(4; 6; 8; 9; 10; 12; \ldots\)
Prime factorisation
To find all the factors of a number, you can write the number as the product of prime factors. First write it as the product of two convenient (composite) factors and then split these factors into smaller factors until all the factors are prime numbers. Then take all the possible combinations of the products of the prime factors.
Every composite number can be expressed as the product of prime factors, and this can happen in only one way.
For example: Find the factors of \(84\).
Write \(84\) as the product of prime factors by starting with different known factors:
\[\begin{align} 84 &= 4 \times 21 \\ &= 2 \times 2 \times 3 \times 7 \end{align}\]or
\[\begin{align} 84 &= 7 \times 12 \\ &= 7 \times 3 \times 4 \\ &= 7 \times 3 \times 2 \times 2 \end{align}\]or
\[\begin{align} 84 &= 2 \times 42 \\ &= 2 \times 6 \times 7 \\ &= 2 \times 2 \times 3 \times 7 \end{align}\]A more systematic way of finding the prime factors of a number would be to start with the prime numbers and try the consecutive prime numbers \(2; 3; 5; 7; \ldots\) as possible factors.
The work may be set out as shown below.
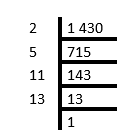
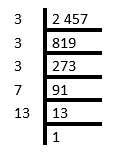
We can use exponents to write the products of prime factors more compactly as products of powers of prime factors.
- \(2\ 457 = 3 \times 3 \times 3 \times 7 \times 13 = 3^{3} \times 7 \times 13\)
- \(72 = 2 \times 2 \times 2 \times 3 \times 3 = 2^{3} \times 3^{2}\)
- \(1\ 500 = 2 \times 2 \times 3 \times 5 \times 5 \times 5 = 2^{2} \times 3 \times 5^{3}\)
This method is called the ladder method of factorisation.
- ladder method
- The ladder method is a way of finding the prime factors of a number. You divide the number by prime numbers,
until you get \(1\). The ladder method helps to organise the answer. Here is how to lay it out:
- Draw a vertical line.
- Write the original number to the right of the line.
- Find the smallest prime that divides into the number and write it to the left of the line.
- Do the division and write the answer below the starting number. If the answer is prime, stop. Otherwise, repeat steps three and four until you get \(1\) as your answer from the division.
Worked Example 1.19: Finding factors using prime factorisation
Find the factor-pairs of \(3\ 549\).
Find all the factors.

Write other factor-pairs.
\[3\ 549 = 3 \times (7 \times 13 \times 13) = 3 \times 1\ 183\]This shows that \(3\) and \(1\ 183\) are a factor-pair of \(3\ 549\).
Grouping differently will give the other pairs:
- \(3\ 549 = 7 \times (3 \times 13 \times 13) = 7 \times 507\) therefore \(7\) and \(507\)
- \(3\ 549 = 13 \times (3 \times 7 \times 13) = 13 \times 273\) therefore \(13\) and \(273\)
- \(3\ 549 = (7 \times 3) \times (13 \times 13) = 21 \times 169\) therefore \(21\) and \(169\)
- \(3\ 549 = (3 \times 13) \times (7 \times 13) = 39 \times 91\) therefore \(39\) and \(91\)
Lowest common multiples and highest common factors
Think about these questions:
- Is \(4 \times 5\) a multiple of \(4\)?
- Is \(4 \times 5\) a multiple of \(5\)?
The answer to both question is “Yes, \(4 \times 5\) is a multiple of both \(4\) and \(5\).”
The product of numbers is a multiple of each of the factors of the product. So, \(20\) is a multiple of \(4\) and it is also a multiple of \(5\).
We often use common multiples when fractions with different denominators are added.
For example, to add \(\frac{2}{3} + \frac{3}{4}\), we first find the common denominator which is \(3 \times 4\), so the sum becomes \(\frac{8}{12} + \frac{9}{12}\).
In the same way, we could use \(6 \times 8 = 48\) as a common denominator to add \(\frac{1}{6} + \frac{3}{8}\), but \(24\) is the lowest common multiple (LCM) of \(6\) and \(8\), so it is better to use that.
Prime factorisation makes it easy to find the lowest common multiple or highest common factor.
When we simplify a fraction, we divide the same number into the numerator and the denominator. For the simplest fraction, use the highest common factor (HCF) to divide into both numerator and denominator.
The HCF is divided into the numerator and the denominator to write the fraction in its simplest form.
So, \(\frac{36}{144} = \frac{2 \times 2 \times 3 \times 3}{2 \times 2 \times 2 \times 2 \times 3 \times 3} = \frac{1}{4}\)
Use prime factorisation to determine the LCM and HCF of \(32\), \(48\) and \(84\) in a systematic way:
- \(32 = 2 \times 2 \times 2 \times 2 \times 2 = 2^{5}\)
- \(48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^{4} \times 3\)
- \(84 = 2 \times 2 \times 3 \times 7 = 2^{2} \times 3 \times 7\)
The LCM is a multiple, so all of the factors of all the numbers must divide into it.
All of the factors that are present in the three numbers must also be factors of the LCM, even if it is a factor of only one of the numbers. But because it has to be the lowest common multiple, no unnecessary factors are in the LCM.
The highest power of each factor is in the LCM, because all of the other factors can divide into it. In \(32\), \(48\) and \(84\), the highest power of \(2\) is \(2^{5}\), the highest power of \(3\) is \(3\), and the highest power of \(7\) is \(7\).
\[\text{LCM } = 2^{5} \times 3 \times 7 = 672\]The HCF is a common factor. Therefore, for a factor to be in the HCF, it must be a factor of all of the numbers. \(2\) is the only number that appears as a factor of all three numbers. The lowest power of \(2\) is \(2^{2}\), so the HCF is \(2^{2}\).
Worked Example 1.20: Finding LCM and HCF
Determine the highest common factor (HCF) of \(150\) and \(1\ 260\), given that
- \(150 = 2 \times 3 \times 5 \times 5\)
- \(1\ 260 = 2 \times 2 \times 3 \times 3 \times 5 \times 7\)
Determine the factors that are common to both numbers.
The common factors are easier to see if we rewrite the numbers:
- \(150 = (2 \times 3 \times 5) \times 5\)
- \(1\ 260 = (2 \times 3 \times 5) \times 2 \times 3 \times 7\)
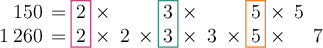
Find the highest common factor (HCF).
The highest common factor of \(150\) and \(1\ 260\) is \(2 \times 3 \times 5 = 30\).
Worked Example 1.21: Finding LCM and HCF
Determine the lowest common multiple (LCM) of \(150\) and \(1\ 260\), given that:
- \(150 = 2 \times 3 \times 5 \times 5\)
- \(1\ 260 = 2 \times 2 \times 3 \times 3 \times 5 \times 7\)
Write down the first few multiples of the bigger number.
- \(1\ 260 \times 1 = 1\ 260\)
- \(1\ 260 \times 2 = 2\ 520\)
- \(1\ 260 \times 3 = 3\ 780\)
- \(1\ 260 \times 4 = 5\ 040\)
- \(1\ 260 \times 5 = 6\ 300\)
Look at the multiples of the bigger number and check whether they are also multiples of the smaller number.
- \(1\ 260 \div 150 = \text{8,4}\)
- \(2\ 520 \div 150 = \text{16,8}\)
- \(3\ 780 \div 150 = \text{25,2}\)
- \(5\ 040 \div 150 = \text{33,6}\)
- \(6\ 300 \div 150 = 42\)
So, the lowest common multiple of \(150\) and \(1\ 260\) is \(6\ 300\).
- \(6\ 300 \div 150 = 42\)
- \(6\ 300 \div 1\ 260 = 5\)
