1.6 Solving problems with whole numbers
Order of operations
If you use “BODMAS” or “BEDMAS” correctly to remember the order of operations, you will get the same answer. But, evaluating an expression using terms will help more with algebra later on!
Worked Example 1.22: Using order of operations in calculations
Do not use a calculator. Follow the correct order of operations to find the answer.
\[7 - 2 \times 1 \times 3 + 3 \times 5\]Separate the terms of the expression.
Thinking about “terms” is a useful way to help us to simplify. Terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets. To evaluate an expression, we must:
- separate it into terms
- simplify each term (if needed)
- add or subtract from left to right.
This expression has three terms: \(7\), \(−2 \times 1 \times 3\), and \(+3 \times 5\). We must simplify the second and third terms.
\[7 - 2 \times 1 \times 3 + 3 \times 5 = 7 - 6 + 15\]Add and subtract from left to right
\[= 1 + 15 = 16\]Worked Example 1.23: Using order of operations in calculations
Do not use a calculator. Follow the correct order of operations to find the answer.
\[19 - (5 + 1^{2})\]Separate the expression into terms.
Remember that terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets. First separate into terms, then simplify, and then add or subtract from left to right.
This expression has three terms: \(19\), \(−5\), and \(+ 1^{2}\). We must simplify the exponent in the third term.
Simplify each term and calculate from left to right.
\[\begin{align} 19 - 5 + 1^{2} &= 19 - 5 + 1 \\ &= 14 + 1 \\ &= 15 \end{align}\]Rate
Instead of saying, for example “\(60\) calls per day”, people often say “at a rate of \(60\) calls per day”.
The word ‘per’ is often used to describe a rate and can mean for every, for, in each, in, out of, or every.
Speed is one example that describes the rate of movement over time. For example, a problem states that the invasive trees in the Western Cape are to be cut down in favour of natural vegetation. There are roughly \(3\ 000\ 000\) invasive trees in the area, and it is possible to cut them down at a rate of \(15\ 000\) trees per day with the labour available. The question could then be, “How many working days will it take before all the invasive trees have been cut down?”
To answer this rate question, you divide the total number of trees by the number that can be cut in one day:
\[3\ 000\ 000 \div 15\ 000 = 200\]So, it will take \(200\) days for all the trees to be cut down if the rate of cutting stays the same.
It is important to check that your answer makes sense. In this question we were looking for the number of days, so the answer must refer to days.
Worked Example 1.24: Solving problems with rate
A car travels a distance of \(180 \text{ km}\) in \(2\) hours on a straight road. How many kilometres can it travel in \(3\) hours at the same speed?
Understand the problem and summarise all the given information.
What we know:
- Distance = \(180 \text{ km}\)
- Time = \(2\) hours
- Speed = always the same
What we don’t know:
- Distance in \(3\) hours
Find the distance in \(1\) hour.
If the car travels \(180 \text{ km}\) in \(2\) hours, then it will travel \(180 \div 2 = 90 \text{ km}\) in \(1\) hour.
Find the distance in \(3\) hours (answer the question).
If the car travels \(90 \text{ km}\) in \(1\) hour, then it will travel \(90 \times 3 = 270 \text{ km}\) in \(3\) hours.
So, the car will travel \(270 \text{ km}\) in \(3\) hours.
Ratio
Another useful concept is that of ratio. When we talk about ratio, we compare different amounts, such as the number of green apples and red apples in a bag, or the number of adults and children in a group. We might say, “there are two green apples for every red apple in the bag”, or “there are two children for every adult in the group”.
- ratio
- a comparison of two (or more) quantities; we use ratios to show how many times more, or less, one quantity is than another
Look at these patterns.
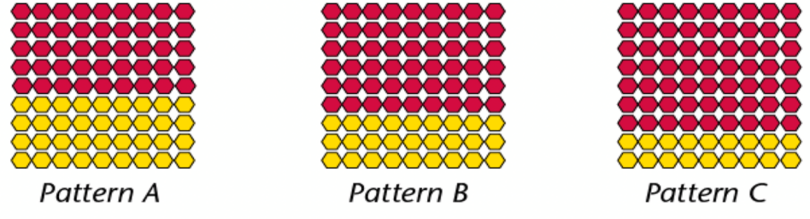
Imagine if these are the beads and we continue the same pattern. In pattern A in the picture, there are \(5\) red beads for every \(4\) yellow beads. Try to describe patterns B and C in the same way.
You can either start with red beads or the yellow beads. It is equally correct to say “In pattern A there are \(4\) yellow beads for every \(5\) red beads.”
The patterns in question 4 can be described like this: In pattern A, the ratio of yellow beads to red beads is \(4\) to \(5\). This is written as \(4 : 5\). In pattern B, the ratio between yellow beads and red beads is \(3 : 6\). In pattern C the ratio is \(2 : 7\).
When solving problems with ratio, first look for the total number of parts. For example, in the pattern above, there are two parts: red beads and yellow beads. Then work out each quantity according to the ratio.
Worked Example 1.25: Dividing amounts in the given ratio
If the number of hours that Nathi, Modi and Tim worked are in the ratio \(5 : 4 : 3\), then to be fair, the payment should also be shared in that ratio. What fraction of the payment should each person get?
Work out the number that represents the total of the parts of the ratio.
Add the parts of the ratio: \(5 + 4 + 3 = 12\)
Write the ratio of each person’s payment as a fraction.
Nathi should receive \(5\) parts, Modi \(4\) parts, and Tim \(3\) parts of the money. There are \(12\) parts altogether, so of the total payment:
- Nathi should receive \(\frac{5}{12}\),
- Modi should get \(\frac{4}{12}\),
- and Tim should get \(\frac{3}{12}\).
Increasing and decreasing ratio
Sometimes you need to increase a ratio. For example, to increase \(40\) in the ratio \(2 : 3\) means that the \(40\) represents two parts and must be increased so that the new number represents \(3\) parts. If \(40\) represents two parts, then \(20\) represents \(1\) part. The increased number will therefore be \(20 \times 3 = 60\).
Worked Example 1.26: Increasing a number in the given ratio
Increase \(56\) in the ratio \(2 : 5\).
Find the number that represents \(1\) part.
If \(56\) represents \(2\) parts, then \(56 \div 2 = 28\) represents \(1\) part.
Find the number that represent the unknown ratio.
The second number in the ratio is \(5\), so \(28 \times 5 = 140\).
So, the increased number is \(140\).
Check your answer.
If the answer is correct, then \(56 : 140 = 2 : 5\).
Simplifying the ratio on the left-hand side should give us the ratio on the right-hand side.
\[\left(56 \div \mathbf{28} \right) : \left(140 \div \mathbf{28} \right) = 2 : 5\]When simplifying the ratio, you look for the highest common factor of both numbers. In this example, \(28\) is the highest common factor of \(56\) and \(140\).
Worked Example 1.27: Decreasing a number in the given ratio
Decrease \(30\) in a ratio of \(2 : 3\).
We are decreasing in a ratio of \(2 : 3\), so the answer must be smaller than \(30\). Therefore, \(30\) must be equivalent to the bigger part of the ratio.
This new ratio should be equivalent to the original ratio. So, both sides should be multiplied or divided by the same whole number.
Find the number that represents \(1\) part.
If \(30\) represents \(3\) parts, then \(30 \div 3 = 10\) represents \(1\) part.
Find the number that represents the unknown ratio.
Our answer must be equivalent to the \(2\) part of the ratio.
\[2 \times 10 = 20\]Therefore, \(20 : 30\) is equivalent to \(2 : 3\).
\(30\) will decrease to \(20\).
