16.3 Conservation of charge
|
Previous
16.2 Two kinds of charge
|
Next
16.4 Quantisation of charge
|
16.3 Conservation of charge (ESAEU)
In all of the examples we've looked at charge was not created or destroyed but it moved from one material to another.
- Principle of conservation of charge
-
The principle of conservation of charge states that the net charge of an isolated system remains constant during any physical process, e.g. two charge objects making contacting and separating.
Conductors and insulators (ESAEV)
Some materials allow electrons to move relatively freely through them (e.g. most metals, the human body). These materials are called conductors.
Other materials do not allow the charge carriers, the electrons, to move through them (e.g. plastic, glass). The electrons are bound to the atoms in the material. These materials are called non-conductors or insulators.
The effect of the shape on the charge distribution is the reason that we only consider identical conductors for the sharing of charge.
If an excess of charge is placed on an insulator, it will stay where it is put and there will be a concentration of charge in that area of the object. However, if an excess of charge is placed on a conductor, the like charges will repel each other and spread out over the outside surface of the object. When two conductors are made to touch, the total charge on them is shared between the two. If the two conductors are identical, then each conductor will be left with half of the total net charge.
Arrangement of charge (ESAEW)
The electrostatic force determines the arrangement of charge on the surface of conductors. This is possible because charges can move inside a conductive material. When we place a charge on a spherical conductor the repulsive forces between the individual like charges cause them to spread uniformly over the surface of the sphere. However, for conductors with irregular shapes, there is a concentration of charge near the point or points of the object.
Notice in Figure 16.1 that we show a concentration of charge with more \(-\) or \(+\) signs, while we represent uniformly spread charges with uniformly spaced \(-\) or \(+\) signs.
This collection of charge can actually allow charge to leak off the conductor if the point is sharp enough. It is for this reason that buildings often have a lightning rod on the roof to remove any charge the building has collected. This minimises the possibility of the building being struck by lightning. This “spreading out” of charge would not occur if we were to place the charge on an insulator since charge cannot move in insulators.
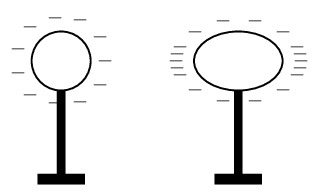
Figure 16.1: Charge on conductors
When two identical conducting spheres on insulating stands are allowed to touch they share the charge evenly between them. If the initial charge on the first sphere is \({Q}_{1}\) and the initial charge on the second sphere is \({Q}_{2}\), then the final charge on the two spheres after they have been brought into contact is:
\[Q = \frac{{Q}_{1} + {Q}_{2}}{2}\]|
Previous
16.2 Two kinds of charge
|
Table of Contents |
Next
16.4 Quantisation of charge
|
