16.4 Quantisation of charge
|
Previous
16.3 Conservation of charge
|
Next
Chapter summary
|
16.4 Quantisation of charge (ESAEX)
The basic unit of charge, called the elementary charge, e, is the amount of charge carried by one electron.
Unit of charge (ESAEY)
The charge on a single electron is \({q}_{e} = \text{1,6} \times \text{10}^{-\text{19}}\text{ C}\). All other charges in the universe consist of an integer multiple of this charge. This is known as charge quantisation.
\(Q = n{q}_{e}\)Charge is measured in units called coulombs (C). A coulomb of charge is a very large charge. In electrostatics we therefore often work with charge in micro-coulombs (\(\text{1}\) \(\text{μC}\)=\(\text{1} \times \text{10}^{-\text{6}}\) \(\text{C}\)) and nanocoulombs (\(\text{1}\) \(\text{nC}\)=\(\text{1} \times \text{10}^{-\text{9}}\) \(\text{C}\)).
In 1909 Robert Millikan and Harvey Fletcher measured the charge on an electron. This experiment is now known as Millikan's oil drop experiment. Millikan and Fletcher sprayed oil droplets into the space between two charged plates and used what they knew about forces and in particular the electric force to determine the charge on an electron.
Worked example 3: Charge quantisation
An object has an excess charge of \(-\text{1,92} \times \text{10}^{-\text{17}}\) \(\text{C}\). How many excess electrons does it have?
Analyse the problem and identify the principles
We are asked to determine a number of electrons based on a total charge. We know that charge is quantised and that electrons carry the base unit of charge which is \(-\text{1,6} \times \text{10}^{-\text{19}}\) \(\text{C}\).
Apply the principle
As each electron carries the same charge the total charge must be made up of a certain number of electrons. To determine how many electrons we divide the total charge by the charge on a single electron:
\begin{align*} N & = \frac{-\text{1,92} \times \text{10}^{-\text{17}}}{-\text{1,6} \times \text{10}^{-\text{19}}} \\ & = 120 \text{ electrons} \end{align*}Worked example 4: Conducting spheres and movement of charge
I have \(\text{2}\) charged metal conducting spheres on insulating stands which are identical except for having different charge. Sphere A has a charge of \(-\text{5}\) \(\text{nC}\) and Sphere B has a charge of \(-\text{3}\) \(\text{nC}\). I then bring the spheres together so that they touch each other. Afterwards I move the two spheres apart so that they are no longer touching.
-
What happens to the charge on the two spheres?
-
What is the final charge on each sphere?
Analyse the question
We have two identical negatively charged conducting spheres which are brought together to touch each other and then taken apart again. We need to explain what happens to the charge on each sphere and what the final charge on each sphere is after they are moved apart.
Identify the principles involved
We know that the charge carriers in conductors are free to move around and that charge on a conductor spreads itself out on the surface of the conductor.
Apply the principles
-
When the two conducting spheres are brought together to touch, it is as though they become one single big conductor and the total charge of the two spheres spreads out across the whole surface of the touching spheres. When the spheres are moved apart again, each one is left with half of the total original charge.
-
Before the spheres touch, the total charge is: \(-\text{5}\text{ nC} + (-\text{3}\text{ nC}) = -\text{8}\text{ nC}\). When they touch they share out the \(-\text{8}\) \(\text{nC}\) across their whole surface. When they are removed from each other, each is left with half of the original charge:
\[\frac{-\text{8}\text{ nC}}{2} = -\text{4}\text{ nC}\]on each sphere.
Worked example 5: Identical spheres sharing charge I
Two identical, insulated spheres have different charges. Sphere 1 has a charge of \(-\text{96} \times \text{10}^{-\text{18}}\) \(\text{C}\). Sphere 2 has \(\text{60}\) excess electrons. If the two spheres are brought into contact and then separated, what charge will each have?
Analyse the question
We need to determine what will happen to the charge when the spheres touch. They are insulators so we know they will NOT allow charge to move freely. When they touch nothing will happen.
Worked example 6: Identical spheres sharing charge II
Two identical, metal spheres on insulating stands have different charges. Sphere 1 has a charge of \(-\text{96} \times \text{10}^{-\text{18}}\) \(\text{C}\). Sphere 2 has \(\text{60}\) excess protons. If the two spheres are brought into contact and then separated, what charge will each have? How many electrons or protons does this correspond to?
Analyse the question
We need to determine what will happen to the charge when the spheres touch. They are metal spheres so we know they will be conductors. This means that the charge is able to move so when they touch it is possible for the charge on each sphere to change. We know that charge will redistribute evenly across the two spheres because of the forces between the charges. We need to know the charge on each sphere, we have been given one.
Identify the principles involved
This problem is similar to the earlier worked example. This time we have to determine the total charge given a certain number of protons. We know that charge is quantised and that protons carry the base unit of charge and are positive so it is \(\text{1,6} \times \text{10}^{-\text{19}}\) \(\text{C}\)
Apply the principles
The total charge will therefore be:
\begin{align*} {Q}_{2} & = 60\times \text{1,6} \times \text{10}^{-\text{19}}\text{ C} \\ & = \text{9,6} \times \text{10}^{-\text{18}}\text{ C} \end{align*}As the spheres are identical in material, size and shape the charge will redistribute across the two spheres so that it is shared evenly. Each sphere will have half of the total charge:
\begin{align*} Q& = \frac{{Q}_{1} + {Q}_{2}}{2} \\ & = \frac{\text{9,6} \times \text{10}^{-\text{18}}\text{ C} + \left(-\text{9,6} \times \text{10}^{-\text{18}}\text{ C}\right)}{2}\\ & = \text{0}\text{ C} \end{align*}So each sphere is now neutral.
No net charge means that there is no excess of electrons or protons.
Worked example 7: Conservation of charge
Two identical, metal spheres have different charges. Sphere 1 has a charge of \(-\text{9,6} \times \text{10}^{-\text{18}}\) \(\text{C}\). Sphere 2 has \(\text{30}\) excess electrons. If the two spheres are brought into contact and then separated, what charge will each have? How many electrons does this correspond to?
Analyse the problem
We need to determine what will happen to the charge when the spheres touch. They are metal spheres so we know they will be conductors. This means that the charge is able to move so when they touch it is possible for the charge on each sphere to change. We know that charge will redistribute evenly across the two spheres because of the forces between the charges. We need to know the charge on each sphere, we have been given one.
Identify the principles
This problem is similar to the earlier worked example. This time we have to determine the total charge given a certain number of electrons. We know that charge is quantised and that electrons carry the base unit of charge which is \(-\text{1,6} \times \text{10}^{-\text{19}}\) \(\text{C}\)
\begin{align*} {Q}_{2} & = 30 \times -\text{1,6} \times \text{10}^{-\text{19}}\text{ C}\\ & = -\text{4,8} \times \text{10}^{-\text{18}}\text{ C} \end{align*}Apply the principles: redistributing charge
As the spheres are identical in material, size and shape the charge will redistribute across the two spheres so that it is shared evenly. Each sphere will have half of the total charge:
\begin{align*} Q & = \frac{{Q}_{1} + {Q}_{2}}{2} \\ & = \frac{-\text{9,6} \times \text{10}^{-\text{18}} + \left(-\text{4,8} \times \text{10}^{-\text{18}}\right)}{2} \\ & = -\text{7,2} \times \text{10}^{-\text{18}}\text{ C} \end{align*}So each sphere now has \(-\text{7,2} \times \text{10}^{-\text{18}}\) \(\text{C}\) of charge.
We know that charge is quantised and that electrons carry the base unit of charge which is \(-\text{1,6} \times \text{10}^{-\text{19}}\) \(\text{C}\).
Apply the principles: charge quantisation
As each electron carries the same charge the total charge must be made up of a certain number of electrons. To determine how many electrons we divide the total charge by the charge on a single electron:
\begin{align*} N & = \frac{-\text{7,2} \times \text{10}^{-\text{18}}}{-\text{1,6} \times \text{10}^{-\text{19}}} \\ & = 45 \text{ electrons} \end{align*}The electroscope
The electroscope is a very sensitive instrument which can be used to detect electric charge. A diagram of a gold leaf electroscope is shown the figure below. The electroscope consists of a glass container with a metal rod inside which has 2 thin pieces of gold foil attached. The other end of the metal rod has a metal plate attached to it outside the glass container.
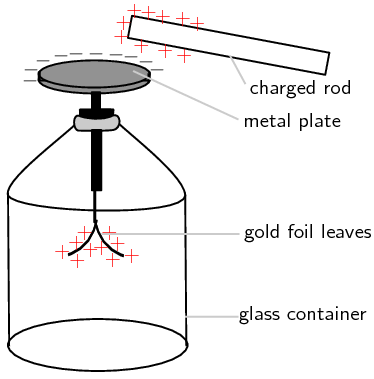
The electroscope detects charge in the following way: A charged object, like the positively charged rod in the picture, is brought close to (but not touching) the neutral metal plate of the electroscope. This causes negative charge in the gold foil, metal rod, and metal plate, to be attracted to the positive rod. Because the metal (gold is a metal too!) is a conductor, the charge can move freely from the foil up the metal rod and onto the metal plate. There is now more negative charge on the plate and more positive charge on the gold foil leaves. This is called inducing a charge on the metal plate. It is important to remember that the electroscope is still neutral (the total positive and negative charges are the same), the charges have just been induced to move to different parts of the instrument! The induced positive charge on the gold leaves forces them apart since like charges repel! This is how we can tell that the rod is charged. If the rod is now moved away from the metal plate, the charge in the electroscope will spread itself out evenly again and the leaves will fall down because there will no longer be an induced charge on them.
Grounding
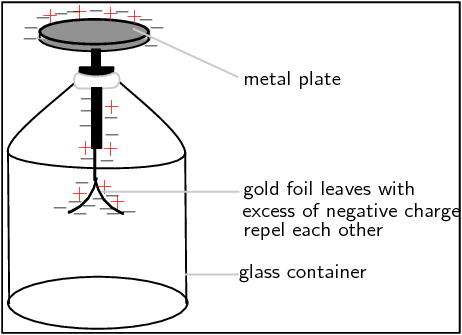
If you were to bring the charged rod close to the uncharged electroscope, and then you touched the metal plate with your finger at the same time, this would cause charge to flow up from the ground (the earth), through your body onto the metal plate. Connecting to the earth so charge flows is called
grounding
. The charge flowing onto the plate is opposite to the charge on the rod, since it is attracted to the charge on the rod. Therefore, for our picture, the charge flowing onto the plate would be negative. Now that charge has been added to the electroscope, it is no longer neutral, but has an excess of negative charge. Now if we move the rod away, the leaves will remain apart because they have an excess of negative charge and they repel each other. If we ground the electroscope again (this time without the charged rod nearby), the excess charge will flow back into the earth, leaving it neutral.
Polarisation (ESAEZ)
Unlike conductors, the electrons in insulators (non-conductors) are bound to the atoms of the insulator and cannot move around freely through the material. However, a charged object can still exert a force on a neutral insulator due to a phenomenon called polarisation.
If a positively charged rod is brought close to a neutral insulator such as polystyrene, it can attract the bound electrons to move round to the side of the atoms which is closest to the rod and cause the positive nuclei to move slightly to the opposite side of the atoms. This process is called polarisation. Although it is a very small (microscopic) effect, if there are many atoms and the polarised object is light (e.g. a small polystyrene ball), it can add up to enough force to cause the object to be attracted onto the charged rod. Remember, that the polystyrene is only polarised, not charged. The polystyrene ball is still neutral since no charge was added or removed from it. The picture shows a not-to-scale view of the polarised atoms in the polystyrene ball:

Some materials are made up of molecules which are already polarised. These are molecules which have a more positive and a more negative side but are still neutral overall. Just as a polarised polystyrene ball can be attracted to a charged rod, these materials are also affected if brought close to a charged object.
Electrostatic force
You can easily test that like charges repel and unlike charges attract each other by doing a very simple experiment.
Take a glass ball and rub it with a piece of silk, then hang it from its middle with a piece string so that it is free to move. If you then bring another glass rod which you have also charged in the same way next to it, you will see the ball on the string move away from the rod in your hand i.e. it is repelled.
If, however, you take a plastic rod, rub it with a piece of fur and then bring it close to the ball on the string, you will see the rod on the string move towards the rod in your hand i.e. it is attracted.



This happens because when you rub the glass with silk, tiny amounts of negative charge are transferred from the glass onto the silk, which causes the glass to have less negative charge than positive charge, making it positively charged.
. When you rub the plastic rod with the fur, you transfer tiny amounts of negative charge onto the rod and so it has more negative charge than positive charge on it, making it negatively charged.
Water is an example of a substance which is made of polarised molecules. If a positively charged rod, comb or balloon is brought close to a stream of water, the molecules can rotate so that the negative sides all line up towards the rod. The stream of water will then be attracted to the positively charged object since opposite charges attract.
Water being attracted to a charged balloon
|
Previous
16.3 Conservation of charge
|
Table of Contents |
Next
Chapter summary
|
