24.4 Translation transformations
Translating a point on the Cartesian plane
We can translate a point on the Cartesian plane from one position to another. For example, point \(A(1; 0)\) is translated 2 units to the right and 4 units upwards.
The position of point \(A\) after the transformation is called the image of \(A\) and we use the notation \(A'\) (we say "A prime").
- image
- the new position of a point, a line or an object after it has been transformed
\(A'\) is at \((3; 4)\).
\(A'\) is the image of \(A\) under a translation transformation.
Worked example 24.2: Translating a point on the Cartesian plane
Write down the coordinates of \(T'\) if \(T(2; 4)\) is translated \(3\) units to the left and \(2\) units downwards.
Complete the horizontal translation.
We move point \(T\) three units to the left (parallel to the \(x\)-axis). This translation moves \(T\) from the first quadrant to the second quadrant.
Write the final answer.
The coordinates of \(T'\) are \((-1; 2)\) and \(T'\) lies in the second quadrant.
Translating a shape on the Cartesian plane
We can translate a shape on the Cartesian plane from one position to another. For example:
- \(\triangle{ABC}\) is translated 2 units to the left and 2 units downwards
- \(\triangle{A'B'C'}\) is the image of \(\triangle{ABC}\) under a translation transformation.
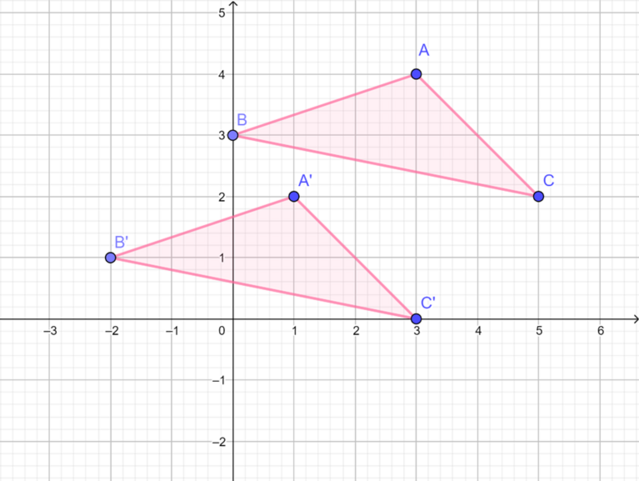
Notice that each vertex of \(\triangle{ABC}\) has been transformed by the same rule: slide 2 units to the left and 2 units downwards.
We can express this transformation rule as:
\[(x; y) \rightarrow (x - 2; y - 2)\]This is called a mapping notation.
- mapping notation
- a representation of the rule that relates every point on the shape to the corresponding point on the image
Finding the image of a rectangle under a translation transformation
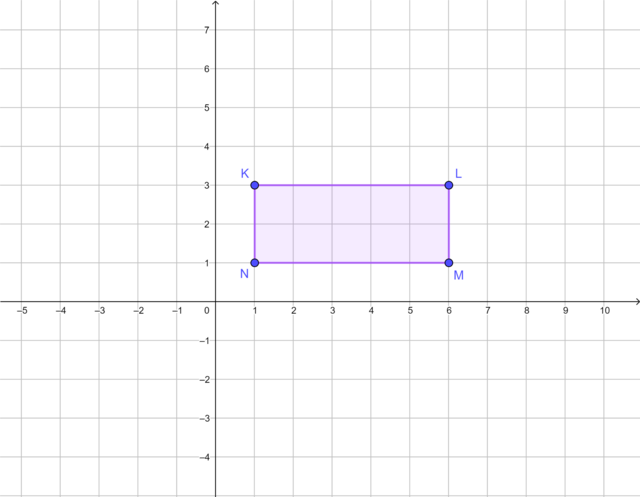
The diagram shows rectangle \(KLMN\) on the Cartesian plane.
-
Draw a copy of rectangle \(KLMN\) on a Cartesian plane.
-
Draw \(K'L'M'N'\), the image of \(KLMN\), translated 3 units to the right and 2 units upwards.
-
Express this translation transformation in mapping notation.
-
Compare the length of the corresponding sides of rectangle \(KLMN\) and rectangle \(K'L'M'N'\). What do you notice?
-
Compare the size of the corresponding interior angles of rectangle \(KLMN\) and rectangle \(K'L'M'N'\). What do you notice?
-
How would you describe these two shapes? Are they congruent shapes or similar shapes?
-
Calculate the perimeter of rectangle \(KLMN\) and the perimeter of rectangle \(K'L'M'N'\).
-
Calculate the area of rectangle \(KLMN\) and the area of rectangle \(K'L'M'N'\).
-
A translation transformation produces congruent shapes which have the same area and the same perimeter. Is this statement true or false?
Worked example 24.3: Translating a triangle on the Cartesian plane
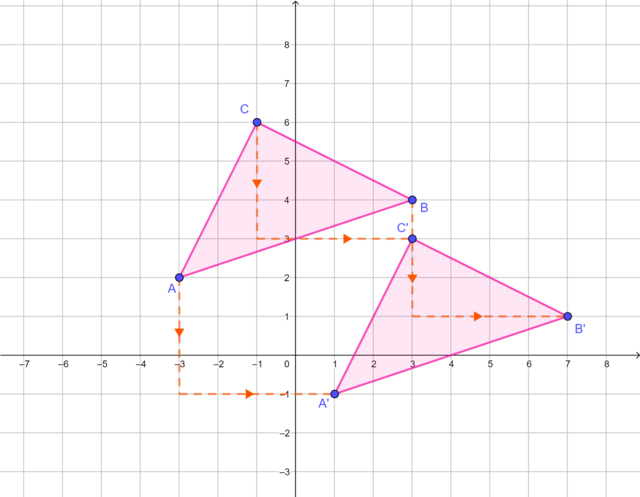
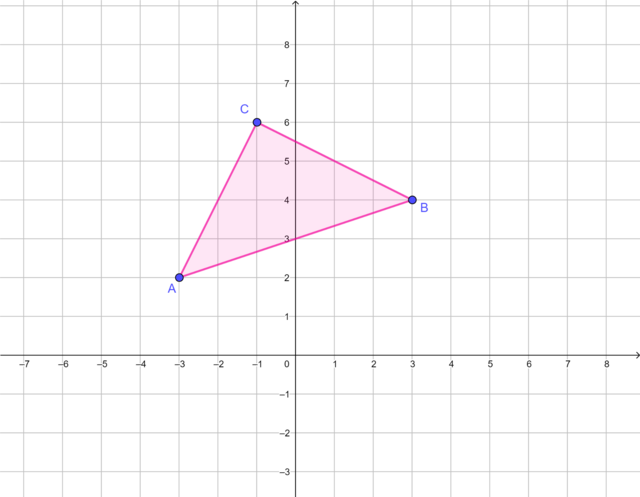
- Draw \(\triangle ABC\) with vertices \(A(-3; 2)\), \(B(3; 4)\) and \(C(-1; 6)\) on the Cartesian plane.
- Draw \(\triangle A'B'C'\), the image of \(\triangle ABC\), translated 4 units to the right and 3 units downwards.
- Write down the coordinates of the vertices \(A'\), \(B'\) and \(C'\).
- Express this translation transformation in mapping notation.
Draw the triangle on the Cartesian plane.
Translate each vertex of the triangle.
Translate each vertex of the \(\triangle ABC\) 4 units to the right and 3 units downwards to get the image \(\triangle A'B'C'\).