14.2 Ordering, comparing and place value of
decimal fractions
Decimal fraction notation
Decimal fractions and common fractions are simply different ways of expressing the same
number. We call them different notations.
- decimal fraction
- a decimal fraction is a fraction in which the digits of the numerator are written after a decimal point
To write a common fraction as a decimal fraction, we must first express the common fraction using a power of
ten (\(10\), \(100\), \(1\ 000\), etc.) as the denominator. For example:
\[\begin{align}
\frac{9}{20} &= \frac{9}{20} \times \frac{5}{5} \\
&= \frac{45}{100} \\
&= \text{0,45}
\end{align}\]
You can also use a calculator to divide the numerator by the denominator to get the decimal form of a fraction,
for example:
\[\begin{align}
\frac{9}{20} &= 9 \div 20 \\
&= \text{0,45}
\end{align}\]
To write a decimal fraction as a common fraction, we must first express it as a common fraction with a power of
ten as denominator, and then simplify the fraction if necessary. For example:
\[\begin{align}
\text{0,65} &= \frac{65}{100} \\
&= \frac{65 \div 5}{100 \div 5} \\
&= \frac{13}{20}
\end{align}\]
Place value
Each digit in the number has its own place value. For example, in the number \(\text{1,23}\), the
digit “\(3\)” is in the second decimal place. The second place is called the “hundredths
place”.
- place value
- the value of a digit according to its position in a number
For decimal fractions, the place values we work with are \(\frac{1}{10}\), \(\frac{1}{100}\), \(\frac{1}{1\
000}\) and \(\frac{1}{10\ 000}\). They are called tenths, hundredths, thousandths and ten thousandths.
These place values are represented from biggest to smallest, moving to the right after the decimal comma:
| units (U) |
, |
tenths (t) |
hundredths (h) |
thousandths (th) |
ten thousandths (tth) |
| \(1\) |
, |
\(\frac{1}{10}\) |
\(\frac{1}{100}\) |
\(\frac{1}{1\ 000}\) |
\(\frac{1}{10\ 000}\) |
The fractions for these place values are written in this way:
- \(\text{0,1}\) means zero units and one \(\frac{1}{10}\)
- \(\text{0,01}\) means zero units, zero tenths and one \(\frac{1}{100}\)
- \(\text{0,001}\) means zero units, zero tenths, zero hundredths and one \(\frac{1}{1\ 000}\)
- \(\text{0,0001}\) means zero units, zero tenths, zero hundredths, zero thousandths and one \(\frac{1}{10\ 000}\).
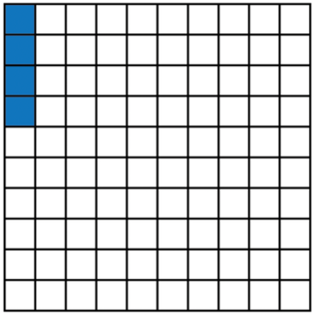
In the same way as for whole numbers, we move to a new place value each time we reach \(10\). For example, this
block of squares is divided into \(100\) parts.
One hundredth, which is \(\frac{1}{100} = \text{0,01}\), may be shown like this:
Four parts of this block of \(100\) squares, which is \(4 \times \frac{1}{100} = \frac{4}{100} = \text{0,04}\), may be
shown like this:
Worked Example 14.1: Finding place value in
decimal numbers
Write the place values of all the non-zero digits in the following number: \(\text{73 025,048}\)
Write the number in a place
value table. Show the decimal point clearly.
TTh
\((\text{10 000})\) |
Th
\((\text{1 000})\) |
H
\((\text{100})\) |
T
\((\text{10})\) |
U
\((\text{1})\) |
, |
t
\((\text{0,1})\) |
h
\((\text{0,01})\) |
th
\((\text{0,001})\) |
tth
\((\text{0,0001})\) |
| \(7\) |
\(3\) |
\(0\) |
\(2\) |
\(5\) |
, |
\(0\) |
\(4\) |
\(8\) |
|
Multiply each non-zero digit by the
value of the column it is in.
-
\(7 \times 10\ 000 = 70\ 000\)
-
\(3 \times 1\ 000 = 3\ 000\)
-
\(2 \times 10 = 20\)
-
\(5 \times 1 = 5\)
-
\(4 \times \text{0,01} = \text{0,04}\)
-
\(8 \times \text{0,001} = \text{0,008}\)
As you can see, we do not give the place value of the zeroes in a number, because \(0\) multiplied by
anything equals \(0\). So, the place value of any \(0\) will always be \(0\).
The zeroes have to be included in a number to show the place values of the other digits. This is why we
call \(0\) a placeholder.
When comparing decimal numbers, you can place them on the same place value table and compare the digits from
left to right. For example, to compare \(\text{36 601,25}\) with \(\text{36 705,75}\) we can place these numbers in the
table and compare the digits:
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 3 |
6 |
6 |
0 |
1 |
, |
2 |
5 |
|
|
| 3 |
6 |
7 |
0 |
5 |
, |
7 |
5 |
|
|
The hundred digits are different: \(6 < 7\). So the first decimal number is smaller than the second:
\(\text{36 601,25} < \text{36 705,75}\). We do not need to compare the digits that follow.
The number with fewer digits before the decimal comma is always smaller, so \(\text{999,99} < \text{1 111,11}\).
Exercise 14.1
Write down the place value of the given digit in each case.
- Give the values of the digits \(5\) and \(8\) in the number \(\text{5 021,08}\).
- Give the values of the digits \(1\) and \(4\) in the number \(\text{75,1804}\).
- Give the values of the digits \(9\) and \(7\) in the number \(\text{10 591,073}\).
- Give the two values of the digit \(5\) in the number \(\text{30 502,51}\).
- Give the three values of the digit \(9\) in the number \(\text{99 178,95}\).
-
The digits \(5\) and \(8\) in the number \(\text{5 021,08}\):
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
|
5 |
0 |
2 |
1 |
, |
0 |
8 |
|
|
-
\(5 \times 1\ 000 = \text{5 000}\)
-
\(8 \times \text{0,01} = \text{0,08}\)
-
The digits \(1\) and \(4\) in the number \(\text{75,1804}\):
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
|
|
|
7 |
5 |
, |
1 |
8 |
0 |
4 |
-
\(1 \times \text{0,1} = \text{0,1}\)
-
\(4 \times \text{0,0001} = \text{0,0004}\)
-
The digits \(9\) and \(7\) in the number \(\text{10 591,073}\):
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 1 |
0 |
5 |
9 |
1 |
, |
0 |
7 |
3 |
|
-
\(9 \times 10 = 90\)
-
\(7 \times \text{0,01} = \text{0,07}\)
-
The two values of the digit \(5\) in the number \(\text{30 502,51}\):
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 3 |
0 |
5 |
0 |
2 |
, |
5 |
1 |
|
|
-
\(5 \times 100 = 500\)
-
\(5 \times \text{0,1} = \text{0,5}\)
-
The three values of the digit \(9\) in the number \(\text{99 178,95}\):
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 9 |
9 |
1 |
7 |
8 |
, |
9 |
5 |
|
|
-
\(9 \times 10\ 000 = 90\ 000\)
-
\(9 \times 1\ 000 = 9\ 000\)
-
\(9 \times \text{0,1} = \text{0,9}\)
Compare the following decimal numbers.
- \(\text{77 601,5}\) and \(\text{77 599,9}\)
- \(\text{98 713,41}\) and \(\text{99 100,99}\)
- \(\text{0,543}\) and \(\text{10,599}\)
- \(\text{32 100,51}\) and \(\text{32 100,59}\)
-
\(\text{77 601,5}\) and \(\text{77 599,9}\)
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 7 |
7 |
6 |
0 |
1 |
, |
5 |
|
|
|
| 7 |
7 |
5 |
9 |
9 |
, |
9 |
|
|
|
In the hundreds place, \(6 > 5\), so \(\text{77 601,5} > \text{77 599,9}\).
-
\(\text{98 713,41}\) and \(\text{99 100,99}\)
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 9 |
8 |
7 |
1 |
3 |
, |
4 |
1 |
|
|
| 9 |
9 |
1 |
0 |
0 |
, |
9 |
9 |
|
|
In the thousands place \(8 < 9\), so \(\text{98 713,41} < \text{99 100,99}\).
-
\(\text{0,543}\) and \(\text{10,599}\)
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
|
|
|
|
0 |
, |
5 |
4 |
3 |
|
|
|
|
1 |
0 |
, |
5 |
9 |
9 |
|
\(\text{0,543}\) has only one digit before the comma, so \(\text{0,543} < \text{10,599}\)
-
\(\text{32 100,51}\) and \(\text{32 100,59}\)
TTh
(\(\text{10 000}\)) |
Th
(\(\text{1 000}\)) |
H
(\(\text{100}\)) |
T
(\(\text{10}\)) |
U
(\(\text{1}\)) |
, |
t
(\(\text{0,1}\)) |
h
(\(\text{0,01}\)) |
th
(\(\text{0,001}\)) |
tth
(\(\text{0,0001}\)) |
| 3 |
2 |
1 |
0 |
0 |
, |
5 |
1 |
|
|
| 3 |
2 |
1 |
0 |
0 |
, |
5 |
9 |
|
|
In the hundredths place \(1 < 9\), so \(\text{32 100,51} < \text{32 100,59}\).
Number lines
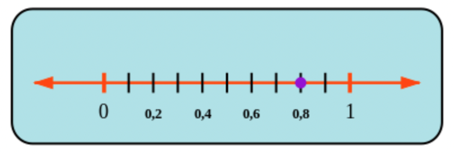
Decimal numbers work by dividing things into tens. The vertical indicators on the number line in the diagram
below divide the space from zero to one into \(10\) parts. These indicators represent the numbers \(\text{0,1}\) and
then \(\text{0,2}\) and \(\text{0,3}\), and so on until you get to \(1\).
The scale on the number line is \(\text{0,2}\), so some numbers are skipped. For example, \(\text{0,3}\) is at the indicator
between \(\text{0,2}\) and \(\text{0,4}\).
The dot is on the number \(\text{0,8}\).
You can also think of this number as a fraction, which is \(\frac{8}{10}\) because the picture shows \(8\)
parts out of \(10\).
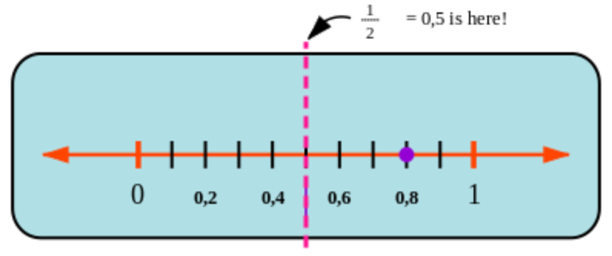
The number line is useful for comparing decimal numbers. For example, the diagram below shows the position of
\(\text{0,5}\) (a half) on the number line. You can see that \(\text{0,8}\) is more (bigger) than \(\text{0,5}\). We can write this
as an inequality: \(\text{0,8} > \text{0,5}\).
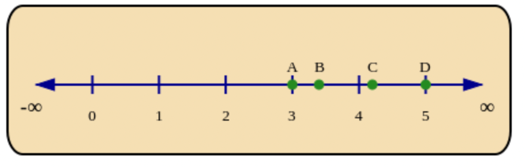
When there are more decimals to compare, placing them in order on the number line helps you to find the answer:
There are four numbers marked with dots on the number line below. The points are labelled \(A\), \(B\), \(C\)
and \(D\).
You can easily see that \(A < B < C < D\).
Now if you were given decimal numbers: \(\text{3,4}; \text{5,0}; \text{4,2}; \text{3,0}\), you could check their position on the number
line and place them in order from smallest to biggest.
\[\begin{align}
A &= \text{3,0} \\
B &= \text{3,4} \\
C &= \text{4,2} \\
D &= \text{5,0}
\end{align}\]
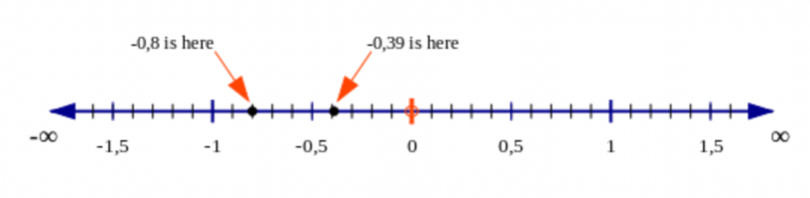
If we extend the number line in the negative direction, then we can also compare negative decimal numbers.
Remember, a positive number is always greater than a negative number, and zero is in between the positives
and negatives! For example, \(- \text{0,8} < \text{0,39}\).
If both numbers are negative, then the number further to the left on the number line is smaller. For example,
\(- \text{0,8} < - \text{0,39}\).